R言語による時系列予測とクロスバリデーション法による評価
時系列データへのクロスバリデーション法を用いて、予測精度の評価を行う方法を説明します。
R言語のforecastパッケージのtsCV関数を用いると、効率的な短いコードで実装が可能です。
この記事では、時系列データの前処理~モデル化~予測~予測の評価、といった一連の流れをすべて通して解説します。
今回は標準的な時系列モデルであるSARIMAモデルを用いますが、このモデル以外でもおおよその手順は変わらないと思います。
予測の評価における基本的な事項は『予測の評価方法:誤差の指標とナイーブな予測』も合わせて参照してください。
コードはGitHubから参照することができます。
スポンサードリンク
目次
- 分析の準備と前処理
- SARIMAモデルの構築
- SARIMAによる予測
- テストデータを使った予測の評価
- クロスバリデーション法による予測の評価
- スライド型のクロスバリデーション法の実行
- 後記
1.分析の準備と前処理
この記事では、時系列データの前処理~モデル化~予測~予測の評価、といった一連の流れをすべて通して解説します。
逆に言えば、時系列データを予測するというだけでも、まじめにやればこれだけの手順を踏まなければいけないということですね。
この記事の方針は以下の通りです。
1.前処理としては、データの対数変換を行います。
2.モデル化としては、SARIMAモデルを構築します。
3.予測は、forecastパッケージの関数を使えば素直なコードで実行できます。
4.予測の評価としては以下の3つを行います
4-1.訓練データとテストデータに分けて、テストデータでの予測精度を評価する
4-2.訓練データを1時点ずつ増やしていき、予測を何度も行い、その時の予測精度を評価する
4-3.訓練データをスライドさせていき、予測を何度も行い、その時の予測精度を評価する
まずは、分析に必要なパッケージを読み込みます。
必要であれば1~3行目のコメントを外して、パッケージをインストールしてください。
分析に使うのは主にforecastパッケージです。グラフを描くために残りのパッケージを読み込んでおきました。
# install.packages("forecast")
# install.packages("ggfortify")
# install.packages("ggplot2")
# install.packages("gridExtra")
library(forecast)
library(ggfortify)
library(ggplot2)
library(gridExtra)
続いて、データの読み込みと対数変換です。
今回は飛行機乗客数のデータを使いました。月単位のデータです。R言語における標準的な時系列データのクラスであるts型で保存されています。
> # 対象データ > # Monthly Airline Passenger Numbers 1949-1960 > # 対数変換したものを使う > log_air_pass <- log(AirPassengers) > class(log_air_pass) [1] "ts"
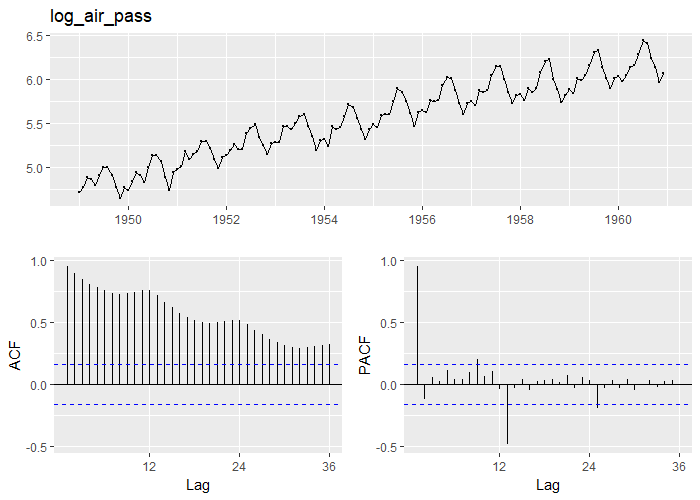
データを読み込んだら、最初にやることは図示です。
以下の1行のコードで美麗なグラフが描けます。ACFは自己相関でPACFは偏自己相関と呼ばれる指標です。例えば『時系列解析_理論編』等を参照してください。
# 図示 ggtsdisplay(log_air_pass)
実際に数値を眺めて、どんなデータなのか確認をしておきます。
> # データの確認
> print(log_air_pass, digits = 4)
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949 4.718 4.771 4.883 4.860 4.796 4.905 4.997 4.997 4.913 4.779 4.644 4.771
1950 4.745 4.836 4.949 4.905 4.828 5.004 5.136 5.136 5.063 4.890 4.736 4.942
1951 4.977 5.011 5.182 5.094 5.147 5.182 5.293 5.293 5.215 5.088 4.984 5.112
1952 5.142 5.193 5.263 5.198 5.209 5.384 5.438 5.489 5.342 5.252 5.147 5.268
1953 5.278 5.278 5.464 5.460 5.434 5.493 5.576 5.606 5.468 5.352 5.193 5.303
1954 5.318 5.236 5.460 5.425 5.455 5.576 5.710 5.680 5.557 5.434 5.313 5.434
1955 5.489 5.451 5.587 5.595 5.598 5.753 5.897 5.849 5.743 5.613 5.468 5.628
1956 5.649 5.624 5.759 5.746 5.762 5.924 6.023 6.004 5.872 5.724 5.602 5.724
1957 5.753 5.707 5.875 5.852 5.872 6.045 6.142 6.146 6.001 5.849 5.720 5.817
1958 5.829 5.762 5.892 5.852 5.894 6.075 6.196 6.225 6.001 5.883 5.737 5.820
1959 5.886 5.835 6.006 5.981 6.040 6.157 6.306 6.326 6.138 6.009 5.892 6.004
1960 6.033 5.969 6.038 6.133 6.157 6.282 6.433 6.407 6.230 6.133 5.966 6.068
>
> # サンプルサイズ
> length(log_air_pass)
[1] 144
>
> # 何年あるか?
> length(log_air_pass) / 12
[1] 12
最後に、訓練データとテストデータに分割しておきます。
ts型のデータの場合は、window関数の引数にstartやendと指定することで簡単にデータの切り出しが可能です。
# 訓練データとテストデータに分割 # 最初の10年を訓練、最後の2年をテストデータとする train <- window(log_air_pass, end=c(1958, 12)) test <- window(log_air_pass, start=c(1959, 1))
2.SARIMAモデルの構築
SARIMAモデルを構築します。
forecastパッケージのauto.arima関数を使うことで、ほぼ自動的に次数の選択やモデルの構築が完了します。
auto.arima関数の使い方に関しては『ARIMAモデルによる株価の予測』等も参照してください。
# モデルを作る
mod_sarima <- auto.arima(train,
ic = "aic",
stepwise = F,
parallel = TRUE,
num.cores = 4)
推定結果を出力します。
ARIMA(0,1,1)(0,1,1)が選択されたようです。
> mod_sarima
Series: train
ARIMA(0,1,1)(0,1,1)[12]
Coefficients:
ma1 sma1
-0.3424 -0.5405
s.e. 0.1009 0.0877
sigma^2 estimated as 0.001432: log likelihood=197.51
AIC=-389.02 AICc=-388.78 BIC=-381
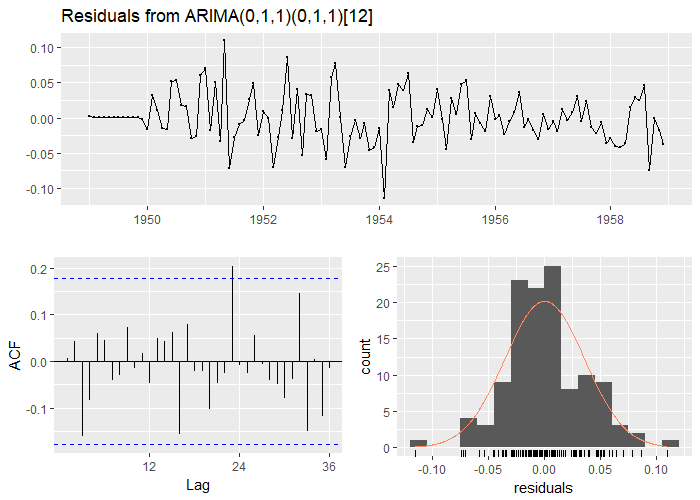
残差のチェックを行います。
checkresiduals関数を使うと、残差の自己相関の検定と残差の図示を同時に行ってくれます。
結果を見ると『p-value = 0.5618』となっているので有意な自己相関は見られず、残差のグラフを見ても大きな問題は見当たらなかったのでそのまま進めます。
> # 残差の評価 > checkresiduals(mod_sarima) Ljung-Box test data: Residuals from ARIMA(0,1,1)(0,1,1)[12] Q* = 20.34, df = 22, p-value = 0.5618 Model df: 2. Total lags used: 24
スポンサードリンク
3.SARIMAによる予測
推定されたモデルを用いて、予測を行います。
予測はforecastパッケージのforecast関数を使います。
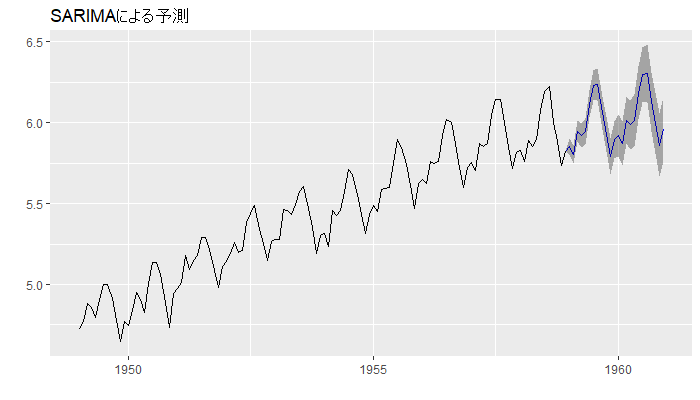
予測結果を『f_sarima』という変数に格納したうえで、図示を行います。
コードと結果をまとめて載せます。
# 予測期間 h <- length(test) # 予測 f_sarima <- forecast(mod_sarima, h = h) # 予測結果の図示 autoplot(f_sarima, main = "SARIMAによる予測")
4.テストデータを使った予測の評価
予測の評価はaccuracy関数を使うことで簡単に実行できます。
accuracy関数に関しては『予測の評価方法:誤差の指標とナイーブな予測』も合わせて参照してください
> # 予測の評価
> accuracy(f_sarima, test)
ME RMSE MAE MPE MAPE MASE ACF1 Theil's U
Training set -0.0001250111 0.03539809 0.02640383 -0.0003836216 0.4867206 0.2145046 0.005834845 NA
Test set 0.0895992058 0.09593236 0.08959921 1.4634770472 1.4634770 0.7279033 0.327959306 0.8735145
例えばRMSEの値を見ると、訓練データでは0.03539809、テストデータでは0.09593236となりました。
しかし、0.09といった数値を見て「なるほど!」と思う方はあまりいないのではないかと思います。
RMSEは誤差の大きさですので、小さければ小さい方が良いのですが、どれくらい小さければ十分なのでしょうか。目安がほしいところですね。
そこで「複雑な技術を使わなくても行うことができる予測」すなわち「ナイーブ予測」を用います。
ナイーブ予測のRMSEと、頑張って構築したSARIMAモデルのRMSEを比較して、SARIMAモデルの方が小さければ、十分に良い予測ができていると判断できます。
ナイーブ予測の種類に関してはやはり『予測の評価方法:誤差の指標とナイーブな予測』も参照していただければと思いますが、今回は以下の3つのタイプのナイーブ予測を用いることにします。
1.訓練データの最終時点を予測値とする
2.1にたいして、全体のトレンド(今回のデータでは右肩上がり)を組み込む
3.1周期前(今回は12時点前)を予測値とする
1.は平均に回帰しない、非定常な時系列データに対して用いられるナイーブ予測です。
2.は、さらに右肩上がりのトレンドを組みこみました。
3.は、周期性を持つデータに対してしばしば用いられる方法で、前年同期の値を予測値としてそのまま使っているわけです。
こういった単純な予測に負けてしまうようでは情けないですね。こいつらに勝てるかどうかを評価しようということです。
ナイーブ予測はforecastパッケージを使うと簡単に計算できます。
## 特別な技術を要しない単純な予測手法 # 訓練データの最終時点を予測値とする f_rwf <- rwf(train, h = h) # 全体のトレンドを組み込む f_rwf_drift <- rwf(train, drift = TRUE, h = h) # 1周期前(今回は12時点前)を予測値とする f_snaive <- snaive(train, h = h)
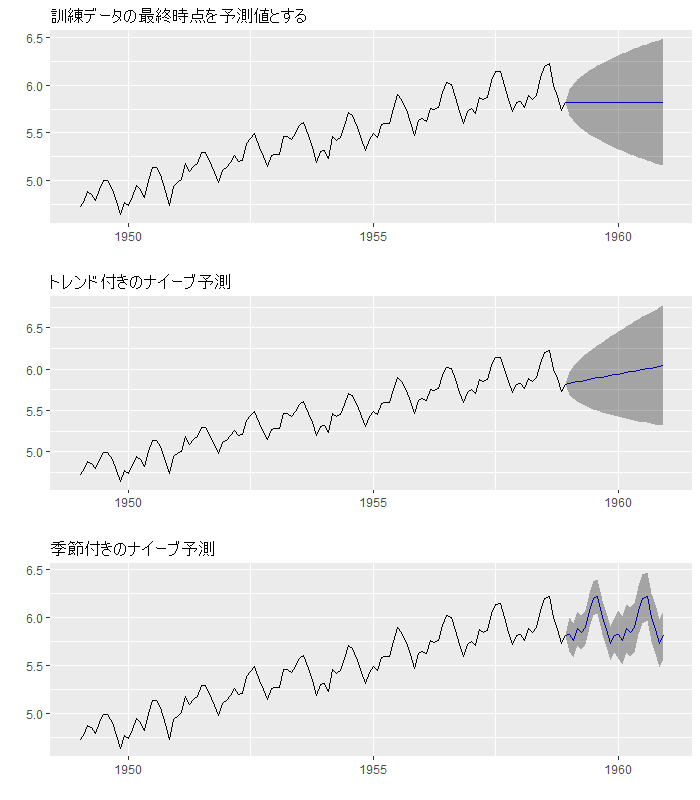
ナイーブ予測の結果も図示してみます。
autoplotの結果を各々p1~p3に格納して、3つまとめて表示します。
# 参考:ナイーブ予測の結果の図示 p1 <- autoplot(f_rwf, main = "訓練データの最終時点を予測値とする") p2 <- autoplot(f_rwf_drift, main = "トレンド付きのナイーブ予測") p3 <- autoplot(f_snaive, main = "季節付きのナイーブ予測") grid.arrange(p1, p2, p3, nrow=3)
このグラフを見ると、3つ目の季節付きのナイーブ予測はうまく予測ができているように見えます。
単なる前年同期を使っただけなのですが、このような単純な予測でも十分であることはしばしばあります。
こいつに勝てるかどうかが1つのポイントですね。
全部のRMSEを比較します。
> # 各々の予測結果のRMSEを比較する > accuracy(f_sarima, test)[, "RMSE"] Training set Test set 0.03539809 0.09593236 > accuracy(f_rwf, test)[, "RMSE"] Training set Test set 0.1058089 0.3230635 > accuracy(f_rwf_drift, test)[, "RMSE"] Training set Test set 0.1054032 0.2204105 > accuracy(f_snaive, test)[, "RMSE"] Training set Test set 0.1381999 0.1821230
訓練データでもテストデータで見ても、共にSARIMAモデルのRMSEが最小となっていることがわかりました。
まずは、うまく予測できてよかったね、というところでしょうか。
最後におまけとして、予測誤差のグラフを描いてみます。
数値で直接見てもなかなかわかりにくいですが、棒グラフなどにすると視覚的に理解できます。
ggplot2というパッケージを使うことで美麗なグラフを描くことができます。
そのためには、まずはデータフレームの形式になるように結果を整形する必要があります。
訓練データとテストデータのRMSEを並べて比較したいので、まずは凡例を用意しておきましょう。
> ## 図示するために、整形をする
> # 評価セットの凡例
> types <- c("train", "test")
> types
[1] "train" "test"
ここからの方針ですが、RMSEの計算結果を以下のように整形すると、ggplot2を使ってきれいなグラフを描くことができます。
> # 手作業でデータを整形する。
> # このコードをあと3回繰り返す……?
> acc_df_sarima <- data.frame(forecast = rep("f_sarima", 2),
+ type = types,
+ RMSE = accuracy(f_sarima, test)[, "RMSE"],
+ row.names = NULL)
> acc_df_sarima
forecast type RMSE
1 f_sarima train 0.03539809
2 f_sarima test 0.09593236
このコードをあと3回繰り返して頑張って整形しても良いのですが、面倒なので、簡単に整形できる便利関数を作ってみました。
この記事の中でしか使いませんので、少々適当に作ってありますが、最低限の動作はしてくれます。
# データを簡単に整形できる便利関数を自作する
make_acc_df <- function(forecast_name, types, rmse_vec){
# グラフにしやすい形式に、予測誤差を整形する関数
#
# Args:
# forecast_name: 予測の方法の名称
# types: 予測誤差のタイプ
# rmse_vec: RMSEが格納されたベクトル
#
# Returns:
# 整形された予測誤差のデータフレーム
vec_length <- length(rmse_vec)
acc_df <- data.frame(forecast = rep(forecast_name, vec_length),
type = types,
RMSE = rmse_vec,
row.names = NULL)
return(acc_df)
}
この関数は、名称と予測誤差のタイプ(今回は訓練データorテストデータ)とRMSEを渡すことで、整形されたデータフレームを出力してくれます。
動作を確認してみます。
> # 動作確認
> make_acc_df("f_sarima", types, accuracy(f_sarima, test)[, "RMSE"])
forecast type RMSE
1 f_sarima train 0.03539809
2 f_sarima test 0.09593236
うまくできていそうなので、これを使って4種類の予測のRMSEを一気に整形して、rbind関数を使って4種類の予測の結果を結合させます。
# 4つのRMSEを結合
acc_df <- rbind(
make_acc_df("f_sarima", types, accuracy(f_sarima, test)[, "RMSE"]),
make_acc_df("f_rwf", types, accuracy(f_rwf, test)[, "RMSE"]),
make_acc_df("f_rwf_drift", types, accuracy(f_rwf_drift, test)[, "RMSE"]),
make_acc_df("f_snaive", types, accuracy(f_snaive, test)[, "RMSE"])
)
こんな結果になります。
きれいになりましたね。こういう形式を整然データと呼びます。整然データに関しては『整然データとは何か|Colorless Green Ideas』等も参照してください。
> # 整形されたデータ。
> # 整然データの形式になっているので、扱いやすい
> acc_df
forecast type RMSE
1 f_sarima train 0.03539809
2 f_sarima test 0.09593236
3 f_rwf train 0.10580887
4 f_rwf test 0.32306346
5 f_rwf_drift train 0.10540316
6 f_rwf_drift test 0.22041052
7 f_snaive train 0.13819987
8 f_snaive test 0.18212295
後はこの結果を使ってグラフを描きます。ggplot2関数を使います。
# 図示
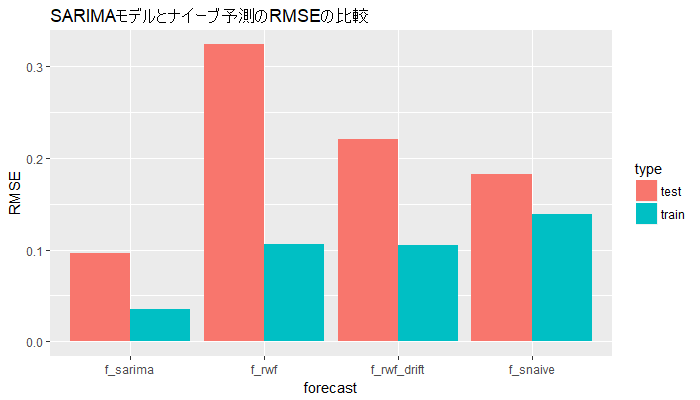
ggplot(acc_df, aes(x = forecast, y = RMSE, fill = type)) +
geom_bar(stat = "identity", position = "dodge") +
ggtitle("SARIMAモデルとナイーブ予測のRMSEの比較")
これなら結果が一目ですね。
SARIMAモデルのRMSEが最も小さいようです。
今回は標準的なやり方でデータを整形しましたが、dplyer等を使うともう少し短いコードで済むかもしれません。
もっといいやり方があれば、ご指摘いただけますと幸いです。
5.クロスバリデーション法による予測の評価
先ほどはデータを2分割して予測誤差を評価しました。
しかし、これにはいくつか不満な点があります。
1.予測を1回しか行っていない→複数回の予測を行い、予測誤差を正確に評価したい
2.何時点先の予測が当たりやすいor当たりにくいかがわからない→1時点先の予測誤差、2時点先の予測誤差と別々に求めたい
2番は地味に重要でして、例えば「2時点先(今回のデータでは2か月先)までは精度よく予測できるが、3時点先になると予測誤差が大きくなる」みたいなことがわかれば、予測の運用において大きな情報となります。予測を用いた意思決定をしたいならば、なるべく2時点先までの結果だけを使ってね、と運用側に注意を呼び掛けるわけです。
こういうのを簡単にやっつけてしまおうということで使うのが、forecastパッケージのtsCV関数です。
tsCV関数での予測の評価には大きく2つのやり方があります。
1つ目は訓練データの「開始時点」を1時点目に固定して、そこから1つずつ訓練データを増やしていくというものです。
■を訓練データ
□をテストデータ
とします。
また、2時点先までを予測して、その評価を行うとしましょう。
以下のように訓練データ、テストデータが用いられます。
1回ごとに、訓練データが増えていくことに注意してください。
データが少ない場合などにしばしば使われます。
■□□
■■□□
■■■□□
■■■■□□
■■■■■□□
実装してみましょう。
tsCV関数の引数には、予測結果を出力する関数を入れます。
そこで、訓練データを入れると、SARIMAモデルを推定して、予測結果を出力してくれる関数を自作するところから始めましょう。
まずは、最適な次数がいくつだったかを確認しておきます。
> # 次数の確認
> mod_sarima
Series: train
ARIMA(0,1,1)(0,1,1)[12]
Coefficients:
ma1 sma1
-0.3424 -0.5405
s.e. 0.1009 0.0877
sigma^2 estimated as 0.001432: log likelihood=197.51
AIC=-389.02 AICc=-388.78 BIC=-381
ARIMA(0,1,1)(0,1,1)でしたね。
この次数を使って、予測結果を出力してくれる関数を自作します。
# データを入れると、すぐに予測結果が出力される関数を作る
f_sarimax_func <- function(ts_data, h){
# 訓練データと予測期間を指定すると、予測結果が出力される関数
#
# Args:
# ts_data:訓練データ
# h:予測期間
#
# Returns:
# forecast関数による予測の結果
# 選ばれたモデルと同じ次数のARIMAモデルを推定
mod <- Arima(ts_data, order = c(0,1,1), seasonal = c(0,1,1))
# 予測結果を出力
return(forecast(mod, h = h))
}
動作確認をします。
> # 動作確認
> kakunin <- f_sarimax_func(train, h = h)
>
> head(kakunin$mean)
Jan Feb Mar Apr May Jun
1959 5.853880 5.803858 5.948464 5.920534 5.947908 6.116194
> head(f_sarima$mean)
Jan Feb Mar Apr May Jun
1959 5.853880 5.803858 5.948464 5.920534 5.947908 6.116194
うまくできているようなので、あとはこれをtsCV関数の引数に入れるだけです。
SARIMAモデルだけではなく、ナイーブな予測の予測の評価もあわせて行いました。
データが小さいので、数秒で終わります。
# クロスバリデーション法の実行 # h=3で実行 h <- 3 sarima_cv <- tsCV(log_air_pass, f_sarimax_func, h = h) rwf_cv <- tsCV(log_air_pass, rwf, h = h) rwf_drift_cv <- tsCV(log_air_pass, rwf, h = h, drift = TRUE) snaive_cv <- tsCV(log_air_pass, snaive, h = h)
結果を確認してみます。SARIMAモデルの評価結果を出力します。
> # 結果の確認
> sarima_cv
h=1 h=2 h=3
Jan 1949 NA NA NA
Feb 1949 NA NA NA
Mar 1949 NA NA NA
Apr 1949 NA NA NA
May 1949 NA NA NA
Jun 1949 NA NA NA
Jul 1949 NA NA NA
Aug 1949 NA NA NA
Sep 1949 NA NA NA
Oct 1949 NA NA NA
Nov 1949 NA NA NA
Dec 1949 NA NA NA
Jan 1950 NA NA NA
Feb 1950 NA NA NA
Mar 1950 -2.049961e-02 -0.0334477724 0.0326897899
Apr 1950 -7.194391e-03 0.0589540035 0.0988687074
May 1950 7.191144e-02 0.1118407031 0.1118574929
Jun 1950 8.280028e-02 0.0828002756 0.0941542596
Jul 1950 -3.139856e-03 0.0081735779 -0.0305860615
Aug 1950 1.255202e-02 -0.0262045463 -0.0456688468
Sep 1950 -4.528734e-02 -0.0648050747 0.0142346657
Oct 1950 1.211607e-03 0.0803617959 0.1412139429
Nov 1950 7.860547e-02 0.1394559241 0.0820226564
Dec 1950 1.971271e-02 -0.0213144066 0.0374963931
Jan 1951 -6.415114e-02 -0.0055931463 -0.0440372741
・・・中略・・・
Sep 1960 2.963461e-02 -0.0094006940 -0.0134263799
Oct 1960 -2.720049e-02 -0.0312582943 NA
Nov 1960 -1.500723e-02 NA NA
Dec 1960 NA NA NA
注目すべきはNAが大量にある点です(中略で消したところにNAはありません)。
SARIMAモデルは季節性を組み込んだモデルですので、最低でも1年以上の訓練データがなければモデルを構築することができません。そのため、最初の1年と少しはすべてNAです。
また、3時点先までを予測しようとしているので、3時点先の回答データがない末尾においてもやはりNAが出力されます。
出力の説明をしておきます。
『Mar 1950』の行は「Mar 1950までのすべてのデータを使ってモデルを構築した結果」が出力されています。
『h=1』列目は1時点先の予測残差(実測値-予測値)が出力されます。
『Mar 1950』行の『h=1』列目は、1950年4月の予測残差となり、
『Mar 1950』行の『h=2』列目は、1950年5月の予測残差となります。
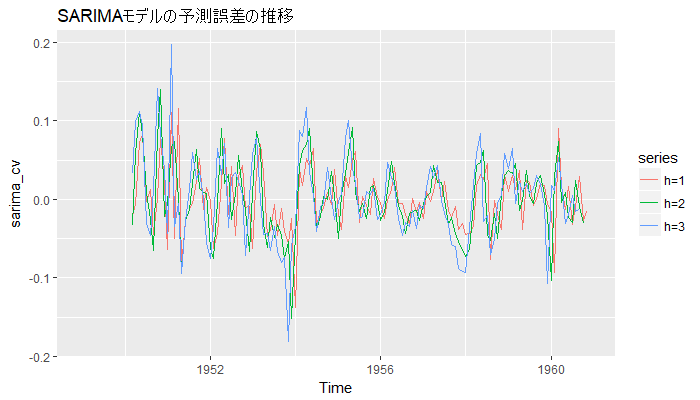
次に移る前に、訓練データの大きさと予測誤差の対応を図示して確認してみます。
1955年以降は、安定してそうに見えます。
# 予測誤差の図示(訓練データにおける時点も含む) # どれくらいのデータがあれば、予測結果が落ち着くのかを判断する目安にもなる autoplot(sarima_cv, main = "SARIMAモデルの予測誤差の推移")
次に行きましょう。
やることは、ナイーブな予測とのRMSEの比較です。
NAが大量にあるので、まずはこれを削除します。na.omit関数を使います。
また、テスト期間は1959年以降ですので、この結果だけを使うことにします。
# 予測の評価からは訓練データが含まれる時点を除いたうえで、 # NULLの無い年を使う sarima_cv_test <- na.omit(window(sarima_cv, start = c(1959, 1))) rwf_cv_test <- na.omit(window(rwf_cv, start = c(1959, 1))) rwf_drift_cv_test <- na.omit(window(rwf_drift_cv, start = c(1959, 1))) snaive_cv_test <- na.omit(window(snaive_cv, start = c(1959, 1)))
データの抽出が終わったので、あとはRMSEを計算するだけなんですが、残差からRMSEを計算する関数がforecastパッケージには用意されていないようだったので、自作します。
コメントが長いんですが、実質1行で終わる簡単な関数です。
# RMSEを計算する関数を作る
calc_rmse <- function(target_resid){
# 予測残差を入れるとRMSEが出力される関数
#
# Args:
# target_resid:予測残差(y - y_hat)
#
# Returns:
# RMSE
return(sqrt(mean(target_resid^2)))
}
この関数を使って、SARIMAモデルにおけるRMSEを計算します。
apply関数の2つ目の引数に「2」を、3つ目の引数にcalc_rmseを入れると、列を対象にしてcalc_rmseを一気に実行した結果を出力してくれます。
> # 予測期間別のRMSE
> apply(sarima_cv_test, 2, calc_rmse)
h=1 h=2 h=3
0.03497509 0.03579213 0.03478006
前回と同様に、整形した後に、ggplot2を用いて図示します。
## データを整形し、棒グラフを描く
# 凡例
types <- c("h=1", "h=2", "h=3")
# 整形されたデータ
acc_df_cv <- rbind(
make_acc_df("f_sarima", types, apply(sarima_cv_test, 2, calc_rmse)),
make_acc_df("rwf", types, apply(rwf_cv_test, 2, calc_rmse)),
make_acc_df("rwf_drift", types, apply(rwf_drift_cv_test, 2, calc_rmse)),
make_acc_df("snaive", types, apply(snaive_cv_test, 2, calc_rmse))
)
# 図示
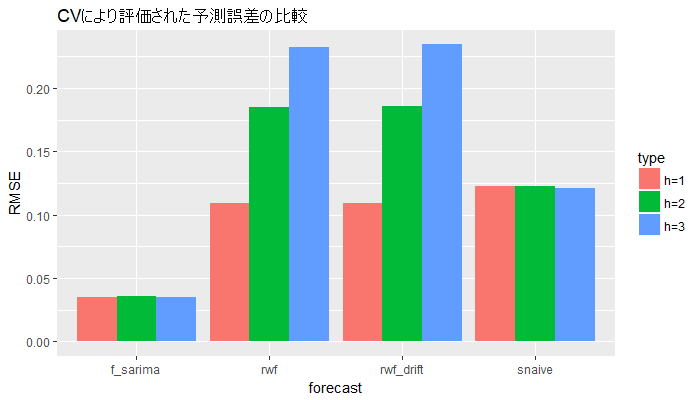
ggplot(acc_df_cv, aes(x = forecast, y = RMSE, fill = type)) +
geom_bar(stat = "identity", position = "dodge") +
ggtitle("CVにより評価された予測誤差の比較")
やはりSARIMAモデルのRMSEが最も小さいようです。
続いて、何時点先までの予測であれば、精度よく予測できるのか、確かめてみましょう。
予測期間をh=12として長くしたうえで、tsCV関数を実行します。
> # 予測誤差はどの時点まで変わらない?
> sarima_cv_24 <- tsCV(log_air_pass, f_sarimax_func, h = 12)
> sarima_cv_24 <- na.omit(window(sarima_cv_24, start = c(1959, 1)))
> sarima_cv_24
h=1 h=2 h=3 h=4 h=5
Jan 1959 9.695296e-03 0.036555287 0.039490352 0.071091263 0.019721211
Feb 1959 3.006934e-02 0.032940977 0.064700521 0.013556406 0.050204492
Mar 1959 1.302989e-02 0.045093082 -0.005616613 0.031095698 0.043646779
Apr 1959 3.657371e-02 -0.013968936 0.022767888 0.035431202 0.019516340
May 1959 -3.859335e-02 -0.001898504 0.010571798 -0.004811287 -0.002001832
Jun 1959 2.383532e-02 0.036765299 0.020102095 0.022991303 0.042730875
Jul 1959 2.107665e-02 0.004842354 0.007706171 0.027505575 0.037876836
Aug 1959 -8.453780e-03 -0.005620908 0.014247916 0.024864722 0.013107243
Sep 1959 -4.299025e-05 0.019875629 0.030667158 0.018785031 0.004594273
Oct 1959 1.989131e-02 0.030655633 0.018792949 0.004585004 -0.083035399
Nov 1959 1.759474e-02 0.005831238 -0.008465394 -0.096048096 0.025943442
Dec 1959 -5.560612e-03 -0.020055492 -0.107556772 0.014404668 -0.002672862
h=6 h=7 h=8 h=9 h=10
Jan 1959 0.056335573 0.0684252585 0.054068670 0.056805356 0.076870581
Feb 1959 0.062455295 0.0476676145 0.050435838 0.070439470 0.081526616
Mar 1959 0.028042105 0.0308662271 0.050754055 0.061437683 0.049632708
Apr 1959 0.022360381 0.0422045568 0.052734444 0.041038899 0.026680690
May 1959 0.017917284 0.0287105591 0.016827504 0.002637848 -0.084990434
Jun 1959 0.052888667 0.0414558505 0.026851054 -0.060606650 0.061339070
Jul 1959 0.026293443 0.0118313334 -0.075683148 0.046283111 0.029154974
Aug 1959 -0.001194799 -0.0887752281 0.033215459 0.015836775 -0.003794462
Sep 1959 -0.083033533 0.0389750336 0.021418732 0.001847635 0.023536986
Oct 1959 0.038970357 0.0214416788 0.001861036 0.023571438 -0.015441825
Nov 1959 0.008556191 -0.0110722121 0.010745640 -0.028178377 -0.024906352
Dec 1959 -0.022399438 -0.0003481843 -0.039078108 -0.036238004 -0.002793962
h=11 h=12
Jan 1959 0.088169803 0.07592215
Feb 1959 0.069432339 0.05542497
Mar 1959 0.035373482 -0.05222502
Apr 1959 -0.060876313 0.06110563
May 1959 0.037018313 0.01946024
Jun 1959 0.044429652 0.02465342
Jul 1959 0.009443843 0.03145714
Aug 1959 0.018029882 -0.02088874
Sep 1959 -0.015493751 -0.01198702
Oct 1959 -0.011973389 0.02141582
Nov 1959 0.008500399 -0.03052077
Dec 1959 -0.041751766 -0.04591227
1年先までを予測対象としているので、最終年は評価結果に表れないことに注意してください。
予測期間を変えると、評価対象となるデータまで変わってしまうのが難しいところです。
前回同様、データを整形したうえで図示します。
凡例が12パターンもあって作るのが大変なので、ちょっと工夫して作ります。
formatC関数で『width=2, flag=”0″』と指定すると、頭を0埋めにしてくれます。グラフの並び順をきれいにする(h=1の隣にh=10が来ないようにする)ために指定しました。
> ## データを整形し、棒グラフを描く
>
> # 凡例
> types <- paste("h=", formatC(1:12, width=2, flag="0"), sep="")
> types
[1] "h=01" "h=02" "h=03" "h=04" "h=05" "h=06" "h=07" "h=08" "h=09" "h=10" "h=11"
[12] "h=12"
後はほぼ同じ方針で図示できます。
SARIMAモデルしか対象になっていないので、『fill = type』と指定するのを無くし、色分けをやめました。
# 整形されたデータ
acc_df_cv_24 <- make_acc_df("sarima_cv_24", types, apply(sarima_cv_24, 2, calc_rmse))
# 図示
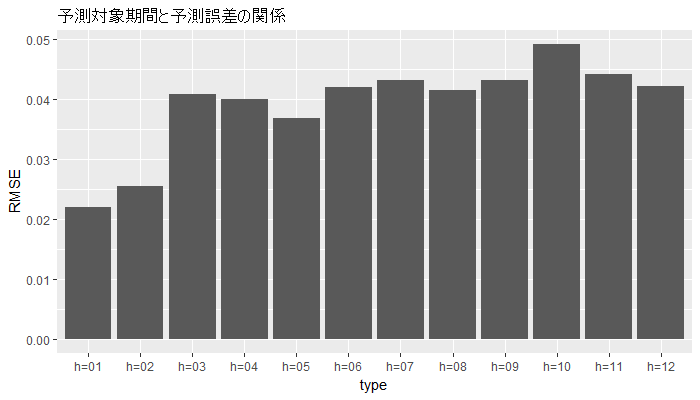
ggplot(acc_df_cv_24, aes(x = type, y = RMSE)) +
geom_bar(stat = "identity", position = "dodge") +
ggtitle("予測対象期間と予測誤差の関係")
グラフで見ると、2時点先までは精度が良くて、3時点先からはちょっとRMSEが大きくなりそうだなということがわかります。
6.スライド型のクロスバリデーション法の実行
最後に、スライド型のクロスバリデーション法を実行します。
訓練データの大きさをwindowで指定し、これをスライドさせることで、一定の大きさの訓練データを常に使います。
簡単な概略図を示します。
■:訓練データ
□:テストデータ
×:使わないデータ
window=3, h=2の時
■■■□□
×■■■□□
××■■■□□
tsCV関数に『window』という引数を入れることを除けば、ほとんど同じコードで実装できます。
予測残差を求めたうえで、NAを排除するところまでまとめてやってしまいます。
# h=3, window=訓練データのサンプルサイズで実行 window_cv <- length(train) h <- 3 # 予測誤差の計算 sarima_window <- tsCV(log_air_pass, f_sarimax_func, h = h, window = window_cv) sarima_window <- na.omit(window(sarima_window, start = c(1959, 1)))
RMSEを求めます。
> # RMSEを求める
> apply(sarima_window, 2, calc_rmse)
h=1 h=2 h=3
0.03509483 0.03597696 0.03487521
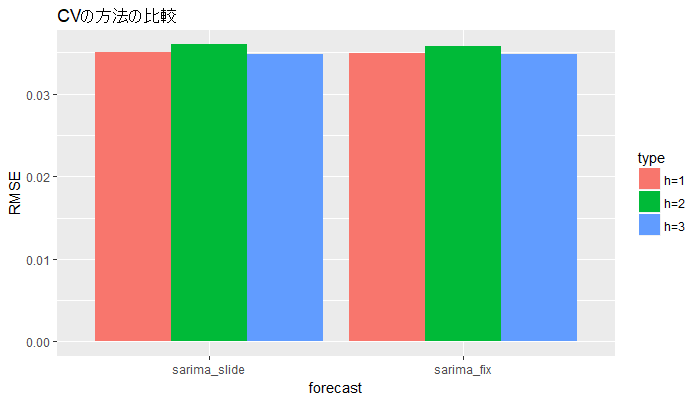
せっかくですので、2つのクロスバリデーション法の比較をしてみます。
## CVの方法の違いの比較
# 凡例
types <- c("h=1", "h=2", "h=3")
# データの整形
acc_df_cv_pattern <- rbind(
make_acc_df("sarima_slide", types, apply(sarima_window, 2, calc_rmse)),
make_acc_df("sarima_fix", types, apply(sarima_cv_test, 2, calc_rmse))
)
# 図示
ggplot(acc_df_cv_pattern, aes(x = forecast, y = RMSE, fill = type)) +
geom_bar(stat = "identity", position = "dodge") +
ggtitle("CVの方法の比較")
グラフを見ると、大して変化はなさそうです。
7.後記
後記というよりかは、補足であったりいいわけであったりをここに記します。
tsCV関数に関しては、forecastパッケージの作成者の以下の記事も参照してください。
Cross-validation for time series
時系列データへのクロスバリデーション法を説明したわけですが、時系列データだからといって常にこの方法でなければならないというわけではありません。単純な自己回帰モデルで表現可能な場合は、通常のk-fold-CVを使っても支障ないようです。
A note on the validity of cross-validation for evaluating autoregressive time series predictionという論文も参照してください。
今回はtsCV関数を使ったわけですが、こういった関数を自作することも難しくはありません。tsCV関数は指定できる箇所がやや少ないです(例えば固定型のCVにおいて、データを2個ずつ増やしたい、と思っても、この関数では実行できない)。この記事の最後に参考文献としてあげた「前処理大全」などにtsCVを使わない方法が載っています。
後は、書いていて思ったことを雑に記します。
今回はやや長いコードとなりました。長いコードをRで書く場合はセクションを区切ると便利です。RStudioを使っている場合は「Ctrl+Shift+R」でセクションを挿入することができます。
関数の作成をする箇所も3カ所ありましたね。本来は関数を書くのは単一のセクションにまとめてしまうと見通しが良くなります。私の場合は実際の処理を行う前に「utility関数」みたいなセクションを作ってその中に突っ込むことがしばしばあります。今回は説明のためにあっちこっちで関数を定義しましたが、できるだけまとめましょう。別のファイルに関数を定義してsource関数を使って読み込むこともあります。
関数には、なるべくコメントを残しておいた方が、後で読みやすいです。calc_rmseみたいに、書くのが馬鹿らしくなるような短い関数もあります。しかし、引数が残差だったのか予測値と実測値両方入れるんだったか、忘れちゃった、みたいな問題は、コメントを書くことで防ぐことができます。この記事のコメントの書き方が最善であるとは考えにくいので、色々なサイトの書き方を参照してみてください。
命名規則はやや適当なので、もう少し考えてコードを書いた方が良かったですね。
ggplot2はbiopapyrusさんの記事を参考にさせていただきました『geom_bar|ggplot で棒グラフを描く方法』。
0埋めに関しては、『数値の頭に0を詰めて桁を揃える|My Life as a Mock Quant』を参照させてもらいました。
最後に、一瞬だけ出てきた整然データですが、この用語は小学校の「情報」の教科書に出てきてもいいくらいのものだと思います。宣伝のために、もう一度リンクを載せておきます『整然データとは何か|Colorless Green Ideas』。
論文も出ているようです。引用しやすくなったので助かります。
『整然データとは何か』
参考文献
|
時系列分析と状態空間モデルの基礎:RとStanで学ぶ理論と実装 管理人が書いた時系列分析の入門書です。SARIMAモデルの仕組みを知りたいという方や、他の時系列モデルについて学びたいという方は、こちらも読んでいただけると幸いです。 サポートページはこちらです。 重版に合わせて、出版社サイトにて第1部の1~2章が立ち読みできるようになりました。 |
 |
|
前処理大全 通称Awesome本と呼ばれる書籍です。Awesomeとは「素晴らしい」とか「驚くばかり」という意味らしいですね。 タイトルの通り、データの効率的な前処理の方法が記されていて、便利です。 |
 |
スポンサードリンク
更新履歴
2018年4月24日:新規作成
2018年4月25日:GitHubへのリンクを追加