時系列分析のためのブックガイド

新規作成：2018年03月05日
最終更新：2018年03月06日

この記事は、時系列分析をこれから学ぼうとされる方のためのブックガイドです。
書籍によってカバーされている範囲、R言語などのプログラミング言語を援用しているかしていないか、そして書籍の難易度などをまとめています。
また、私自身、「時系列分析と状態空間モデルの基礎」という時系列分析の入門書を執筆しており、この本がどのような立ち位置にあるのかも説明しています。

目次

1. 書籍紹介
2. 時系列分析のトピック
3. 状態空間モデルの分類
4. 古典的な時系列モデルを学ぶことの意義
5. 書籍で扱われている内容の比較
6. 隼時系列本の立ち位置

 

1．書籍紹介

Rによる実装なし

沖本(2010)『計量時系列分析』   以下「沖本本」と略します。 実用的でバランスも良く、当サイトでも強く推している書籍です。 ARIMA・GARCH・見せかけの回帰などが丁寧に説明されています。 状態空間モデルについてはあまり載っていません。 難易度はやや高めです。

北川(2005)『時系列解析入門』   以下「北川本」と略します。 時系列分析の第一線で活躍された先生が書かれた、これも著名な書籍です。 ARMA・状態空間モデルの解説があり、粒子フィルタの解説も載っています。 GARCHや見せかけの回帰といった話題はあまり載っていません。 難易度はやや高めです。

Rによる実装あり

田中(2008)『Rによる時系列分析入門』   以下「田中R本」と略します(田中 勝人先生の別の本と区別するため)。 数理的な側面も丁寧に記載されています。 時系列モデル以前の指数平滑化といった基礎からSARIMAモデルの推定まで扱います。 状態空間モデルの記載はありません。 難易度は中くらいです。

横内・青木(2014)『現場ですぐ使える時系列データ分析』   表紙が青いので、以下「時系列青本」と略します。 金融実務に詳しい方が書かれているようで、実践的な内容が多いです。 自己回帰モデルからGARCHモデルまでを扱います。 状態空間モデルの記載はありません。金融の話題が多めです。 難易度は低いので、初学者にもお勧めします。

野村(2016)『カルマンフィルタ』   以下「野村本」と略します。 Rで学べる状態空間モデルの入門書です。理論と実装のバランスが素晴らしいです。 ARMAの概要からカルマンフィルタ・粒子フィルタまでコンパクトにまとめてあります。 GARCH・見せかけの回帰の記載はありません。 難易度は中くらいでしょうか。高度な内容ですが、Rを併用するのでとっつきやすいです。初学者の方はこの本を理解することを目標にするのが良いかと思います。

岩波データサイエンス vol.6   以下「岩波DS6」と略します。 この分野の第一人者である豪華執筆陣による、新しいタイプの時系列分析の書籍です。 「状態空間モデルから始まる時系列分析」に注力し、Rによる粒子フィルタの実装コードも含まれます。 逆に、古典的なモデルの解説はVARがあるのみです。 様々なトピックを解説した書籍ですので、難易度は一概には答えられません。「状態空間モデル」という最初の記事は、時系列分析のエッセンスがつまっていますが、少し難しいかもしれません。しかし、ほかの書籍を読んだあとに読み返すと、とてもきれいに整備されていることに気が付くはずです。

MCMCと状態空間モデル

岩波データサイエンス vol.1   以下「岩波DS1」と略します。 時系列分析の本ではなくMCMCといったベイズ推論に関する書籍です。 MCMCを用いた状態空間モデルの推定の方法とRコードなどが載っています。 様々なトピックを解説した書籍ですので、難易度は一概には答えられません。「ベイズ超速習コース」という最初の記事は、難易度が低いうえに重要なエッセンスが含まれています。

松浦(2016)『StanとRでベイズ統計モデリング』   以下「アヒル本」と略します。 時系列分析の本ではなくベイズ統計モデリングの入門書です。 MCMCを用いた状態空間モデルの推定の方法とRコードなどが載っています。 Stanの使い方に関しては、最も詳細な本です。 とても丁寧に書かれているので、難易度は低めです。

自著

馬場(2018)『時系列分析と状態空間モデルの基礎』   表紙がハヤブサなので、以下「隼時系列本」と略します。 「沖本本＋状態空間モデル」の内容を、初学者向けにRやStanコードも併用して解説した本です。 非ガウシアンなモデルに対してはMCMCによる状態空間モデルの推定方法を載せています。 粒子フィルタについての解説はありません。 難易度は低めです。

 

2．時系列分析のトピック

上記の一言解説で自分の必要としている本がわかった人は、以下を読む必要はありません。
ここからは「そもそも時系列分析で学ぶテーマは何だろう」という「時系列分析を学ぶ前」の話をします。

時系列分析は主に以下の4つに大別されると考えます。ただし、カオス時系列分析はここに分類されません。
イメージとしては1が最も古く、順に新しくなっていきます。ただし3と4はどちらが最新かという区別は付けられません。

1．統計モデル以前の枠組み：指数平滑化やHolt-Winters法
2．ARIMAモデルとその周辺：Box-Jenkins法、VAR、GARCHを含む
3．状態空間モデル
4．曲線フィッティング：prophetや機械学習法

各々を簡単に紹介します。

1．統計モデル以前の枠組み：指数平滑化やHolt-Winters法

時系列データをどのように分析するべきか、という工夫は過去から続いてきたものです。
統計モデルが用いられる前の古典的な分析手法は「時系列データの特徴の一部のみに焦点を当てた計算手法」と考えると良いでしょう。

例えば、時系列データは「過去と未来が似ている」という関係があることが多いです。例えば、昨日の売り上げが高ければ、今日も良く売れるだろう、といった関係です。
この「時系列データの前後関係を表現するという”だけ”」で予測式を構築するものとして、例えば指数平滑化法という時系列の予測手法があります。

ほかにも「時系列データは、トレンド＋周期性＋ホワイトノイズに分割できるはずだ」と考え、この関係性のみを用いた予測式を提案することも試みられました。それがHolt-Winters法です。

時系列データの特徴を捉えることには成功しているものの、例えば「前後関係＋季節性＋トレンド＋外因性、全部必要だ！」といった場合に、「時系列データの特徴の一部のみに焦点を当てた計算手法」では力不足でした。

2．ARIMAモデルとその周辺：Box-Jenkins法、VAR、GARCHを含む

次に出てきたのが統計モデルの活用です。
統計モデルを用いることで、様々な拡張が可能となりました。

最も基本的な時系列モデルであるARMAモデルは、単純な構造でありながら線形定常過程においては極めて高い予測精度を誇ります。
ARMAモデルの拡張である「前後関係＋季節性＋トレンド＋外因性」をすべて含んだSARIMAXモデル、そしてモデルを推定するための具体的な手順を取りまとめたBox-Jenkins法は、時系列分析の一つの集大成といえるでしょう。

また、背後に確率分布・データ生成過程という概念を持つので、得られたデータについての解釈や「予測の外れ具合」への言及など様々な活用ができるようになった点も見逃せません。

ARモデルを多変量に拡張したVARモデルは「複数の時系列データ間での相互関係」を探る強力なツールとして現在でも用いられています。

さらにファイナンスデータの解析から生まれたGARCHモデルは「分散の変動をモデル化する」という斬新なアイデアを提供し、考案者はノーベル経済学を受賞しました。

3．状態空間モデル

統計モデルの使用を前提とした時系列分析は、より自由に、より人間の直感を取り込めるような形へと進化していきます。それが状態空間モデルです。
状態空間モデルは目に見えない「状態」を用いることで、時系列データをより柔軟にモデル化することを可能にしました。私たち人間にとっての解釈という点で見ても、モデルの拡張のしやすさという点で見ても大きな進歩といえます。
状態空間モデルはARIMAモデルといった古典的な統計モデルを包含したモデルであることにも注意が必要です。純粋な「拡張」とみなすことができるわけです。

書きたいことは山ほどあるんですが、スペースが足りません。「状態空間モデル」や「なぜ状態空間モデルを使うのか」といった記事も参照してください。

4．曲線フィッティング：prophetや機械学習法

指数平滑化やHolt-Winters法。これらは「過去の遺物」ではありません。単純なモデルは決して死ぬことが無いのです。優れたアイデアは形を変えて残り続けます。
私たちは複雑な計算でも短時間で完了できる素晴らしいコンピュータ資源を、そして優れた最適化のためのアルゴリズムを手に入れました。時系列データの特徴1つ1つをいわば無理やりHolt-Winters法にすべて突っ込むということもやろうと思えばできるはずです。
実際にそれをやったライブラリがあります。prophetです。prophetはHolt-Winters法の大規模な拡張だと思うと良いです。

より複雑な構造、例えばニューラルネットワークといったものも時系列分析に活用することは少しずつ進んでいくはずです。ただし、現状はBox-Jenkins法のようなベストプラクティスや状態空間モデルのような体系立てられた手法はなかなかない印象です。シンプルな線形モデルの方が予測精度が高いことはしばしばあり、機械学習を自在に時系列データに適用するには、もう少しノウハウの蓄積が必要かもしれません。
これらも見逃せない潮流ですが、書籍がほとんど無いのが現状です。

 

3．状態空間モデルの分類

prophetを除けば現代時系列分析の中心にあるといえるのが状態空間モデルです。
ただし、状態空間モデルといってもあまりにも幅が広いので、さらにいくつかに分類します。
詳しくは『状態空間モデルの推定方法の分類』も参照してください。

まずは適用できる対象です。
線形ガウス状態空間モデルはその名の通り「線形ガウス」なデータにしか適用できません。これは動的線形モデルとも呼ばれます。
線形非ガウス状態空間モデルは動的一般化線形モデルとも呼ばれます。
非線形非ガウス状態空間モデルは一般化状態空間モデルとも呼ばれます。文献によってはこちらが単なる「状態空間モデル」とされることもあります。

次は推定の方法です。
線形ガウス状態空間モデルは「カルマンフィルタ＋最尤法」の組み合わせが使われるのが普通です。単にカルマンフィルタと呼ぶことにします。
一方で非ガウスのモデルになると、推定方法がいくつかに分かれます。

非線形非ガウス状態空間モデル(一般化状態空間モデル)では、「粒子フィルタ」または「MCMC法」を使うことができます。
粒子フィルタは逐次的な処理であり、MCMC法はバッチ型(まとめて計算)の処理となります。

 

4．古典的な時系列モデルを学ぶことの意義

先ほど状態空間モデルはARIMAモデルといった古典的な統計モデルを包含したモデルであると説明しました。
それでは状態空間モデル以前の古典的な時系列モデルを学ぶ必要はないのでしょうか。

これは単純に、自分に合った勉強方法を選んでいただければと思います。
最終的には状態空間モデルに行きつきます。そこへ至るルートが少し変わるだけです。

状態空間モデルの優れた教科書(野村本とか)が出てきていますので「最初から状態空間モデル」で学ぶことは十分現実的ですし、お勧めできるルートです。

ただ、私個人としては、古典的な時系列モデルも学んでほしいかなと思います。
あえて言えば、統計モデル以前の指数平滑化やHolt-Winters法でさえ学ぶことは十分な価値があると考えています。
というのも「状態空間モデルのパーツ」として先に古典的な時系列モデルを学ぶと、実際に分析に対してスムーズに取り組むことができるのではないかと思うからです。
古典的な時系列モデルを1つ学ぶということは「時系列データの1つの特徴とその表現方法を学ぶ」ということとほぼ等しいのですから。

状態空間モデルは「状態空間モデルというフレームワーク」ありきの設計です。このフレームワークの中において、構造を変化させてデータに適用します。
一方の古典的な手法は「データの特徴」ありきの設計です。この時系列データには時間の前後関係があって、それを表すのにARMAモデルを考案しました。分散の不均一性が認められるからGARCHモデルを構築しよう。こういった具合です。ですので「俺はARMAモデルがいいんだ！」というこだわりを持つと正しいモデリングはできません。様々な手法の使い分けが必要となります。

最終的にはすべて状態空間モデルの形式で記述されるべきです。だってその方がきれいだから。状態空間モデルは決して応用編ではなく、初学者でも状態空間モデルに触れ、これを中心に学ぶ必要があると思います。
でも時系列分析をこれから学ぶ方にとっては、先に「状態空間モデルのパーツ」から学ぶと、実践的な能力が身につくと思います。
何でもできる道具を渡されて、何をやればいいのか途方に暮れるのは、良い状況ではないはずです。

整理された情報を「整理がされている」と認識するためには、相応の知識が必要です。
整理された情報を使いこなすことも同様です。
そのための知識・技術を効率的に学ぶ方法として、古典的な時系列モデルを「ざっと流す」のは効率の良い勉強方法ではないかなと思います。

あと、古典的な時系列モデルを学ぶと、定常性や和分過程といった時系列分析の用語を(形式的にではなく)実際の分析を通して学ぶことができるのも大きなポイントです。この辺の用語はBox-Jenkins法を通して学ぶと、この概念の必要性なども併せて、きれいに整理できます。
※ もちろん、古典的なモデルで十分に対応できる状況もあります。古典的なモデルが実用的で無いという意味ではありません。

 

5．書籍で扱われている内容の比較

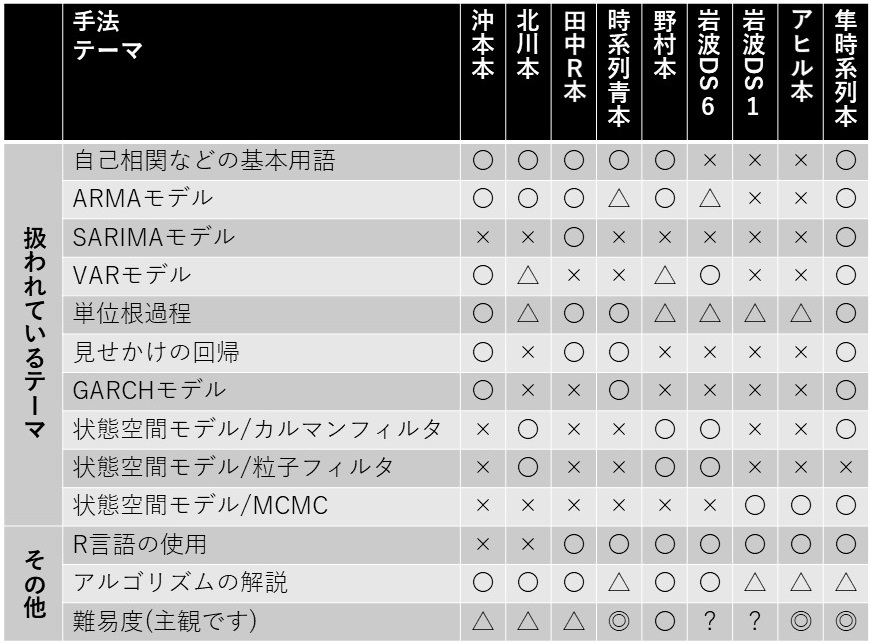
最後にまとめとして、先に紹介した時系列分析の入門書における、簡単な比較表を作ってみました。内容については統計モデルのみを対象としています。
これは私自身の主観も込められているので、参考までにお使いください。
誤りがあればご指摘ください。

拙著(隼時系列本)に丸印ばかりついていますが、これはずるをしたのであたりまえです。
この表に丸がつくように内容を決めて企画・執筆しましたので。
ほかの書籍よりも優れているわけではないことに注意してください。あと、この記事の内容もある程度はポジショントークが含まれます。

以下は、この表の補足です。○×は主に索引を見て付けました。岩波DSは索引がないので、ややアバウトです。
ARMAモデル：ARIMAかARMAどちらかに言及があれば〇にしています。時系列青本はほぼARモデルのみが対象なので△です。岩波DS6はARモデルのみ言及があるので△です。アヒル本は索引にARIMAがあるものの、書籍内での解説がないので×にしています。
SARIMAモデル：ARMAと分けたのは季節性の取り扱いが異なることがあるからです。沖本本は季節調整についてはほとんど言及していないですし、時系列青本のような金融時系列でも季節性の言及が少ないので、別途分けました。北川本・野村本・岩波DS・アヒル本では状態空間モデルで季節性を取り扱っています。
VARモデル：北川本・野村本に直接の記載はないんですが、多変量の時系列モデルの言及があるので△にしました。
単位根過程：単位根という言葉が索引に無くても、状態空間モデルで1次差分のモデルを構築している場合は△としています。単位根のあるデータに対する分析はすべての本で記載があるということです。
アルゴリズムの解説・難易度：これは完全に私の主観です。異論は認めます。

※この表は主に沖本本の目次から作ってあります。ただし、沖本本の最終章「状態変化を伴うモデル」は抜いています。TARモデルなどは沖本本以外に解説されている書籍が少ないためです。

6．隼時系列本の立ち位置

拙著「時系列分析と状態空間モデルの基礎」通称「隼時系列本」の立ち位置を説明します。

隼時系列本は、「沖本本＋状態空間モデル」をR言語で行うことを確定事項としていました。目次案からここはまったく変わっていません。
沖本本は、やや古典的な時系列分析の基礎を学ぶにおいて、極めてバランスよく用語・モデル・概念・数式の説明が配置された名著です。しかし、実装の仕方と状態空間モデルへの言及がないので、これを補おうという目的でした。
また、沖本本を補う目的で、季節性の取り扱いにも言及し、SARIMAXや基本構造時系列モデル(状態空間モデルでの季節性の取り扱い)を盛り込みました。
※沖本本の方が個別のテーマについてはより詳細に書かれています。例えば見せかけの回帰問題で共和分についての深い議論があるのは沖本本だけです。隼時系列本は沖本本のテーマの中で、より基本的な部分を取り上げたものだとご理解ください。隼時系列本を読んだ後に沖本本を読むと、多くの発見があるはずです。

また、徹底的に初学者向けの内容とすることも確定事項でした。方針としては時系列青本と被るところもあったので、内容の重複が起こらないように調整しました。季節性や状態空間モデルの解説を入れることはここにも貢献しています。また、金融時系列にこだわらない様々なデータの例を取り上げることでも差別化しました。結果として、両方とも「Rで学ぶ初学者向けの時系列分析」の本なのに、まったく異なる本になったかと思います。

一般化状態空間モデルの推定として粒子フィルタを用いないことには大きな逡巡もありましたが、フィルタリングの基礎はカルマンフィルタでもある程度学ぶことができます。
必要最小限をまとめた書籍としてはこの構成がベストだったと信じます。

どの書籍とも異なるが、どの書籍にもつながる本。「初学者が最初に読む一冊」として必要な要素をまとめた本。そんな本を目指して隼時系列本を執筆しました。
隼時系列本を読んだ後に、他のどの本を読んでも新たな発見があるはずです。是非様々な書籍を読んでみてください。そして、様々なデータに触れてみてください。

隼時系列本のサポートページはこちらです。

更新履歴
2018年03月05日：新規作成。
2018年03月06日：古典的なモデルを過小評価するように見えたので、補足を追記。