Stanで推定する多変量時系列モデル
この記事では、複数の観測値があるが、状態は1つしかないモデルを推定します。状態空間モデルを用いてこれを達成します。RとStanという2つのソフトウェアの組み合わせを使ってモデルを推定します。コードはGitHubから参照できます。
以前にも『VARモデル』という多変量時系列モデルを紹介しましたが、それとは異なる状況のモデル化となります。先述のように状態空間モデルを用います。このモデルの基本的なことは『状態空間モデル』などの記事も参照してください。
この記事の例題はやや簡単すぎるきらいがあるため、最後により複雑なモデルを、文献を挙げて紹介します。
この記事はStan Advent Calendar 2018の10日目の記事となります。
詳細は「Stan Advent Calendar 2018」を参照してください。このリンクをたどると、Stanに関する様々な記事を読むことができます。
この記事は、文献が少ないテーマを扱うため、やや実験的な側面も含みます。MCMCの収束が悪くなることもありました(とはいえ添付コード・seedにおいてRhat<1.05となったのは確認済み)。誤りや改善点などあれば、ご指摘いただけますと幸いです。
目次
- 複数の観測値、一つの状態
- モデル1:データ生成
- モデル1:モデルの推定
- モデル1:推定結果の図示
- モデル2:データ生成
- モデル2:モデルの推定
- モデル2:推定結果の図示
- もっと複雑なモデルの紹介
1.複数の観測値、一つの状態
この記事では、複数の観測値があるが、状態は1つしかないモデルを推定します。状態空間モデルを用いてこれを達成します。状態空間モデルの基本事項は『状態空間モデル』などの記事を参照していただければと思います。まずはモデルの基本的な構造を説明します。
例えば、お客さんがAさん、Bさん…Jさんまで10人いたとします。10人のお客さんが各々商品を買ってくれます。一人のお客さんが毎日商品を購入するのが現実的でないならば、付き合いのあるお店ごとの売り上げデータだとか、ユーザーごとの月々のスマホゲームの課金額だとか、色々と考えてもらって良いかと思います。あくまでも話を進めるための例です。
売り上げは時系列データとして記録されています。売り上げデータは100時点分あります。10人×100時点で1000個の売り上げデータが記録されているわけです。
お客さんは、皆さん同じ商品(サービス)を対象にされています。そのため、程度の違いはあれ、多かれ少なかれ似たような変動を示します。例えば3月には全員がたくさん商品を購入して、5月には揃って商品の購入額が減るような感じです。あるいはサービスの品質が落ちたり、飽きられたりしても、みんな揃って売り上げが減ってしまうことでしょう。周期性を扱うと話がややこしくなるので、全体的な売り上げの傾向は、サービスの品質で決まるものと考えます。こういった目に見えないサービスの品質のようなものを状態と考えてモデル化を試みます。
状態空間モデルは、状態の変化の仕方と、観測値の得られ方の2つを分けてモデル化するのが特徴です。
状態の変化の仕方には様々考えられますが、まずは最も簡単な『ランダムウォーク』という構造を想定することにします。状態の変遷は『ローカルレベルモデル』と同じ物を想定していることになります。もちろんローカル線形トレンドモデルなどと同様の構造を想定することもできますが、話を簡単にするため、ランダムウォークを仮定します。
続いて観測値の得られ方を考えます。全体的に似たような傾向を示すとは言え、10人のお客さんごとに、売り上げ額は多少変わります。お客さんごとの違いをどのように表現するかはとても難しくて重要な問題ですが、この記事では2つのモデルを想定します。
- モデル1:たくさん買ってくれるお客さん、あまり買ってくれないお客さんとに分かれている
- その程度は時間によって変化しない
- たくさん買ってくれるお客さんはずっと買い続けてくれる
- 購入額が少ないお客さんも、ずっとそのまま変わらない
- お客さんごとの売り上げの違いは、平均0で任意の分散を持つ正規分布で表現できる(一般化線形混合モデルにおけるランダム効果をイメージしてください)
- その程度は時間によって変化しない
- モデル2:モデル1に広告の効果を加える
- 広告の効果は、時間によって変化しない
- (モデルと直接の関係はないけど)広告の出し方の補足
- 最初は、すべてのお客さんにランダムに広告を打つ
- 後半は、あまり商品を買ってくれないお客さんだけに広告を打つ
- すなわち、お客さんによって広告の出し具合が変わる
モデル1では、お客さんの違いは「平均しちゃうと0になる」ことを想定しています。そのため、無理に複雑なモデルを推定しなくても、10人の売り上げデータを平均すると、お客さんごとの違いをある程度排除した状態の推定値を得ることができます。少々単純すぎるきらいがありますが、スタート地点としてはちょうどいいかなと思ったので紹介します。
モデル2では、お客さんごとの違いが大きくなります。広告をたくさん出したお客さんもいれば、広告をほとんど目にしていないお客さんもいるからです。単なる売り上げの平均値をとったものと、サービスの品質という状態は、乖離することが想像できます。
お客さん全員の売り上げの平均値だけを議論すると、お客さん固有の情報を無視してしまうことになります。一方で、お客さん別に、まったく異なるモデルを推定してしまっては「同じ商品(サービス)が対象とされている。だから売り上げの変動は似たようなものになるはずだ」という想定を無視してしまうことになります。両方のやり方のいいとこどりをしたいな、というのが、今回のモデルを用いるモチベーションとなります。
補足:その他の多変量時系列モデル
この記事で紹介するモデルが「標準的なモデルなのだ」と勘違いされると困るので、ごく簡単に補足します。様々な多変量時系列モデルがありうるし、その目的も様々です。
多変量時系列モデルの代表は『VARモデル』です。詳しくはリンク先の記事を参照してください。
VARモデルでは「各々の観測値が、互いに影響を及ぼしあっている」ことを想定します。例えばAさんがたくさん商品を購入したら、Bさんもたくさん買ってくれる、と言った関係性があることを想定します。SNSなどでユーザーごとのやり取りがある場合ですと、このような可能性もあるかもしれません。この記事で紹介しているモデルは、互いのユーザーが影響を及ぼしあうことは想定していません。
VARモデルは例えば、マクロ経済の指標などにおいて、互いの関連性を議論するときなどに使われます。消費と収入の関係性をモデル化するような場合です。消費が増えたら、お店の売り上げが増えるので、収入も増えるかもしれない、ということは、なんとなく想像できますね。
また、この記事の最後に、他のモデルの例を紹介します。観測値の種類を増やすことで、状態をさらに精度よく推定したい、と言ったモチベーションで、多変量のモデルが使われることもあるようです。
2.モデル1:データ生成
コードはGitHubから参照できます。
10人×100時点の売上データを対象として分析を試みます。このデータはシミュレーションで作ることにします。この方が、モデルの構造を理解しやすいと思ったからです。
実際にデータを生成する前に、ライブラリを読み込みます。Stanに関わるものだけでなく、データの整形や図示のためのライブラリも入れてあります。この記事では断りなくパイプ演算子を使いますが、苦手な方は雰囲気だけつかんでもらっても良いかと思います。また、流行りの(?)gghighlightを使ってみたかったので、それも入れてあります。
library(tidyverse)
library(magrittr)
library(ggfortify)
library(gghighlight)
library(rstan)
library(bayesplot)
# 計算の高速化
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
続いて、シミュレーションにおけるパラメタの設定をまとめてしておきます。また、状態xや観測値yをNAが格納された行列として準備しておきます。
## パラメタの設定
N <- 100 # 期間
user_num <- 10 # ユーザー数
x_0 <- 200 # 状態初期値
s_w <- 20 # 過程誤差の標準偏差
s_v <- 30 # 観測誤差の標準偏差
s_r <- 50 # ランダム効果の標準偏差
x <- matrix(nrow = N) # 全ユーザー共通の状態
r <- matrix(ncol = user_num) # ユーザーごとのランダム効果
y <- matrix(nrow = N, ncol = user_num) # ユーザーごとの売り上げ
# わかりやすくするため、列名を付けておく
colnames(x) <- "state"
colnames(y) <- LETTERS[1:10]
colnames(r) <- LETTERS[1:10]
こんな感じの結果になっています。ここのNAを、シミュレーションをして埋めていくわけですね。
> # 状態
> head(x, n = 3)
state
[1,] NA
[2,] NA
[3,] NA
> # 観測値
> head(y, n = 3)
A B C D E F G H I J
[1,] NA NA NA NA NA NA NA NA NA NA
[2,] NA NA NA NA NA NA NA NA NA NA
[3,] NA NA NA NA NA NA NA NA NA NA
> # ユーザー別の売り上げ増減効果
> r
A B C D E F G H I J
[1,] NA NA NA NA NA NA NA NA NA NA
まずは、ユーザー別の売り上げ増減効果から作っていきます。
# 乱数の種
set.seed(2)
# ユーザーごとのランダム効果の生成
r[] <- rnorm(n = user_num, mean = 0, sd = s_r)
結果はこちら。
> r %>% round(1)
A B C D E F G H I J
[1,] -44.8 9.2 79.4 -56.5 -4 6.6 35.4 -12 99.2 -6.9
続いて、状態と観測値をまとめて作成します。
# 状態の初期値
x[1,] <- rnorm(n = 1, mean = x_0, sd = s_w)
# 各時点(i)ごとにループを回して、状態を遷移させる
for(i in 2:N){
# 状態の遷移(ランダムウォーク仮定)
x[i,] <- rnorm(n = 1, mean = x[i-1], sd = s_w)
}
# 各時点(i)ごと、ユーザー(j)ごとにループを回す
for(i in 1:N){
for(j in 1:user_num){
# 「状態+ユーザー固有のランダム効果」を平均値として、
# 観測ノイズが加わって、観測値が得られる
y[i,j] <- rnorm(n = 1, mean = x[i]+r[j], sd = s_v)
}
}
結果はこちら。
> # 状態
> x %>% round(1) %>% head(n = 3)
state
[1,] 208.4
[2,] 228.0
[3,] 220.1
> # 10人の売り上げ時系列データ
> y %>% round(1) %>% head(n = 3)
A B C D E F G H I J
[1,] 132.7 210.1 301.9 192.6 221.3 228.7 280.7 230.8 310.8 177.9
[2,] 220.4 241.4 358.7 158.6 192.6 250.7 243.3 235.2 275.5 168.8
[3,] 196.0 239.3 325.7 103.1 252.5 262.8 286.5 231.7 382.7 169.6
このままでもStanでの推定は可能なのですが、データの特徴がわかりにくいかと思うので、図示することにします。
図示にはggplot2とgghighlightを使うのですが、その前にデータを整然データの形式に変換する必要があります。この作業が若干手間なので、tidyverseのライブラリ群を使って実装することにしました(パイプ演算子は使いすぎると可読性が逆に下がってしまうような気もしますが、コードが短くて済むのは間違いないです)。
本当は一発で済む変換なのですが、データ整形の流れをお伝えするために、わざと2つに分割して実装しています(モデル2ではまとめてやっつけてしまっています)。ついでに言うと、あまり効率の良いやり方ではないかもしれません。
> # データをまとめる
> sim_df <- y %>%
+ cbind(state = x) %>%
+ cbind(time = 1:100) %>%
+ data.frame
> # 観測値・状態・時点番号をまとめた結果
> sim_df %>% round(1) %>% head(n = 3)
A B C D E F G H I J state time
1 132.7 210.1 301.9 192.6 221.3 228.7 280.7 230.8 310.8 177.9 208.4 1
2 220.4 241.4 358.7 158.6 192.6 250.7 243.3 235.2 275.5 168.8 228.0 2
3 196.0 239.3 325.7 103.1 252.5 262.8 286.5 231.7 382.7 169.6 220.1 3
sim_dfだと、列名としてユーザーの名前が入っています。ユーザー名を取り出そうと思ったら、列名にアクセスしないといけないんですね。これは不便です。すべての情報がデータの「中身」に存在していた方が簡単です。その代わり、列名には「売り上げ」とか「ユーザー名」とか言った『どういうデータが中に格納されているのか』が一目でわかるように設定をしたいです。
こういう風な「データの構造(列名とか)と、データの意味(中に何が入っているか)が一致する」データの形式を整然データと呼びます(整然データについては外部リンクですが『整然データとは何か|Colorless Green Ideas』などを参照してください)。sim_dfを整然データに変換するコードは以下の通りです。
> # 整然データの形式にする
> sim_tidy <- sim_df %>%
+ gather(key = "name",
+ value = "sales",
+ factor_key = TRUE,
+ - time)
> # 結果
> summary(sim_tidy)
time name sales
Min. : 1.00 A :100 Min. :-17.33
1st Qu.: 25.75 B :100 1st Qu.:163.91
Median : 50.50 C :100 Median :221.80
Mean : 50.50 D :100 Mean :222.57
3rd Qu.: 75.25 E :100 3rd Qu.:280.39
Max. :100.00 F :100 Max. :481.65
(Other):500
> summary(sim_tidy$name)
A B C D E F G H I J state
100 100 100 100 100 100 100 100 100 100 100
> head(sim_tidy, n = 3)
time name sales
1 1 A 132.6859
2 2 A 220.3783
3 3 A 195.9826
timeという列には時点番号が、name列にはユーザー名や「状態(state)」と言った時系列の情報が、そしてsales列には売り上げデータが入っています。
整然データの形式にできれば、可視化するのは簡単です。gghighlightを使って、特定のユーザー(AさんとCさん)と状態の値をハイライトしました。
# 図示
ggplot(data = sim_tidy) +
ggtitle("シミュレーションにより生成された売り上げデータ(モデル1)") +
geom_line(aes(x = time, y = sales, color = name)) +
gghighlight(name == "state" | name == "A"| name == "C",
use_group_by = FALSE)

Aさんは常に売り上げが低めで、Cさんは逆に売り上げが常に高めとなっています。ユーザーの個性を認めつつ、全体の傾向を調べよう、というのが今回のテーマですね。
3.モデル1:モデルの推定
複数の観測値、一つの状態を持つモデル1を推定するStanコードは以下のようになります。シミュレーションとほとんど同じコードなので、説明は省略します。詳しくはコード内のコメントを参照してください。これを『ssm-user-sales.stan』という名前で保存します。
data {
int T; // データ取得期間の長さ
int user_num; // ユーザー数
matrix[T, user_num] y; // 観測値
}
parameters {
vector[T] x; // 状態の推定値
vector[user_num] r; // ユーザー毎のランダム効果
real<lower=0> s_w; // 過程誤差の標準偏差
real<lower=0> s_v; // 観測誤差の標準偏差
real<lower=0> s_r; // ランダム効果の標準偏差
}
model {
// 状態方程式に従い、状態が遷移する
for(i in 2:T) {
x[i] ~ normal(x[i-1], s_w);
}
// ランダム効果
r ~ normal(0, s_r);
// 観測方程式に従い、観測値が得られる
for(i in 1:T) {
for(j in 1:user_num) {
y[i, j] ~ normal(x[i] + r[j], s_v);
}
}
}MCMCを実行します。この辺りがわからない方は『Stanによるベイズ推定の基礎』などを参照してください。データをlistにまとめてから『stan』関数を実行します。
# データの準備
data_list_1 <- list(
y = y,
T = N,
user_num = user_num
)
# 多変量モデルの推定
malti_1 <- stan(
file = "ssm-user-sales.stan",
data = data_list_1,
seed = 1,
iter = 30000,
warmup = 10000,
thin = 10
)
収束はbayesplotパッケージの以下のコードで確認します。Rhat<1.05であるようです。
mcmc_rhat(rhat(malti_1))
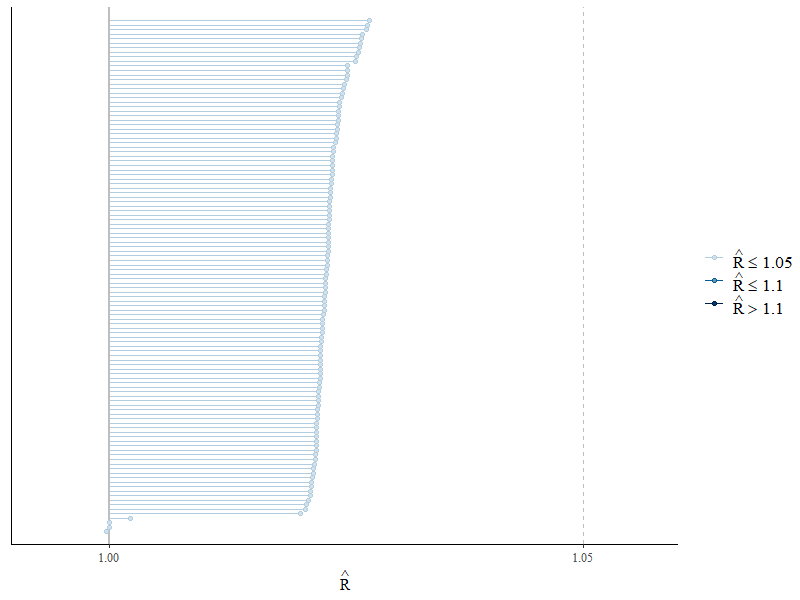
推定されたパラメタも、シミュレーションで想定したものと近いものになっています。ただし、MCMCのiterを増やさないとなかなか収束しませんでした。シミュレーションデータを変えても収束が悪くなることもあり、少し不安定だなと感じました。
> # モデル1の推定結果
> print(malti_1,
+ par = c("s_w", "s_v", "s_r", "lp__"),
+ probs = c(0.025, 0.5, 0.975))
Inference for Stan model: ssm-user-sales.
4 chains, each with iter=30000; warmup=10000; thin=10;
post-warmup draws per chain=2000, total post-warmup draws=8000.
mean se_mean sd 2.5% 50% 97.5% n_eff Rhat
s_w 24.81 0.02 2.19 20.84 24.66 29.40 8086 1
s_v 29.37 0.01 0.69 28.06 29.37 30.75 7975 1
s_r 58.48 0.43 17.49 35.75 55.04 102.87 1631 1
lp__ -4280.27 0.09 8.00 -4296.89 -4279.99 -4265.63 7771 1
4.モデル1:推定結果の図示
最後に、MCMCサンプルを整然データの形式に整形したのち、状態推定値などを図示します。まずはデータの整形から。
> # データの整形
> stan_df_1 <- malti_1 %>%
+ rstan::extract() %$% x %>%
+ apply(2, quantile, probs = c(0.025, 0.5, 0.975)) %>%
+ t() %>%
+ cbind(1:nrow(sim_df)) %>%
+ data.frame
> # 列名の変更
> colnames(stan_df_1) <- c("lwr", "fit", "upr", "time")
> # 結果
> head(stan_df_1, n = 3)
lwr fit upr time
1 190.4312 230.2643 275.1182 1
2 195.3581 235.0489 279.1538 2
3 201.6797 240.9920 285.1719 3
図示します。
・・・どうやって図示しようか悩んだんですが、gghighlightに上書きするように、状態推定値の中央値と95%ベイズ信用区間を載せました。しかし、ややダサかったかもしれません。とりあえず、シミュレーションで生成した状態と、MCMCで推定された状態推定値が近い値になっていることは確認できます。
# 図示
ggplot(data = sim_tidy) +
ggtitle("推定結果(モデル1)") +
geom_line(aes(x = time, y = sales, color = name)) +
gghighlight(name == "state", use_group_by = FALSE) +
geom_line(data = stan_df_1,
aes(x = time, y = fit), size = 1.2) +
geom_ribbon(data = stan_df_1,
aes(x = time, ymin = lwr, ymax = upr), alpha = 0.3)
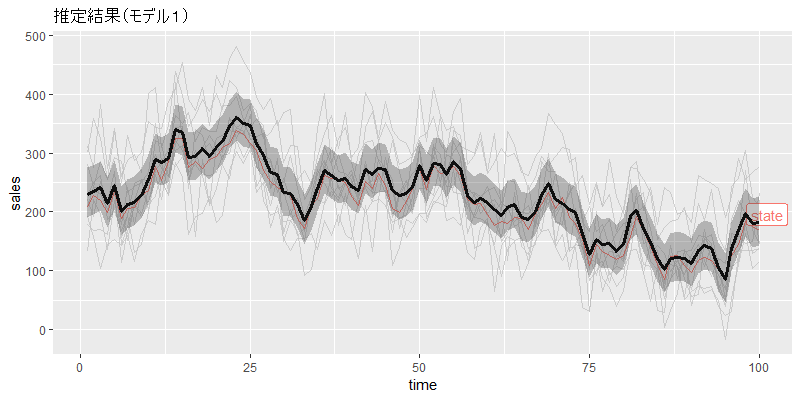
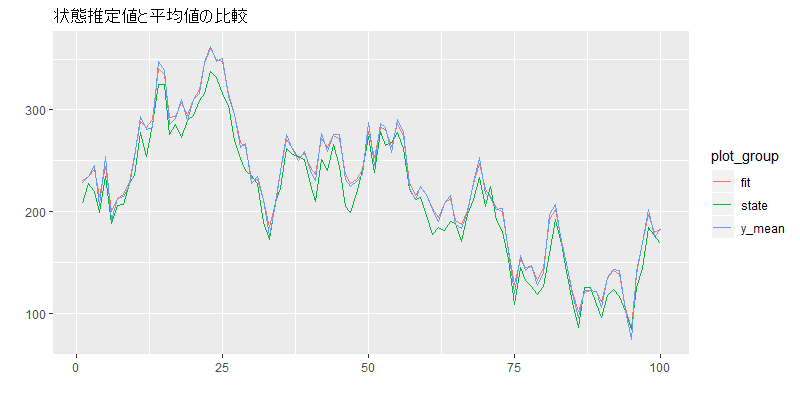
ただし、今回のような単純なモデルでは、10人の売り上げの平均値と、状態の推定値はほぼ同じになります。
# 状態と比較
cbind(y_mean = apply(y, 1,mean),
state = x,
fit = stan_df_1[,"fit"]) %>%
ts() %>%
autoplot(facet = F, main = "状態推定値と平均値の比較")
5.モデル2:データ生成
単純すぎるモデルですとあまり面白くないので、説明変数を追加することにします。ユーザーごとに異なる頻度で広告を打つことにします。
まずはモデル1と同じようにパラメタなどを設定しておきます。ただし、100行×10列の「広告実施フラグ」を用意しておきます。
## パラメタの設定
N <- 100 # 期間
user_num <- 10 # ユーザー数
x_0 <- 200 # 状態初期値
s_w <- 20 # 過程誤差の標準偏差
s_v <- 30 # 観測誤差の標準偏差
s_r <- 50 # ランダム効果の標準偏差
b_ad <- 100 # 広告による売り上げ増加効果
x <- matrix(nrow = N) # 全ユーザー共通の状態
r <- matrix(ncol = user_num) # ユーザーごとのランダム効果
y <- matrix(nrow = N, ncol = user_num) # ユーザーごとの売り上げ
ad_flag <- matrix(nrow = N, ncol = user_num) # 0なら広告なし。1で広告あり。
# わかりやすくするため、列名を付けておく
colnames(x) <- "state"
colnames(y) <- LETTERS[1:10]
colnames(ad_flag) <- LETTERS[1:10]
colnames(r) <- LETTERS[1:10]
結果はこちら。
> # 状態
> head(x, n = 3)
state
[1,] NA
[2,] NA
[3,] NA
> # 観測値
> head(y, n = 3)
A B C D E F G H I J
[1,] NA NA NA NA NA NA NA NA NA NA
[2,] NA NA NA NA NA NA NA NA NA NA
[3,] NA NA NA NA NA NA NA NA NA NA
> # ユーザー別の売り上げ増減効果
> r
A B C D E F G H I J
[1,] NA NA NA NA NA NA NA NA NA NA
> # ユーザー別の広告送付実績
> head(ad_flag, n = 3)
A B C D E F G H I J
[1,] NA NA NA NA NA NA NA NA NA NA
[2,] NA NA NA NA NA NA NA NA NA NA
[3,] NA NA NA NA NA NA NA NA NA NA
実際に乱数を生成して、架空の売り上げデータなどを作っていきます。まずはユーザーごとに異なるランダム効果を生成します。
> # 乱数の種
> set.seed(2)
> # ユーザーごとのランダム効果の生成
> r[] <- rnorm(n = user_num, mean = 0, sd = s_r)
> # AさんとDさんは売り上げがとても低い
> # HさんとJさんもちょっと低い
> round(r, 1)
A B C D E F G H I J
[1,] -44.8 9.2 79.4 -56.5 -4 6.6 35.4 -12 99.2 -6.9
上記の結果を見ると、A,D,H,Jさんは、平均(0)よりも、売り上げが少なくなっているようです。そこで、この4人に対して重点的に広告を打った、と考えます。
まず、最初の50時点では、全体の3割ほどに、ランダムに広告を入れます。そして、最後の50時点では、A,D,H,Jさんにだけ広告を配信します。
> # 全体的にランダムに広告をいれる
> ad_flag[1:50,] <- sample(c(0,1),
+ size = N*user_num / 2,
+ replace = T,
+ prob = c(0.7, 0.3))
> # 広告配信率
> mean(ad_flag[1:50,])
[1] 0.302
> # 最後の50日は、A,D,H,Jさんはずっと広告を打つ。他は広告なし
> ad_flag[51:100,] <- 0
> ad_flag[51:100, c("A", "D", "H", "J")] <- 1
> ad_flag
A B C D E F G H I J
[1,] 0 0 0 1 0 1 0 1 1 0
[2,] 0 0 0 0 1 1 0 0 0 0
・・・中略・・・
[48,] 0 0 1 0 0 0 0 0 1 0
[49,] 0 1 0 0 1 1 1 0 0 0
[50,] 0 0 0 0 0 0 0 1 0 1
[51,] 1 0 0 1 0 0 0 1 0 1
[52,] 1 0 0 1 0 0 0 1 0 1
・・・中略・・・
[99,] 1 0 0 1 0 0 0 1 0 1
[100,] 1 0 0 1 0 0 0 1 0 1
後は、モデル1と同じようにシミュレーションを行います。観測値が得られる際、広告の影響を加味することを忘れないようにします。
# 乱数の種
set.seed(2)
# 状態の初期値
x[1, ] <- rnorm(n = 1, mean = x_0, sd = s_w)
# 各時点(i)ごとにループを回して、状態を遷移させる
for(i in 2:N){
# 状態の遷移(ランダムウォーク仮定)
x[i,] <- rnorm(n = 1, mean = x[i-1], sd = s_w)
}
# 各時点(i)ごと、ユーザー(j)ごとにループを回す
for(i in 1:N){
for(j in 1:user_num){
# 「状態+ユーザー固有のランダム効果+広告効果」を平均値として、
# 観測ノイズが加わって、観測値が得られる
y[i,j] <- rnorm(n = 1, mean = x[i]+r[j]+ad_flag[i, j]*b_ad, sd = s_v)
}
}
こんな感じの売り上げデータになっています。
> # 10人の売り上げ時系列データ
> y %>% round(1) %>% head(n = 3)
A B C D E F G H I J
[1,] 169.4 199.1 252.0 203.1 152.2 350.1 245.7 330.3 368.6 164.6
[2,] 110.1 187.5 279.3 170.0 298.7 306.1 258.1 208.2 288.2 155.3
[3,] 309.9 230.9 448.2 148.1 182.2 340.3 232.8 224.7 265.0 158.3
続いて、観測値と状態をまとめたうえで、整然データに整形します。
# 整然データの形式にする
sim_tidy <- y %>%
cbind(state = x) %>%
cbind(time = 1:100) %>%
data.frame %>%
gather(key = "name",
value = "sales",
factor_key = TRUE,
- time)
こんな結果になっています。
> # 結果
> summary(sim_tidy$name)
A B C D E F G H I J state
100 100 100 100 100 100 100 100 100 100 100
> head(sim_tidy, n = 3)
time name sales
1 1 A 169.4498
2 2 A 110.0915
3 3 A 309.9059
状態と、Dさん、Iさんの売り上げを図示します。
# 図示
ggplot(data = sim_tidy) +
ggtitle("シミュレーションにより生成された売り上げデータ(モデル2)") +
geom_line(aes(x = time, y = sales, color = name)) +
gghighlight(name == "state" | name == "D"| name == "I",
use_group_by = FALSE)
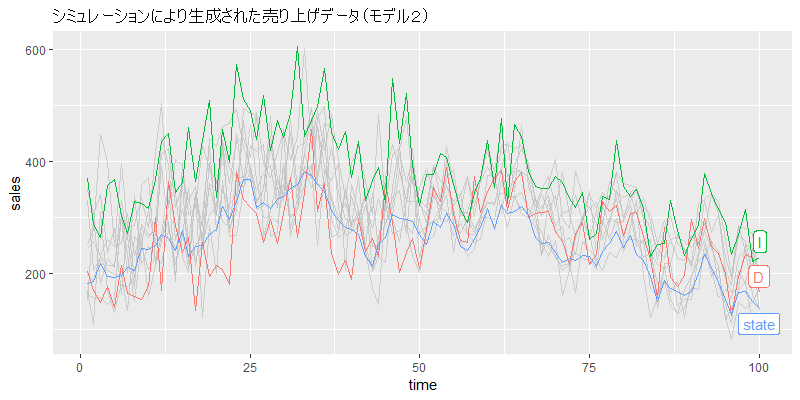
グラフを見ると、最初は売り上げが低かったDさんですが、50日以降は広告をたくさん出したので、売り上げが増えていることがわかります。一方のIさんは、50日以降は広告が配信されていないので、Dさんとほぼ同じ売り上げになっています。
6.モデル2:モデルの推定
説明変数付きのモデルを、Stanで実装します。『ssm-user-sales-ad.stan』という名称で保存しておきます。dataやparametersブロックに広告に関する1行を追加したうえで、観測方程式に『ad_flag[i,j]*b_ad』という広告の効果を入れます。他はモデル1と同じです。
data {
int T; // データ取得期間の長さ
int user_num; // ユーザー数
matrix[T, user_num] y; // 観測値
matrix[T, user_num] ad_flag; // ユーザーごと広告フラグ
}
parameters {
vector[T] x; // 状態の推定値
vector[user_num] r; // ユーザー毎のランダム効果
real<lower=0> s_w; // 過程誤差の標準偏差
real<lower=0> s_v; // 観測誤差の標準偏差
real<lower=0> s_r; // ランダム効果の標準偏差
real b_ad; // 広告による売り上げ増加効果
}
model {
// 状態方程式に従い、状態が遷移する
for(i in 2:T) {
x[i] ~ normal(x[i-1], s_w);
}
// ランダム効果
r ~ normal(0, s_r);
// 観測方程式に従い、観測値が得られる
for(i in 1:T) {
for(j in 1:user_num) {
y[i, j] ~ normal(x[i] + r[j] + ad_flag[i,j]*b_ad, s_v);
}
}
}
続いて、モデル1と同じようにMCMCを実行します。こちらも収束しなかったので、やや多めのiterを設定しています。
# データの準備
data_list_2 <- list(
y = y,
ad_flag = ad_flag,
T = N,
user_num = user_num
)
# 多変量モデルの推定
malti_2 <- stan(
file = "ssm-user-sales-ad.stan",
data = data_list_2,
seed = 1,
iter = 30000,
warmup = 10000,
thin = 10
)
Rhat<1.05になっていることを確認します(トレースプロットはあまりきれいではなかったので、もう少し工夫の余地はあったかもしれません)。
mcmc_rhat(rhat(malti_2))
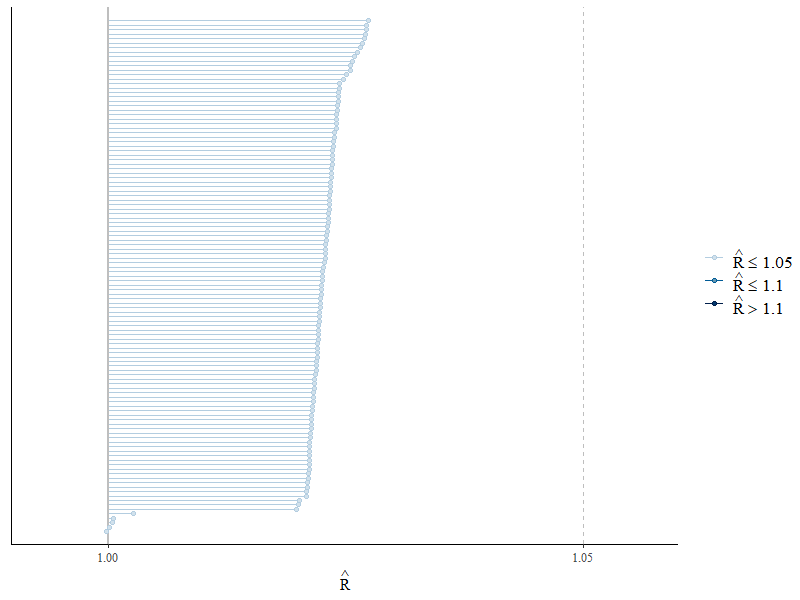
推定されたパラメタは以下の通りです。シミュレーションで設定した値と近いものになっています。
> # 多変量モデルの推定結果
> print(malti_2,
+ par = c("s_w", "s_v", "s_r", "b_ad", "lp__"),
+ probs = c(0.025, 0.5, 0.975))
Inference for Stan model: ssm-user-sales-ad.
4 chains, each with iter=30000; warmup=10000; thin=10;
post-warmup draws per chain=2000, total post-warmup draws=8000.
mean se_mean sd 2.5% 50% 97.5% n_eff Rhat
s_w 25.95 0.03 2.33 21.77 25.82 30.84 7623 1
s_v 29.44 0.01 0.70 28.11 29.41 30.85 7596 1
s_r 58.47 0.35 17.20 35.92 54.89 100.78 2397 1
b_ad 101.34 0.03 2.37 96.59 101.34 105.87 7790 1
lp__ -4286.67 0.09 8.03 -4303.55 -4286.27 -4272.14 7391 1
7.モデル2:推定結果の図示
最後に、状態推定値を図示します。モデル1と同じやり方で行きます。MCMCサンプルの整形と図示をまとめて行います。
# データの整形
stan_df_2 <- malti_2 %>%
rstan::extract() %$% x %>%
apply(2, quantile, probs = c(0.025, 0.5, 0.975)) %>%
t() %>%
cbind(1:nrow(sim_df)) %>%
data.frame
# 列名の変更
colnames(stan_df_2) <- c("lwr", "fit", "upr", "time")
# 図示
ggplot(data = sim_tidy) +
ggtitle("推定結果(モデル1)") +
geom_line(aes(x = time, y = sales, color = name)) +
gghighlight(name == "state", use_group_by = FALSE) +
geom_line(data = stan_df_2,
aes(x = time, y = fit), size = 1.2) +
geom_ribbon(data = stan_df_2,
aes(x = time, ymin = lwr, ymax = upr), alpha = 0.3)
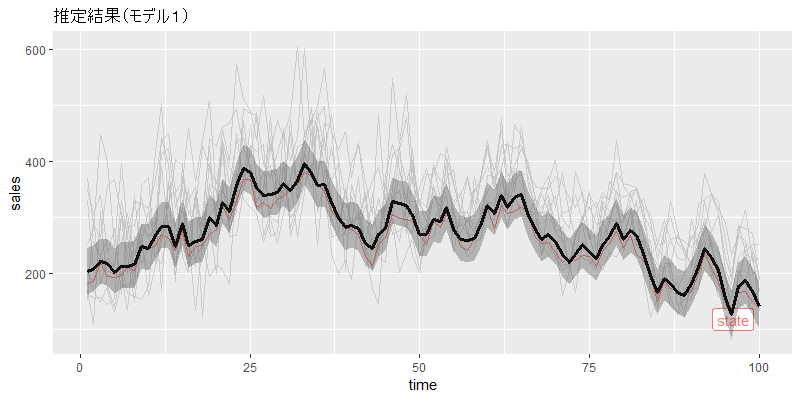
モデル1と違って、状態推定値は、単に売り上げの平均をとったものとは異なるようです。広告の影響を取り除いて、より正確な状態の推定値が得られました。
# 状態と比較
cbind(y_mean = apply(y, 1,mean),
state = x,
fit = stan_df_2[,"fit"]) %>%
ts() %>%
autoplot(facet = F, main = "状態推定値と平均値の比較")
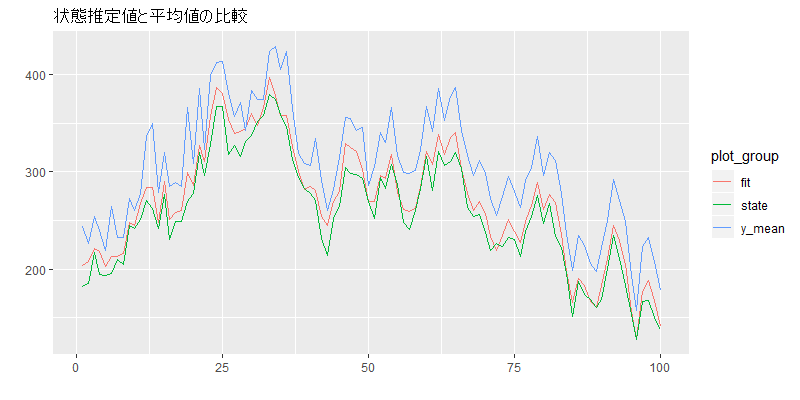
単純なモデルではありますが「複数の観測値、1つの状態」のモデルの構造と実装例を挙げました。一連の分析はここで終わります。
8.もっと複雑なモデルの紹介
■浅田 正彦, 長田 穣, 深澤 圭太, 落合 啓二 (2014) 『状態空間モデルを用いた階層ベイズ推定法によるキョン(Muntiacus reevesi) の個体数推定』
上記論文は無料で読むことができます。WinBUGSを使った実装コードも掲載されているので勉強になります。詳細は論文を参照してください。上記論文は、キョンという動物の個体数を推定したり、個体群増加率を推定したりしています。
個体数を推定するときに、調査を行うわけですが、調査データは1種類ではありません。糞粒数・発見個体数・捕獲個体数の3種類の観測値を使ってモデルを構築しています。動物がいないところで糞粒だけが無から生まれることはないですね。様々な観測データを使ってそれを統合することで、単一の指標を用いた場合よりも精度よく、個体数などを推定しよう、という試みのようです。
状態の変化のモデルも、観測値が得られるプロセスも、このブログのものとは比較にならないほど複雑です。
■久保拓弥, 重田麻衣 , 亀崎直樹(2009)『ウミガメ上陸数のベイズ統計モデリング』
上記はポスター発表のようです。年別・地点別のウミガメ上陸個体数データを分析した例です。ウミガメ全体として共通する状態を持ちつつ、年別・地点別に異なるノイズが加わって、上陸個体数データが得られていると考えています。
トレンドの構造や観測誤差の加わり方が少し違いますが、この記事で扱ったものと少し似ているかもしれません。
■松浦(2016)『StanとRでベイズ統計モデリング』
ベイズ統計モデリングの分野では有名な書籍です。分析例は載っていませんが、モデルの拡張の一例として、多変量時系列モデルのモデル式が掲載されています。
この記事では1つの状態を想定していましたが、書籍中ではユーザーごとに個別の状態があることを想定しているようです。
更新履歴
2018年12月10日:新規作成

