状態空間モデルをStanで推定するときの収束を良くするコツ
この記事では、状態空間モデルをStanで推定するときの収束を良くするコツを説明します。
コードはGitHubから参照できます。
状態空間モデルは説明能力が高く、データに合わせて柔軟に構造を変えることができます。しかし、あまりに複雑な構造を指定すると、結果が収束しないこともしばしばあります。
収束が悪い時には、弱情報事前分布を指定したり、MCMC実行時の設定を変える(iterやwarmupを増やす等)で対応することが多いと思います。こちらの方法で多くの場合は解決しますが、複雑なモデルですと、そもそものStanコードの実装の方法から変えた方が良いかもしれません。
この記事では、状態空間モデルの収束を良くするために、Stanコードの書き方を工夫するやり方を紹介します。
良いやり方は無いかなと調べていたところ『Bayesian structural time series modeling』という記事を見つけました。上記の記事で提案されている方法を参考にしています(コードは少し変えました)。
この記事の方法を使うと、収束が良くなることがあるようですが、正直コードの可読性は下がってしまいます。ミスが発生する可能性が増えるので注意してください。
万が一、この記事の内容に誤りがあった場合は、コメントやメールなどでご連絡いただければ幸いです。
この記事では、読者がすでにR言語やStan、そして状態空間モデルの基本について知っていることを前提としています。これらに関する基本事項がわからない方は、例えば拙著『RとStanではじめる ベイズ統計モデリングによるデータ分析入門』などを参照してください。一部のコードは、この本からの引用となります。
この記事はStan Advent Calendar 2019の14日目の記事となります。
詳細は「Stan Advent Calendar 2019」を参照してください。このリンクをたどると、Stanに関する様々な記事を読むことができます。
スポンサードリンク
目次
- シミュレーションデータの作成
- 素朴な実装
- ローカルレベルモデル
- ローカル線形トレンドモデル
- 収束のための工夫をした実装
- 基本方針
- ベクトル化したローカルレベルモデル
- 再パラメータ化したローカルレベルモデル
- 再パラメータ化したローカル線形トレンドモデル
1.シミュレーションデータの作成
まずは、分析対象となるデータを作成します。ローカル線形トレンドモデルに従う乱数を生成します。
コードはGitHubから参照できます。
## パラメタの設定
N <- 200 # 期間
mu_0 <- 300 # 状態初期値
delta_0 <- -2 # ドリフト成分初期値
sd_w <- 2 # 水準成分の変動の大きさを表す標準偏差
sd_z <- 0.2 # ドリフト成分の変動の大きさを表す標準偏差
sd_v <- 20 # 観測誤差の標準偏差
## 乱数の生成
set.seed(1) # 乱数の種
mu <- numeric(N) # 状態(水準+ドリフト)
delta <- numeric(N) # 状態(ドリフト)
y <- numeric(N) # 観測値
# 状態の1時点目の値を生成
mu[1] <- rnorm(n = 1, mean = mu_0, sd = sd_w)
delta[1] <- rnorm(n = 1, mean = delta_0, sd = sd_z)
# 状態の遷移と観測値の生成
for(i in 1:N){
mu[i + 1] <- rnorm(n = 1, mean = mu[i] + delta[i], sd = sd_w)
delta[i + 1] <- rnorm(n = 1, mean = delta[i], sd = sd_z)
y[i] <- rnorm(n = 1, mean = mu[i], sd = sd_v)
}
シミュレーションデータの折れ線グラフを描きます。
# シミュレーションデータの時系列グラフ y %>% ts() %>% autoplot(main = "シミュレーションデータ")
最初は全体的に減少傾向にあるデータですが、そのあとで上昇トレンドに変化していることがわかります。
最後に、後で使いやすくするためにlistにまとめておきます。
# データをlistにまとめる data_list_1 <- list(T = N, y = y)
2.素朴な実装
先ほど作成したシミュレーションデータを対象として、まずは素朴な実装を行ったStanコードでモデルを推定します。
ローカルレベルモデル
まずはローカルレベルモデルを推定します。シミュレーションデータはローカル線形トレンドモデルに従っているので、ローカルレベルモデルではちょっと力不足なのですが、コードが短くて簡単なため載せておきます。
以下のコードは拙著『RとStanではじめる ベイズ統計モデリングによるデータ分析入門』からの引用です。『local-level.stan』というファイル名称で保存されているとします。
data {
int T; // データ取得期間の長さ
vector[T] y; // 観測値
}
parameters {
vector[T] mu; // 状態の推定値(水準成分)
real<lower=0> s_w; // 過程誤差の標準偏差
real<lower=0> s_v; // 観測誤差の標準偏差
}
model {
// 状態方程式に従い、状態が遷移する
for(t in 2:T) {
mu[t] ~ normal(mu[t-1], s_w);
}
// 観測方程式に従い、観測値が得られる
for(t in 1:T) {
y[t] ~ normal(mu[t], s_v);
}
}
こちらでMCMCを実行すると、収束に関するワーニングが出ました。
> # ローカルレベルモデル > mod_ll <- stan( + file = "local-level.stan", + data = data_list_1, + seed = 1 + ) Warning messages: 1: There were 4 chains where the estimated Bayesian Fraction of Missing Information was low. See http://mc-stan.org/misc/warnings.html#bfmi-low 2: Examine the pairs() plot to diagnose sampling problems 3: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable. Running the chains for more iterations may help. See http://mc-stan.org/misc/warnings.html#bulk-ess
MCMCの結果は以下のようになっています。
Rhatは1.1未満ですが、ワーニングがあるので、改善の余地はありそうです。
> print(mod_ll, pars = c("s_w", "s_v"))
Inference for Stan model: local-level.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
s_w 4.89 0.06 0.94 3.38 4.22 4.8 5.45 6.95 238 1.02
s_v 18.51 0.02 1.07 16.50 17.80 18.5 19.22 20.60 3021 1.00
ローカル線形トレンドモデル
続いてローカル線形トレンドモデルです。ローカル線形トレンドモデルは、説明力の高い優れたモデルですが、経験上、収束しにくいように思います。
以下のコードは拙著『RとStanではじめる ベイズ統計モデリングによるデータ分析入門』のサンプルコードを一部改変したものです。『local-linear-trend.stan』というファイル名称で保存されているとします。
data {
int T; // データ取得期間の長さ
vector[T] y; // 観測値
}
parameters {
vector[T] mu; // 水準+ドリフト成分の推定値
vector[T] delta; // ドリフト成分の推定値
real<lower=0> s_w; // 水準成分の変動の大きさを表す標準偏差
real<lower=0> s_z; // ドリフト成分の変動の大きさを表す標準偏差
real<lower=0> s_v; // 観測誤差の標準偏差
}
model {
// 状態方程式に従い、状態が遷移する
for(t in 2:T) {
mu[t] ~ normal(mu[t-1] + delta[t-1], s_w);
delta[t] ~ normal(delta[t-1], s_z);
}
// 観測方程式に従い、観測値が得られる
for(t in 1:T) {
y[t] ~ normal(mu[t], s_v);
}
}
こちらのコードを実行すると、ワーニングが多く出ます。
> # ローカル線形トレンドモデル > mod_llt <- stan( + file = "local-linear-trend.stan", + data = data_list_1, + seed = 1 + ) Warning messages: 1: There were 655 transitions after warmup that exceeded the maximum treedepth. Increase max_treedepth above 10. See http://mc-stan.org/misc/warnings.html#maximum-treedepth-exceeded 2: There were 4 chains where the estimated Bayesian Fraction of Missing Information was low. See http://mc-stan.org/misc/warnings.html#bfmi-low 3: Examine the pairs() plot to diagnose sampling problems 4: The largest R-hat is 1.25, indicating chains have not mixed. Running the chains for more iterations may help. See http://mc-stan.org/misc/warnings.html#r-hat 5: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable. Running the chains for more iterations may help. See http://mc-stan.org/misc/warnings.html#bulk-ess 6: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable. Running the chains for more iterations may help. See http://mc-stan.org/misc/warnings.html#tail-ess
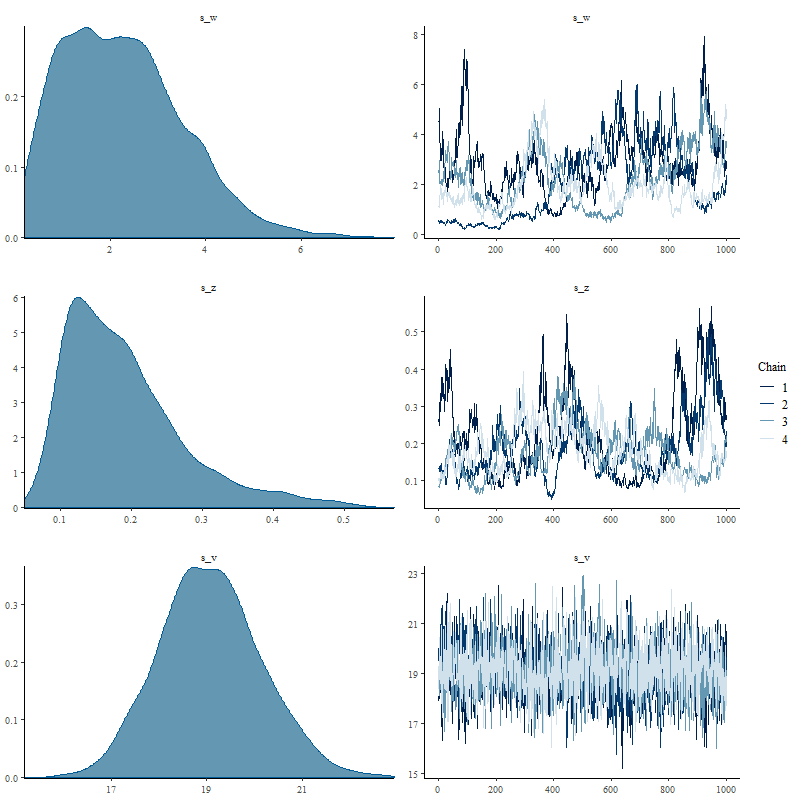
Rhatも1.1を超えており、収束したとは言えない状況です。
> print(mod_llt, pars = c("s_w", "s_z", "s_v"))
Inference for Stan model: local-linear-trend.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
s_w 2.27 0.27 1.25 0.37 1.29 2.14 3.05 5.03 22 1.20
s_z 0.19 0.01 0.08 0.08 0.13 0.17 0.23 0.42 39 1.04
s_v 19.08 0.04 1.08 17.07 18.35 19.05 19.77 21.28 761 1.01
トレースプロットを見ても、問題があるのがわかります。
# 事後分布の可視化
mcmc_combo(mod_llt, pars = c("s_w", "s_z", "s_v"))
誤解の無いように記しておくと、先のStanコードに大きな問題があるわけではないです。
素朴な実装ですし、初学者の方が最初に状態空間モデルの実装をする場合は、こちらの素朴な実装から入るべきだと思います。
データを作成したシミュレーションのコードを比較してもらうとわかるように、こちらの実装は「データの生成過程をそのまま」コードで表現できています。ベイズ統計モデリングの勉強という意味では、むしろこちらの素朴な実装を使う方が好ましいと思います。収束を良くするためのコードは、それなりにテクニカルな実装になります。
また、今回はあえてワーニングがたくさん出るように、何の工夫もせずに実行させてあります。上記の素朴なStanコードであっても、iterやwarmup、thinを増やしたり、弱情報事前分布を指定したりすることで、収束を改善させることができます(拙著ではその方法を使っていました)。
とはいえ、この記事のテーマはStanコードの書き方を工夫することで収束を良くするということです。
あえてiterやwarmupはそのままにして、収束を改善することを試みます。
スポンサードリンク
3.収束のための工夫をした実装
基本方針
Stanコードを修正する基本的な方針は2つあります。
まずはベクトル化をすることです。ベクトル化というのは少し難しいように聞こえる用語ですが、forループをやめて実装するイメージです。後ほど具体例を挙げます。
ただし、ベクトル化しても、収束がすぐに良くなるわけではありません。
そのうえで再パラメータ化をします。再パラメータ化がキモで、これで収束を良くします。
再パラメータ化をするとサンプリングが遅くなることもあるので、その点は注意が必要です。
再パラメータ化も、言葉では説明が難しいので、実際のコードを後ほど紹介します。
ベクトル化したローカルレベルモデル
まずはローカルレベルモデルのStanコードをベクトル化します。
『local-level-vec.stan』というファイル名で保存しておきます。
data {
int T; // データ取得期間の長さ
vector[T] y; // 観測値
}
parameters {
vector[T] mu; // 状態の推定値(水準成分)
real<lower=0> s_w; // 過程誤差の標準偏差
real<lower=0> s_v; // 観測誤差の標準偏差
}
model {
// 状態方程式に従い、状態が遷移する
mu[2:T] ~ normal(mu[1:T-1], s_w);
// 観測方程式に従い、観測値が得られる
y ~ normal(mu, s_v);
}
modelブロックのみ変更があります。
まずは状態方程式です。
muの2時点目は、平均値が『muの1時点目』である正規分布から得られます。
muのT時点目は、平均値が『muのT-1時点目』である正規分布から得られます。
これをまとめてmu[2:T] ~ normal(mu[1:T-1], s_w);としています。
観測方程式はさらに短いコードになっています。
y ~ normal(mu, s_v);です。長さが同じなので、角カッコを使って添え字を指定する必要もありません(添え字を入れても別に良い)。
ベクトル化をすることで、コードが短くなりました。実効速度が速くなることもあります。
ただし、収束に関するワーニングは引き続き出てきているようです。
> mod_ll_vec <- stan( + file = "local-level-vec.stan", + data = data_list_1, + seed = 1 + ) Warning messages: 1: There were 4 chains where the estimated Bayesian Fraction of Missing Information was low. See http://mc-stan.org/misc/warnings.html#bfmi-low 2: Examine the pairs() plot to diagnose sampling problems 3: Bulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable. Running the chains for more iterations may help. See http://mc-stan.org/misc/warnings.html#bulk-ess
再パラメータ化したローカルレベルモデル
続いて再パラメータ化をしたローカルレベルモデルのコードを載せます。『local-level-remodeling.stan』という名称で保存しておきます。
data {
int T; // データ取得期間の長さ
vector[T] y; // 観測値
}
parameters {
real<lower=0> s_w; // 過程誤差の標準偏差
real<lower=0> s_v; // 観測誤差の標準偏差
vector[T] mu_err; // 水準成分の増減量
}
transformed parameters {
// transformed parametersで実際の水準成分を得る
vector[T] mu; // 水準成分の推定値
// 1時点目
mu[1] = mu_err[1];
// 2時点目以降
for (t in 2:T) {
// 標準偏差1の正規乱数に、s_wをかけて実際の過程誤差としている
mu[t] = mu[t-1] + s_w * mu_err[t];
}
}
model {
// mu_err[1]は、無情報事前分布を指定
// mu_err[2]以降は、標準偏差1の正規乱数を得る
mu_err[2:T] ~ normal(0,1);
// 観測方程式
y ~ normal(mu, s_v);
}
ベクトル化したコードと比較すると、dataブロック以外はすべて変わっています。
まず、parametersブロックから、状態推定値muがなくなりました。その代わりにmu_errという「水準成分の増減量」があります。
transformed parametersブロックはいったん飛ばして、modelブロックを見ます。
mu_err[1]は、無情報事前分布を指定しました。これは、『Bayesian structural time series modeling』という、最初に挙げた参考資料と異なったやり方です。とはいえ、初期状態が0近辺にあるという保証はないので、ここは無情報事前分布を使うほうが自然かと思いました。ここはいろいろの実装があり得そうです。
mu_err[2]以降は、標準偏差1の正規乱数とみなしています。
観測方程式は、ベクトル化したバージョンのコードと同じです。
mu_errからmuを得るのがtransformed parametersブロックです。
1時点目のmuはmu_errと同じとしています。
2時点目以降が重要です。forループの中です。
標準偏差1の正規乱数すなわちmu_errに対して、過程誤差の標準偏差s_wを掛け合わせることで、実際の過程誤差としています。
このように「増減量を外だし」してあげることで、モデルの収束が良くなるようです。このような事例はGLMMなどの階層モデルでしばしばみられますね。
実行すると、ワーニングが減りました。しかし、adapt_deltaを変えるよう促されています。
> # 再パラメータ化 > mod_ll_remodeling <- stan( + file = "local-level-remodeling.stan", + data = data_list_1, + seed = 1 + ) Warning messages: 1: There were 8 divergent transitions after warmup. Increasing adapt_delta above 0.8 may help. See http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup 2: Examine the pairs() plot to diagnose sampling problems
ワーニングメッセージの通りに、adapt_deltaやmax_treedepthを増やして再実行させます。
すると、きれいにワーニングがなくなりました。
> # adapt_deltaを増やす > mod_ll_remodeling_2 <- stan( + file = "local-level-remodeling.stan", + data = data_list_1, + seed = 1, + control = list(adapt_delta = 0.9, max_treedepth = 15) + )
再パラメータ化したローカル線形トレンドモデル
最後に、ローカル線形トレンドモデルのStanコードを修正します。
『local-trend-remodeling.stan』という名称で保存しておきます。
data {
int T; // データ取得期間の長さ
vector[T] y; // 観測値
}
parameters {
real<lower=0> s_w; // 水準成分の変動の大きさを表す標準偏差
real<lower=0> s_z; // ドリフト成分の変動の大きさを表す標準偏差
real<lower=0> s_v; // 観測誤差の標準偏差
vector[T] mu_err; // 水準成分の増減量
vector[T] delta_err; // ドリフト成分の増減量
}
transformed parameters {
// transformed parametersで実際の状態を得る
vector[T] mu; // 水準+ドリフト成分の推定値
vector[T] delta; // ドリフト成分の推定値
// 1時点目
mu[1] = mu_err[1];
delta[1] = delta_err[1];
// 2時点目以降
for (t in 2:T) {
mu[t] = mu[t-1] + delta[t-1] + s_w * mu_err[t];
delta[t] = delta[t-1] + s_z * delta_err[t];
}
}
model {
// 標準偏差1の正規乱数を得る
mu_err[2:T] ~ normal(0,1);
delta_err[2:T] ~ normal(0,1);
// 観測方程式
y ~ normal(mu, s_v);
}
基本的な方針は、ローカルレベルモデルと同じです。
増減量をmu_errやdelta_errとして外だしします。また、これらを標準偏差1の正規分布だとみなし、これにs_wやs_zという標準偏差を表すパラメータを掛け合わせることで、実際の状態の推定値を得ています。
上記のコードを使って実行した結果はこちらです。
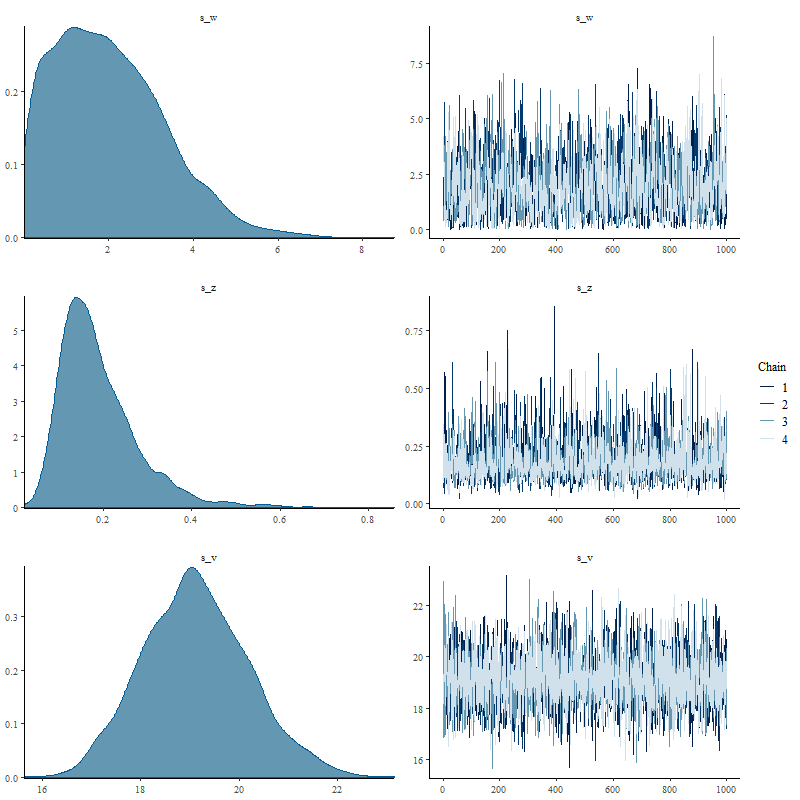
大きく改善されました。とはいえワーニングはまだ少し残っているようです。
> # 再パラメータ化 > mod_llt_remodeling <- stan( + file = "local-trend-remodeling.stan", + data = data_list_1, + seed = 1 + ) Warning messages: 1: There were 98 divergent transitions after warmup. Increasing adapt_delta above 0.8 may help. See http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup 2: Examine the pairs() plot to diagnose sampling problems
ワーニングに従い、adapt_deltaやmax_treedepthを増やすと、ワーニングは一切出ません。
> # adapt_deltaを増やす > # 再パラメータ化 > mod_llt_remodeling_2 <- stan( + file = "local-trend-remodeling.stan", + data = data_list_1, + seed = 1, + control = list(adapt_delta = 0.99, max_treedepth = 15) + )
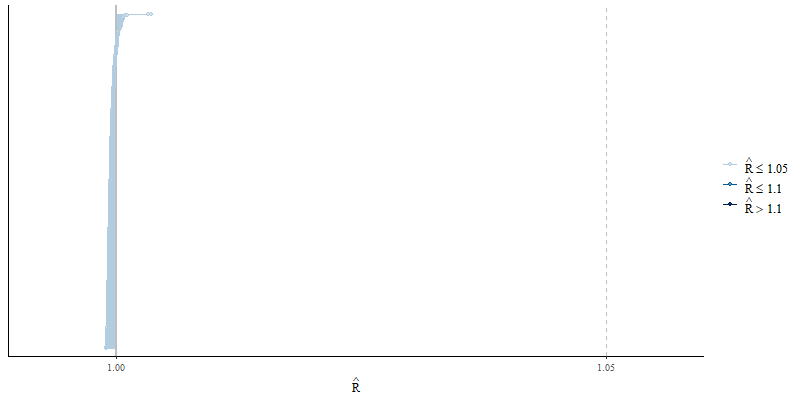
推定結果を確認すると、Rhatは1になっているようです。
> # 問題なし
> print(mod_llt_remodeling_2, pars = c("s_w", "s_z", "s_v"))
Inference for Stan model: local-trend-remodeling.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
s_w 2.01 0.04 1.31 0.12 0.99 1.86 2.85 4.92 1128 1
s_z 0.19 0.00 0.09 0.07 0.13 0.17 0.23 0.41 1986 1
s_v 19.13 0.02 1.08 17.12 18.38 19.10 19.84 21.37 4508 1
状態推定値も含めて、すべての推定値のRhatを確認しても、問題ないようです。
# 収束の確認 mcmc_rhat(rhat(mod_llt_remodeling_2))
トレースプロットなどを得ると、とてもきれいな形になりました。
# 事後分布の可視化
mcmc_combo(mod_llt_remodeling_2, pars = c("s_w", "s_z", "s_v"))
参考文献
|
RとStanではじめる ベイズ統計モデリングによるデータ分析入門 このブログの管理人が書いたベイズ統計モデリングの入門書です。 RとStanを使ってベイズ統計モデリングをするための基本をまとめています。初めてベイズ統計モデリングをやってみようという方にお勧めします。 本記事は、この書籍を補足する意味も持たせています。今後も、書籍をサポートする内容を充実させていきたいと思います。 サポートページはこちらです。 |
 |
|
StanとRでベイズ統計モデリング こちらはより応用的な内容が載っているベイズ統計モデリングの教科書です。Stanのコードも豊富にあります。 |
 |
書籍以外の参考文献
Bayesian structural time series modeling
スポンサードリンク
更新履歴
2019年12月14日:新規作成