機械学習による時系列予測
最終更新:2017年7月26日
機械学習法を用いた時系列データの予測方法について説明します。
R言語を使えば、機械学習も時系列データのデータ操作も簡単にできます。
両者を組み合わせて、時系列データへの予測モデルを作成してみました。
ソースコードはこちらに置いてあります。
スポンサードリンク
目次
- 解析の準備
- 機械学習とは
- 今回予測するデータ
- caretパッケージを使う準備
- Rによる機械学習
- 予測モデルの概要
- ハイパーパラメタのチューニング
- 機械学習による時系列予測
- 最適な次数を選ぶ
- 当てはめ精度の評価
- 将来の予測
1.解析の準備
機械学習とは
機械学習とは、次にどのようなデータが来るのかを、決まった手順を踏んで予測する技術、あるいは手法のことです。
機械学習の良いところは、予測のための「手順」を、過去のデータからほとんど自動で見つけられることです。
昔は人間が勘と経験そして度胸で予測を出していました。
もちろん、優秀な予測者が会社を辞めてしまえば、もう予測はできなくなります。
少しIT技術が発展したころには、エキスパートシステムなどといって「気温が高くて晴れていればビールが良く売れる」といったルールを人間が考えて、そのルールに従って予測を出していました。
しかし、このやり方だととても細かくルールを設定しなければなりませんし、ルールを設定し忘れてしまうと、変な予測結果が出てしまいます。
機械学習では、予測のためのルールを、文字通り「機械が学習」してくれます。
人間がいちいちルールを指定してやる必要はありません。
詳しくは『機械学習とは何か』を参照してください。
今回予測するデータ
機械学習といえば「気温を使ってビールの売上を予測する」といったように、色々なデータを組み合わせて予測した計算例が多いかと思います。
しかし、今回予測するデータは時系列データです。
今回は毎月の飛行機乗客数のデータを使います。
この場合「先月の乗客数が多ければ、来月も多くなるのではないか」といったように、過去から未来を予測していきます。
時間という情報を基にして将来を予測する方法を学んでください。
データはR言語に組み込みの『Airpassengers』を使います。
> # 原系列
> AirPassengers
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949 112 118 132 129 121 135 148 148 136 119 104 118
1950 115 126 141 135 125 149 170 170 158 133 114 140
1951 145 150 178 163 172 178 199 199 184 162 146 166
1952 171 180 193 181 183 218 230 242 209 191 172 194
1953 196 196 236 235 229 243 264 272 237 211 180 201
1954 204 188 235 227 234 264 302 293 259 229 203 229
1955 242 233 267 269 270 315 364 347 312 274 237 278
1956 284 277 317 313 318 374 413 405 355 306 271 306
1957 315 301 356 348 355 422 465 467 404 347 305 336
1958 340 318 362 348 363 435 491 505 404 359 310 337
1959 360 342 406 396 420 472 548 559 463 407 362 405
1960 417 391 419 461 472 535 622 606 508 461 390 432
しかし、このデータをそのまま使うのではなく、少し変換してから使います。
変換前のもともとのデータのことを原系列などと呼ぶことがあります。
原系列に対して、対数差分系列を作ります。
> ## 対数差分系列への適用
> log_diff_passenger <- diff(log(AirPassengers))
> log_diff_passenger
Jan Feb Mar Apr May Jun Jul
1949 0.052185753 0.112117298 -0.022989518 -0.064021859 0.109484233 0.091937495
1950 -0.025752496 0.091349779 0.112477983 -0.043485112 -0.076961041 0.175632569 0.131852131
1951 0.035091320 0.033901552 0.171148256 -0.088033349 0.053744276 0.034289073 0.111521274
1952 0.029675768 0.051293294 0.069733338 -0.064193158 0.010989122 0.175008910 0.053584246
1953 0.010256500 0.000000000 0.185717146 -0.004246291 -0.025863511 0.059339440 0.082887660
1954 0.014815086 -0.081678031 0.223143551 -0.034635497 0.030371098 0.120627988 0.134477914
1955 0.055215723 -0.037899273 0.136210205 0.007462721 0.003710579 0.154150680 0.144581229
1956 0.021353124 -0.024956732 0.134884268 -0.012698583 0.015848192 0.162204415 0.099191796
1957 0.028987537 -0.045462374 0.167820466 -0.022728251 0.019915310 0.172887525 0.097032092
1958 0.011834458 -0.066894235 0.129592829 -0.039441732 0.042200354 0.180943197 0.121098097
1959 0.066021101 -0.051293294 0.171542423 -0.024938948 0.058840500 0.116724274 0.149296301
1960 0.029199155 -0.064378662 0.069163360 0.095527123 0.023580943 0.125287761 0.150673346
Aug Sep Oct Nov Dec
1949 0.000000000 -0.084557388 -0.133531393 -0.134732594 0.126293725
1950 0.000000000 -0.073203404 -0.172245905 -0.154150680 0.205443974
1951 0.000000000 -0.078369067 -0.127339422 -0.103989714 0.128381167
1952 0.050858417 -0.146603474 -0.090060824 -0.104778951 0.120363682
1953 0.029852963 -0.137741925 -0.116202008 -0.158901283 0.110348057
1954 -0.030254408 -0.123344547 -0.123106058 -0.120516025 0.120516025
1955 -0.047829088 -0.106321592 -0.129875081 -0.145067965 0.159560973
1956 -0.019560526 -0.131769278 -0.148532688 -0.121466281 0.121466281
1957 0.004291852 -0.144914380 -0.152090098 -0.129013003 0.096799383
1958 0.028114301 -0.223143551 -0.118092489 -0.146750091 0.083510633
1959 0.019874186 -0.188422419 -0.128913869 -0.117168974 0.112242855
1960 -0.026060107 -0.176398538 -0.097083405 -0.167251304 0.102278849
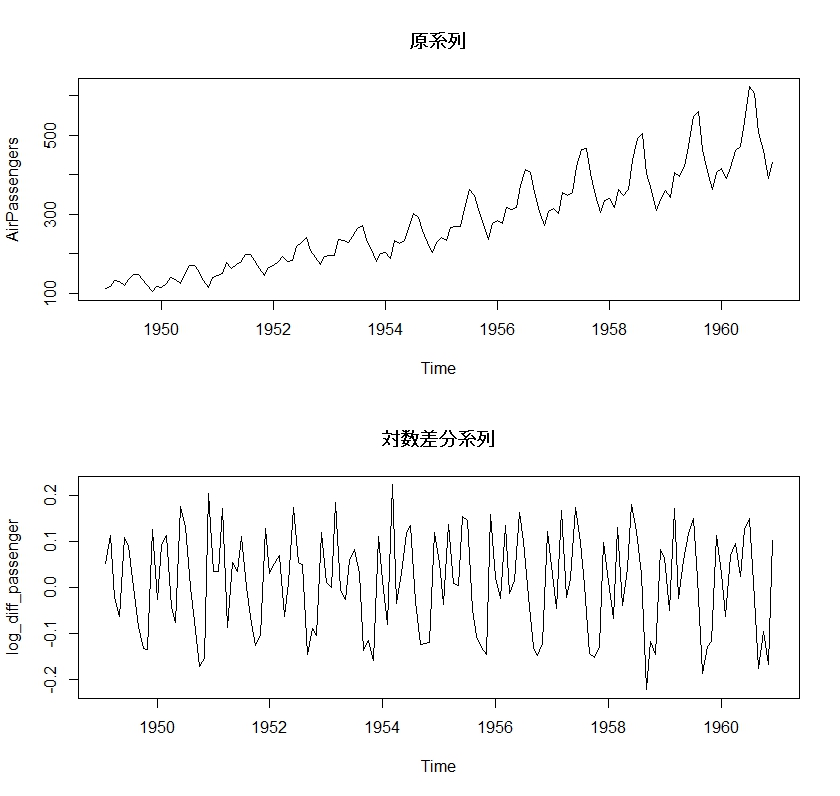
原系列と対数差分系列のグラフを描いておきます。
# 図示 par(mfrow=c(2,1)) plot(AirPassengers, main="原系列") plot(log_diff_passenger, main="対数差分系列") par(mfrow=c(1,1))
差分系列とは、例えば{4,7,5}というデータがあった時{7-4,5-7}={3,-2}というようにスライドして差をとった結果のことです。
あらかじめ対数をとることにより、データを計算しやすい幅に収めやすくなる、また、対数差分系列は近似的に「変化率」の推移と等しくなるので解釈がしやすくなるというメリットが得られます。
なお、差分をとった時に、最初のデータが(差分を計算できないので)無くなってしまうことに注意してください。
元に戻すには、差分系列の累積和を計算してから、「一番最初の値」を足してやればよいです。
先の例ですと、差分系列が{3,-2}でしたので、最初の値をいれて{4,3,-2}、累積和をとって{4,4+3,4+3-2}={4,7,5}に戻ります。
Rで確認してみます。
> # 元に戻す > exp(cumsum(log_diff_passenger) + log(AirPassengers[1])) [1] 118 132 129 121 135 148 148 136 119 104 118 115 126 141 135 125 149 170 170 158 133 114 140 [24] 145 150 178 163 172 178 199 199 184 162 146 166 171 180 193 181 183 218 230 242 209 191 172 [47] 194 196 196 236 235 229 243 264 272 237 211 180 201 204 188 235 227 234 264 302 293 259 229 [70] 203 229 242 233 267 269 270 315 364 347 312 274 237 278 284 277 317 313 318 374 413 405 355 [93] 306 271 306 315 301 356 348 355 422 465 467 404 347 305 336 340 318 362 348 363 435 491 505 [116] 404 359 310 337 360 342 406 396 420 472 548 559 463 407 362 405 417 391 419 461 472 535 622 [139] 606 508 461 390 432
対数差分系列なので、対数を元に戻すために『exp』が入っていることを除けば同じことです。
元に戻せることはわかったので、まずは計算がしやすい対数差分系列にのみ焦点を当てて解析をしていきます。
データをもう少し変換します。
今度はデータの中身は変えません。
機械学習法を適用しやすいように整形します。
## ラグをとって、過去のデータを説明変数にする
# embed関数による整形
lag_num <- 4
exp_val_sample <- as.data.frame(embed(log_diff_passenger, lag_num))
# 列名の変更
colnames(exp_val_sample)[1] <- "Y"
for(i in 2:lag_num){
colnames(exp_val_sample)[i] <- paste("Lag", i-1, sep="")
}
こんなデータになります。
> # 整形されたデータ
> head(exp_val_sample)
Y Lag1 Lag2 Lag3
1 -0.06402186 -0.02298952 0.11211730 0.05218575
2 0.10948423 -0.06402186 -0.02298952 0.11211730
3 0.09193750 0.10948423 -0.06402186 -0.02298952
4 0.00000000 0.09193750 0.10948423 -0.06402186
5 -0.08455739 0.00000000 0.09193750 0.10948423
6 -0.13353139 -0.08455739 0.00000000 0.09193750
以下のような形式に整形されます。
Y:当月データ
Lag1:前月データ
Lag2:2か月前データ
Lag3:3か月前データ
このように整形することで、「過去のデータを説明変数にして、将来を予測する」機械学習モデルを作りやすくなります。
caretパッケージを使う準備
最後に、機械学習法を適用するためのパッケージを使う準備をします。
詳しくは『Rによる機械学習:caretパッケージの使い方』を参照してください。
## caretによる学習モデル作成の準備
# install.packages("kernlab")
# install.packages("caret")
# install.packages("e1071")
library(caret)
library(kernlab)
# 並列化演算を行う
# install.packages("doParallel")
library(doParallel)
cl <- makePSOCKcluster(detectCores())
registerDoParallel(cl)
今回は、後ほどサポートベクトルマシンという機械学習法を適用するため、それに関連するパッケージも入れておきました。
2.Rによる機械学習
予測モデルの概要
今回はサポートベクトルマシン(SVM)という機械学習法を適用してみます。
このモデルの詳細は『サポートベクトルマシンの考え方』を参照してください。
ニューラルネットワークの場合の計算は『ニューラルネットワークの考え方』に載っています。
今回はSVMのみを対象とします。
なお、この記事で紹介するやり方は、caretパッケージを使う場合は、他の学習モデルにも応用できます。
ハイパーパラメタのチューニング
先ほど作った学習データに対して、モデルを当てはめてみます。
# モデルの推定
set.seed(0)
tuned_svm_sample <- train(
Y ~ .,
data=exp_val_sample,
method = "svmRadial",
tuneGrid = expand.grid(C=c(1:5), sigma=2^c(-1:1)),
preProcess = c('center', 'scale')
)
『caret』パッケージの『train』関数を使えば、モデルの作成が簡単にできます。
以下、簡単にコードの説明をします。
4行目:Y(直近のデータ)を、他のデータ(過去のデータ)すべてを使って予測します
5行目:学習データの指定
6行目:予測モデルの指定。ガウシアンカーネルを使ったSVMを使用します
7行目:ハイパーパラメタをどの範囲で動かすかの指定。本来はサポートベクトル回帰ですのでεもチューニングしたかったのですが、caretパッケージではできないようでしたので、コストパラメタCとガウシアンカーネルのパラメタsigmaのみをチューニングしています。
8行目:データをあらかじめ標準化してね、という指定
10秒ほどで計算が終わります。
ハイパーパラメタのチューニング結果はこちら。
> # チューニングされたモデル > tuned_svm_sample Support Vector Machines with Radial Basis Function Kernel 140 samples 3 predictor Pre-processing: centered (3), scaled (3) Resampling: Bootstrapped (25 reps) Summary of sample sizes: 140, 140, 140, 140, 140, 140, ... Resampling results across tuning parameters: C sigma RMSE Rsquared 1 0.5 0.07922218 0.4719402 1 1.0 0.07616361 0.5058111 1 2.0 0.07670153 0.4935778 2 0.5 0.07931617 0.4802538 2 1.0 0.07795633 0.4939667 2 2.0 0.07960270 0.4643388 3 0.5 0.07963109 0.4814751 3 1.0 0.07976465 0.4831468 3 2.0 0.08130037 0.4501501 4 0.5 0.08011397 0.4806553 4 1.0 0.08146011 0.4720266 4 2.0 0.08283482 0.4388014 5 0.5 0.08084313 0.4776399 5 1.0 0.08305617 0.4612183 5 2.0 0.08388670 0.4315185 RMSE was used to select the optimal model using the smallest value. The final values used for the model were sigma = 1 and C = 1.
本来はこの後、もう少し細かくハイパーパラメタのチューニングをしたほうが良いのですが、今回は省略します。
パラメタのチューニングに関しては、Yoshihiko Suhara様の以下のスライドなども参考にしてください。
素晴らしくよくまとまっています。
なお、caretパッケージを使うと、クロスバリデーションを用いた予測の評価とグリッドサーチによるパラメタのチューニング、データの標準化などを、train関数の内部でまとめて行うことができます。
最小の予測誤差、すなわち、最も良いパラメタを使った場合の予測誤差を見てみます。
『0.076』くらいとなりました。
> # 最小のRMSE(予測誤差) > tuned_svm_sample$results$RMSE [1] 0.07922218 0.07931617 0.07963109 0.08011397 0.08084313 0.07616361 0.07795633 0.07976465 [9] 0.08146011 0.08305617 0.07670153 0.07960270 0.08130037 0.08283482 0.08388670 > min(tuned_svm_sample$results$RMSE) [1] 0.07616361
最も予測誤差が小さくなるパラメタがいくらなのか見てみます。
> # チューニングされたハイパーパラメタ > tuned_svm_sample$bestTune sigma C 2 1 1
最後に、推定されたSVMの計算結果を取得します。
『サポートベクトルマシンの考え方』に載っていた様々な二次解析をしたいならば、この結果を使えばよいです。
> # SVMのモデルだけを取り出す > tuned_svm_sample$finalModel Support Vector Machine object of class "ksvm" SV type: eps-svr (regression) parameter : epsilon = 0.1 cost C = 1 Gaussian Radial Basis kernel function. Hyperparameter : sigma = 1 Number of Support Vectors : 112 Objective Function Value : -47.2828 Training error : 0.296877
スポンサードリンク
3.機械学習による時系列予測
最適な次数を選ぶ
モデルの作り方がわかったので、次は最適な次数を選ぶ方法を説明します。
次数とは、例えば「前月データだけを使って予測する」なら次数は1となります。
2か月前までのデータを使うなら次数は2です。
何か月前までのデータを使うと最も予測精度が高くなるのか。それをこれから調べるということです。
ここからはコードが長く続きます。
コピペしても動きますので、要所だけ理解していただければと思います。
まずは、予測精度や予測モデルを保管しておく入れ物を用意しておきます。
## 最適な次数を選ぶ # 予測精度などを格納する入れ物 sim_result <- data.frame( order=numeric(), error=numeric(), C=numeric(), sigma=numeric() ) # 予測モデルの一覧を格納する入れ物 tuned_models <- list()
次に、最大ラグ数を指定して、データを整形します。
今回は12を最大ラグ数としました。MAXで12か月前までのデータを使って予測するモデルを作るということです。
なお、直近のデータだけテスト用に残しておきました。
# 最大ラグ数
lag_max <- 12
# 訓練データの作成
# 最後のデータだけテスト用に残しておく
exp_val <- as.data.frame(embed(log_diff_passenger[-length(log_diff_passenger)], lag_max + 1))
colnames(exp_val)[1] <- "Y"
for(i in 2:(lag_max+1)){
colnames(exp_val)[i] <- paste("Lag", i-1, sep="")
}
Lag12まで作られました。
> # 訓練データ表示
> head(exp_val)
Y Lag1 Lag2 Lag3 Lag4 Lag5 Lag6 Lag7
1 0.09134978 -0.02575250 0.12629373 -0.13473259 -0.13353139 -0.08455739 0.00000000 0.09193750
2 0.11247798 0.09134978 -0.02575250 0.12629373 -0.13473259 -0.13353139 -0.08455739 0.00000000
3 -0.04348511 0.11247798 0.09134978 -0.02575250 0.12629373 -0.13473259 -0.13353139 -0.08455739
4 -0.07696104 -0.04348511 0.11247798 0.09134978 -0.02575250 0.12629373 -0.13473259 -0.13353139
5 0.17563257 -0.07696104 -0.04348511 0.11247798 0.09134978 -0.02575250 0.12629373 -0.13473259
6 0.13185213 0.17563257 -0.07696104 -0.04348511 0.11247798 0.09134978 -0.02575250 0.12629373
Lag8 Lag9 Lag10 Lag11 Lag12
1 0.10948423 -0.06402186 -0.02298952 0.11211730 0.05218575
2 0.09193750 0.10948423 -0.06402186 -0.02298952 0.11211730
3 0.00000000 0.09193750 0.10948423 -0.06402186 -0.02298952
4 -0.08455739 0.00000000 0.09193750 0.10948423 -0.06402186
5 -0.13353139 -0.08455739 0.00000000 0.09193750 0.10948423
6 -0.13473259 -0.13353139 -0.08455739 0.00000000 0.09193750
最後に、次数を変えながら計算を繰り返し、その都度予測モデルと予測精度を保存しておきます。
計算には若干の時間がかかることに注意してください。
時間がかかるため、パラメタのチューニングはかなり荒くしてあります。
# ループさせて、最も予測精度が高くなるラグ数を調べる
set.seed(0)
for(i in 1:lag_max) {
# 必要なラグまで、データを切り落とす
exp_val_tmp <- exp_val[,c(1:(i+1))]
# 予測モデルの作成
tuned_svm <- train(
Y ~ .,
data=exp_val_tmp,
method = "svmRadial",
tuneGrid = expand.grid(C=c(1:3), sigma=2^c(-1:1)),
preProcess = c('center', 'scale')
)
# 予測モデルを保存する
tuned_models <- c(tuned_models, list(tuned_svm))
# 予測精度などを保存する
sim_result[i, "order"] <- i
sim_result[i, "error"] <- min(tuned_svm$results$RMSE)
sim_result[i, "sigma"] <- tuned_svm$bestTune["sigma"]
sim_result[i, "C"] <- tuned_svm$bestTune["C"]
}
次数と予測精度の関係を図示してみました。
# ラグと予測精度の関係 plot( sim_result$error ~ sim_result$order, main="次数と予測誤差の関係", xlab="order", ylab="error" )
次数は8がちょうどよいようです。
予測誤差はクロスバリデーション法を使って計算されています。そのため、次数を増やしすぎて過学習を起こしてしまったかどうかを確認することもできます。
次数が9以上になると、予測誤差が増えていることがわかります。
当てはめ精度の評価
次に、予測精度や最も予測精度の高かったモデルを取り出します。
> # 最も予測精度が高かったモデルの評価結果 > subset(sim_result, sim_result$error==min(sim_result$error)) order error C sigma 8 8 0.0535919 3 0.5 > > # 次数だけを取り出す > best_order <- subset(sim_result, sim_result$error==min(sim_result$error))$order > best_order [1] 8 > > ## 当てはまりの精度の確認 > # 最も予測精度が高かったモデルを取り出す > best_model <- tuned_models[[best_order]] > best_model Support Vector Machines with Radial Basis Function Kernel 130 samples 8 predictor Pre-processing: centered (8), scaled (8) Resampling: Bootstrapped (25 reps) Summary of sample sizes: 130, 130, 130, 130, 130, 130, ... Resampling results across tuning parameters: C sigma RMSE Rsquared 1 0.5 0.05391555 0.7640257 1 1.0 0.06651616 0.6642469 1 2.0 0.08317458 0.4946397 2 0.5 0.05365691 0.7641736 2 1.0 0.06603826 0.6655936 2 2.0 0.08265172 0.4959744 3 0.5 0.05359190 0.7651059 3 1.0 0.06603801 0.6655976 3 2.0 0.08265171 0.4959739 RMSE was used to select the optimal model using the smallest value. The final values used for the model were sigma = 0.5 and C = 3.
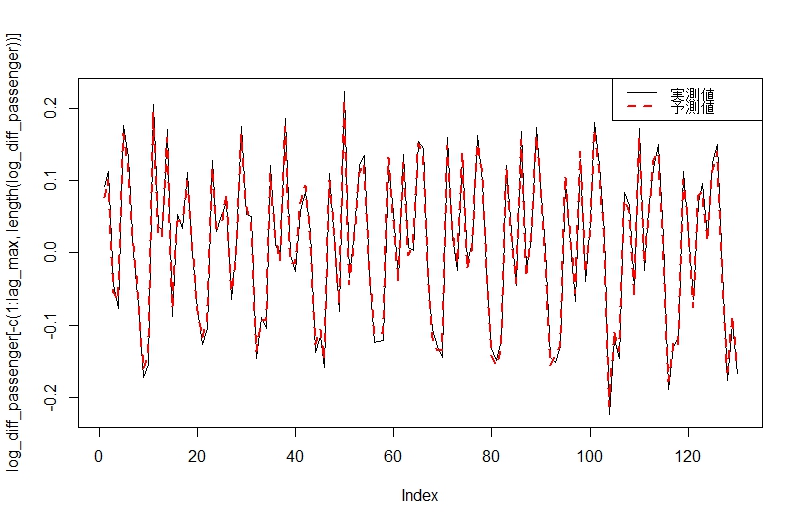
予測値と実測値のプロットを描いてみます。
なお、これは「手持ちのデータへの当てはまり」の精度であることに注意してください。
# 予測値と実測値のプロット
plot(log_diff_passenger[-c(1:lag_max, length(log_diff_passenger))], type="l")
lines(predict(best_model), col=2, lwd=2, lty=2)
legend(
legend=c("実測値", "予測値"),
"topright",
col=c(1,2),
lwd=c(1,2),
lty=c(1,2)
)
将来の予測
最後に1期先の予測を出してみます。
予測そのものは『predict』関数を使えばすぐにできるのですが、説明変数を作るのが若干面倒です。
以下のように、データをスライドさせることで、予測のための説明変数を作りました。
> # 説明変数を作る
> # 直近のデータだけを抽出
> last_data <- exp_val[nrow(exp_val), 1:best_order]
>
> # 列名を、学習データに合わせる
> for(i in 1:best_order){
+ colnames(last_data)[i] <- paste("Lag", i, sep="")
+ }
>
> # 説明変数を表示
> last_data
Lag1 Lag2 Lag3 Lag4 Lag5 Lag6 Lag7 Lag8
130 -0.1672513 -0.0970834 -0.1763985 -0.02606011 0.1506733 0.1252878 0.02358094 0.09552712
予測結果はこちらです。
> # 1期先の予測 > predict(best_model, last_data) [1] 0.07098058 > > # 正解データと比較 > log_diff_passenger[length(log_diff_passenger)] [1] 0.1022788
若干ずれていますが、直近のデータが『-0.1672513』であったため、それよりかは増えるというところは予測できていました。
機械学習法は「予測が当たりさえすればよい」という発想で作られているところもあるので、データからの知識発見にはあまり向いていませんが、予測精度は良い印象があります。
時系列データに対して簡単に実行ができるというのであれば、ARIMAモデルなどの標準的な手法と並行して使うことも検討してよいのではないかと思います。
参考文献
|
サポートベクトルマシン (機械学習プロフェッショナルシリーズ) この一冊を読めば、サポートベクトルマシンのことは大体わかります。 いま、サポートベクトルマシンの勉強をしたいと思ったら、この本から始めるのが良いと思います。 |
 |
|
はじめてのパターン認識 様々な機械学習法が載った書籍です。 どのテーマも簡潔にまとまっている、この分野では有名な書籍です。 |
 |
スポンサードリンク



いつも有用な情報ありがとうございます。
時系列データのリサンプリング手法について教えてほしいです。
SVMの最適次数を探索するときに、リサンプリングしたデータを使っても良いのでしょうか?
(時系列データをリサンプリングするのはOKなんでしょうか?)
感覚的に時系列データをリサンプリングすると、時間のつながりが失われるような気がしています。
タカハシ様
コメントありがとうございます。
管理人の馬場です。
ご指摘の通りで、時系列分析をする場合には、
通常のリサンプリングが奨励されないことがあります。
下記の記事のように、時系列データのためのクロスバリデーション法を使う方法もあります。
https://logics-of-blue.com/time-series-forecast-and-evaluation-with-cv/
ただ、今回のモデルは純粋な自己回帰のモデルとなっています。
自己回帰モデルで表現できる構造であり、正しいモデルがネストされている場合には、
通常のK-fold CVを使っても支障ないことが、シミュレーションや実データへの適用事例から示唆されています。
(ただし、いくつかの仮定を満たす必要があります)
https://robjhyndman.com/papers/cv-wp.pdf
ただし、残差に自己相関が残っている場合には、
通常のK-fold CVは非推奨となります。
なので本来は一度Box検定などを実行して、残差の自己相関の評価などを行った方が良いのでしょうね。
今回は季節性のあるデータなので、もう少し探索すべき次数の範囲を増やすべきだったかもしれません。
この辺りのベストプラクティスはなかなか見当たらないので、
正直、当方も手探りなところが一部あります。
馬場様
時系列データのリサンプリングについてのご説明ありがとうございます。
リンク先を見ながら勉強したいと思います。
コメント後に思ったんですが、機械学習と時系列予測がごっちゃになって
時間が連続したデータが必要と思い込んでいました。
サイトや書籍の説明が分かりやすくて、いつも助かっています。
ご活躍をお祈りいたします。