サポートベクトルマシンの考え方
予測には過去のデータを使います。しかし、外れ値のような余計なデータまで使ってしまうと、予測精度が下がるかもしれません。
そこで「本当に予測に必要となる一部のデータ」だけを使います。
「本当に予測に必要となる一部のデータ」のことをサポートベクトルと呼び、サポートベクトルを用いた機械学習法がサポートベクトルマシン(Sapport vector machine:SVM)です。
ここでは、分類・回帰に分けたサポートベクトルマシンの概要と、R言語を用いた実装方法について説明します。
ソースコードはこちらに置いてあります。
スポンサードリンク
目次
- サポートベクトル分類の考え方
- マージン最大化とサポートベクトル
- ハードマージンとソフトマージン
- Rによる計算例:線形データ
- 非線形データへの対応とカーネル関数
- Rによる計算例:非線形データ
- 補足:パラメタ推定の工夫とカーネルトリック
- サポートベクトル回帰の考え方
- 回帰問題と分類問題
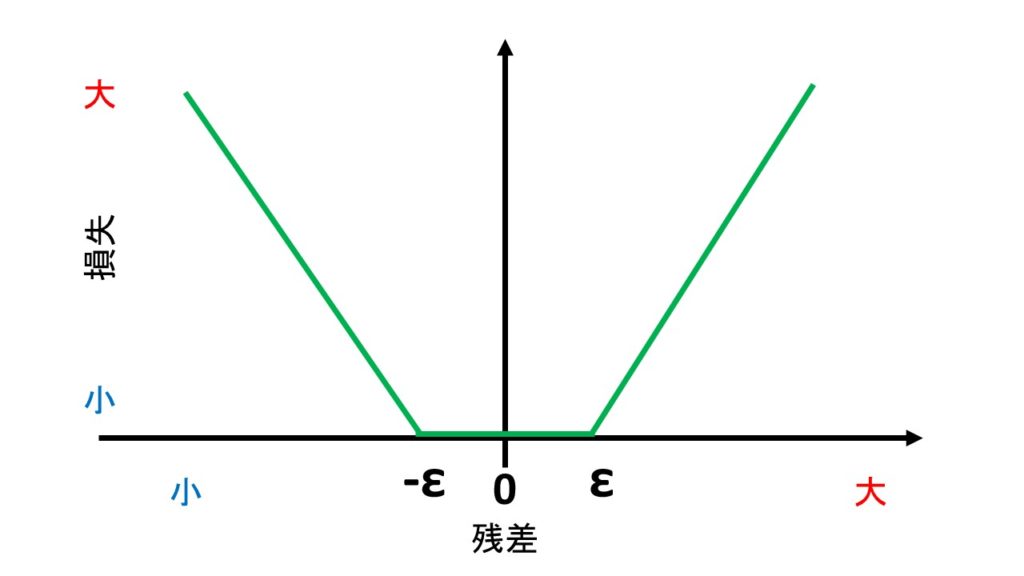
- ε-不感損失関数
- Rによる計算例:サポートベクトル回帰
- ハイパーパラメタのチューニング
1.サポートベクトル分類の考え方
マージン最大化とサポートベクトル
サポートベクトルマシンを理解するためには、名前の由来である「サポートベクトル」について理解する必要があります。
サポートベクトルとは、先に説明したように「予測に必要となる一部のデータ」です。
では「予測に必要となる一部のデータ」はどのようにして決められるのでしょうか。
それを定めるのに「マージン最大化」と呼ばれる考え方を使います。
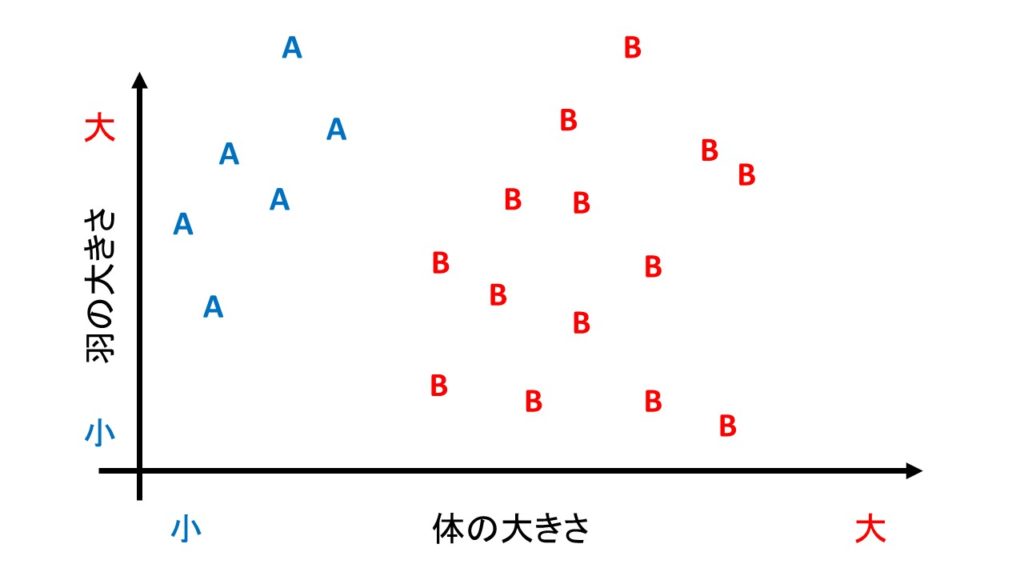
架空の鳥の種類を分類する問題を考えてみます。
体の特徴というデータを使って、鳥の種類を分類するサポートベクトルマシンを作ってみましょう。
下のグラフは
縦軸は「羽の大きさ」
横軸は「体の大きさ」
を現しています。
こいつらをどのように分類するかを考えます。
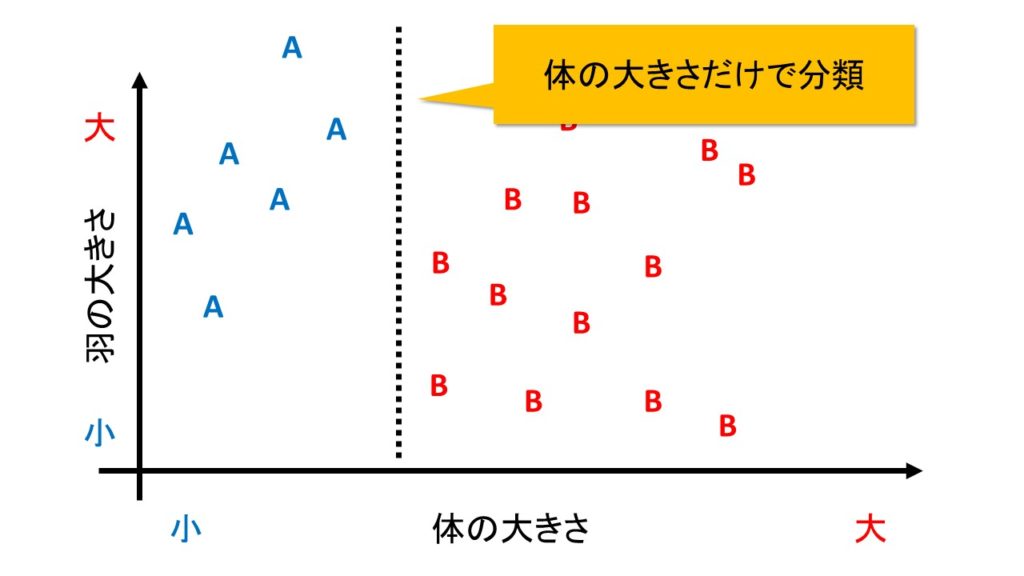
下の図は、体の大きさだけで分類してみたものです。
体が小さければA種、大きければB種と判定されることになります。
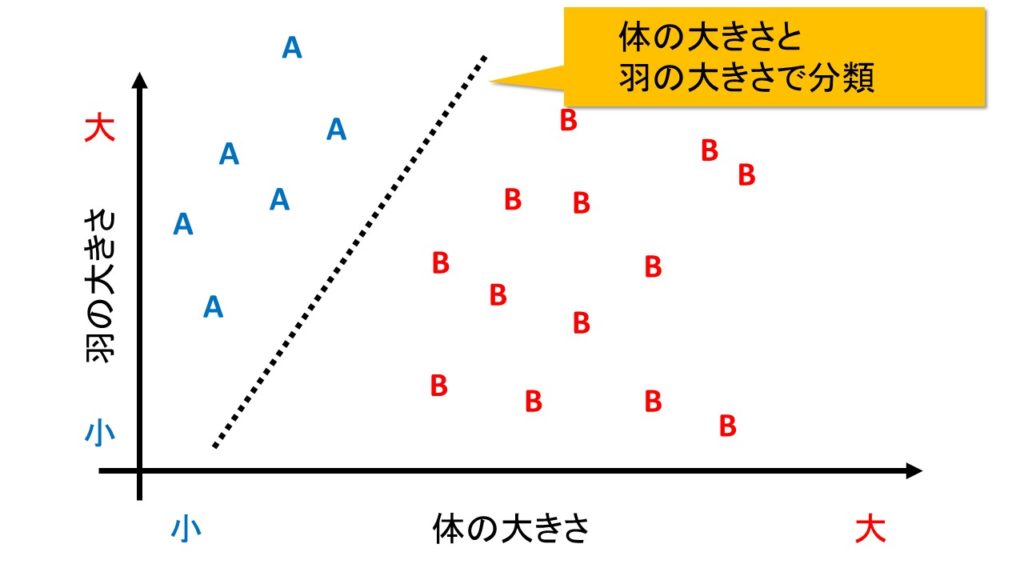
次の図は、体の大きさと、羽の大きさの両方を加味して分類してみたものです。
体が小さいわりに羽が大きければA種。体のわりに羽が小さければB種となります。
どちらのほうがよい分け方でしょうか。
これは「次に新しいデータが手に入ったとき、正しく分類できるかどうか」という基準で「よい」か「悪い」かを判別します。
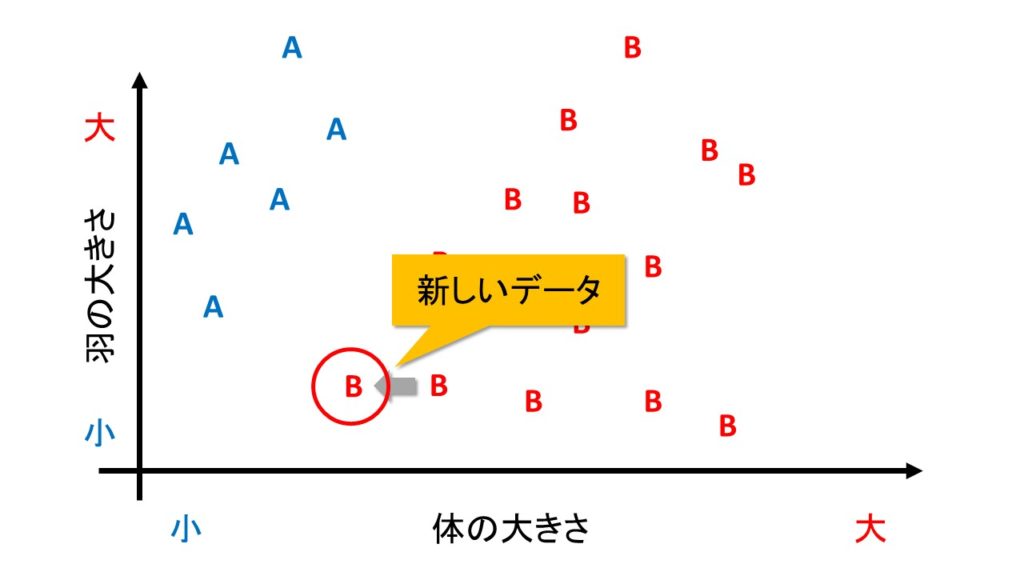
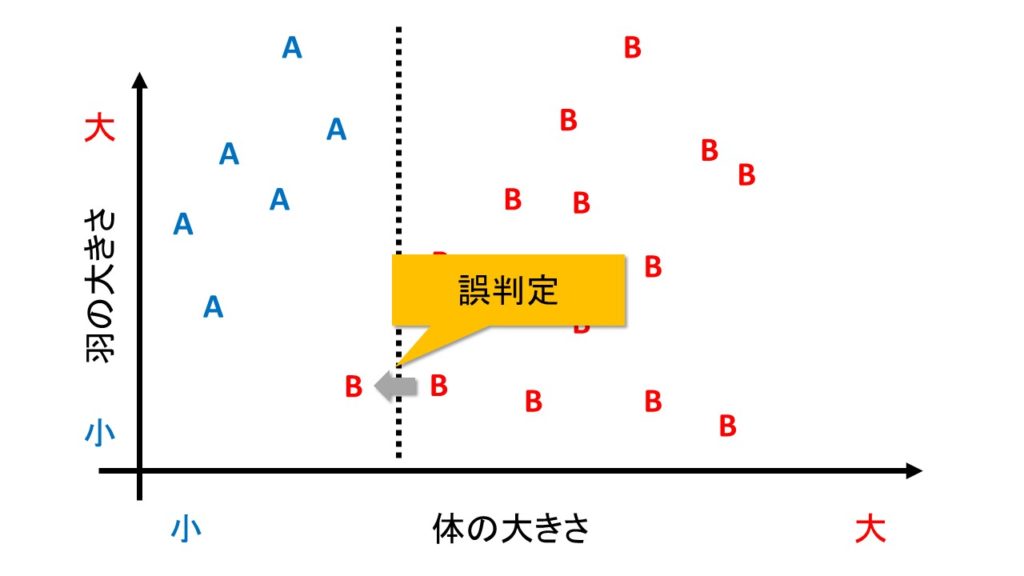
例えば、下の図のように、B種のデータが追加で入ったとします。
見た感じ、新しいデータも、B種のほかのデータととても近い位置にプロットされています。
しかし、1番目の分け方「体の大きさだけで分類」では、下の図のように、誤判別してしまいます。
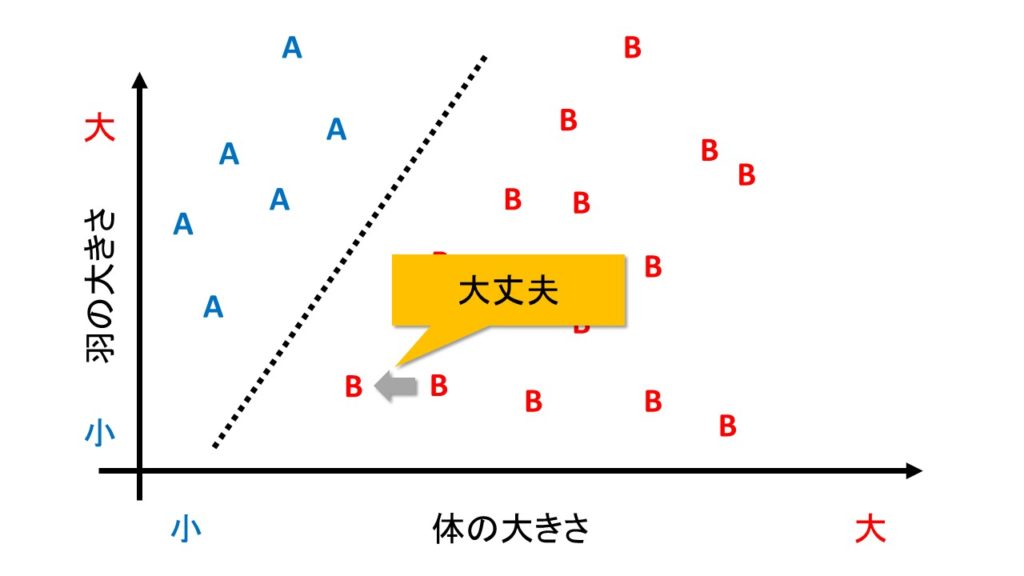
一方、2つ目の分け方「体の大きさと羽の大きさで分類」では、下の図のように、正しく分類します。
SVMでは、正しい分類基準を見つけるために、「マージン最大化」という考えを使います。
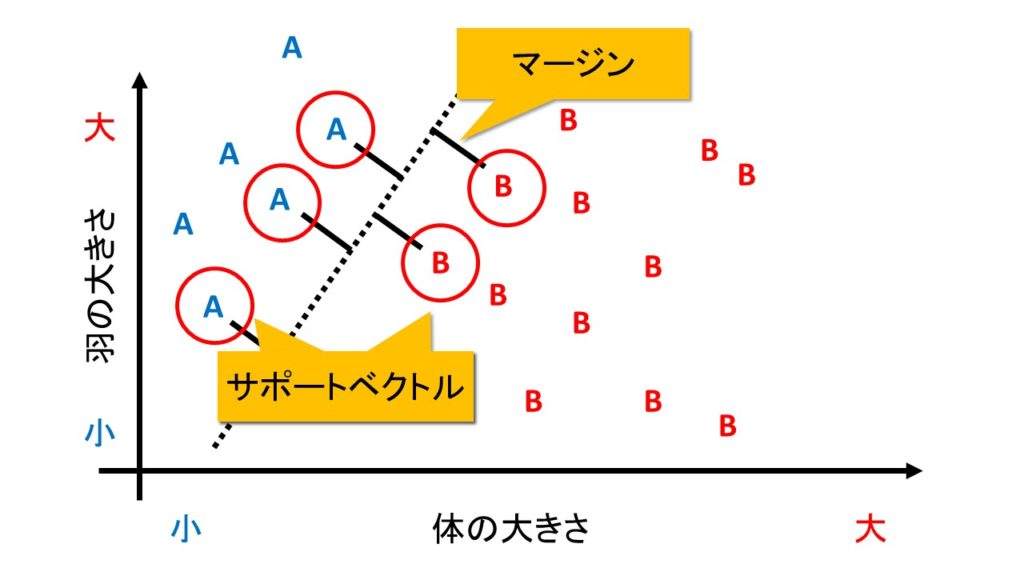
マージンとは、「判別する境界とデータとの距離」を指します。
これが大きければ、「ほんの少しデータが変わっただけで誤判定してしまう」というミスをなくすことができます。
なお、境界線と最も近くにあるデータを「サポートベクトル」と呼びます。
境界の近くにあるデータは、言い換えると「A種かB種か微妙」な位置にあるデータだとみなせます。
そんな「どっちか分けにくいやつら」が多いと困りますね。
なので、境界とデータとの距離、すなわちマージンを大きくするようにして誤判別を防ぐのです。
逆にいれば、誤判別を防ぐには「境界の近くにあるデータ」だけあれば十分です。
明らかに、ハッキリと分かれる奴らをいちいち考える必要はありません。
なので、境界の近くにあるデータ、すなわちサポートベクトルのみを用いて分類を行います。
サポートベクトル以外のデータの値が多少変化したとしても、分類のための境界線の位置は一切変わりません。
ハードマージンとソフトマージン
先ほどの例のようにA種かB種かはっきり分かれることを前提としたマージンを「ハードマージン」と呼びます。
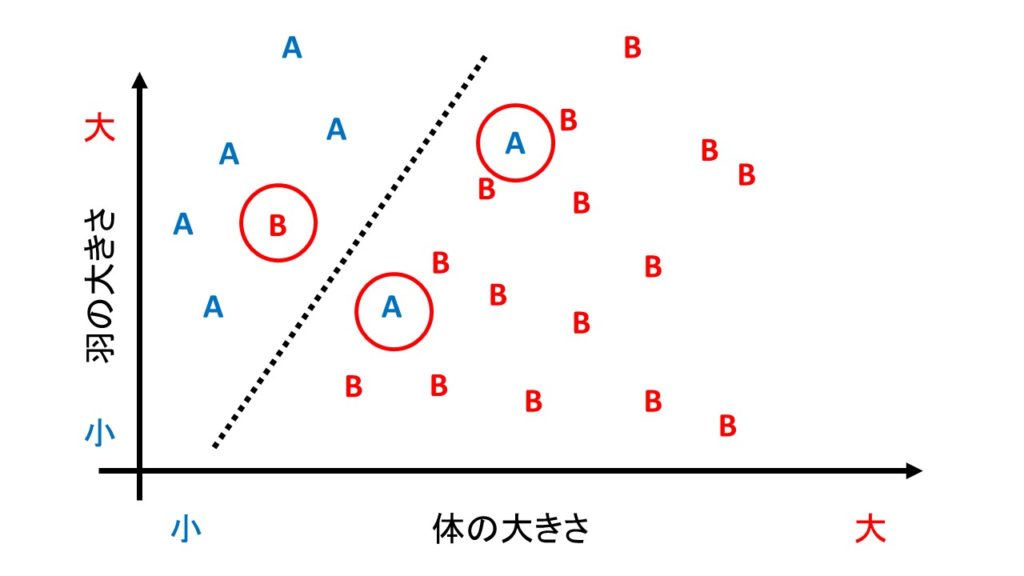
一方で、下の図のようにどうしても誤判別をしてしまうデータもあり得ます。
そういうデータに対して無理やり「100%正確な判別」をしてしまうと「体のわりに羽が大きければA種」という貴重な知見を見失ってしまいます。
すると、正しい分類規則を見失ってしまい、予測の精度が逆に下がってしまうこともあります。
「手持ちのデータ」に対して無理に適合性を高めてしまい、「まだ手に入れていないデータ」への予測精度が下がってしまう問題を「過学習」と呼びます。
過学習をせずに予測ができることを「汎化性」と呼び、この汎化性能を高めるために、あえて誤分類を許すように工夫します。
誤判別を許すことを前提としたマージンのことを「ソフトマージン」と呼びます。
ソフトマージン君は以下の2つを満たすように頑張ります。
・境界線とデータとはなるべく離れていたほうがいい
・誤判別はなるべく少ないほうがいい
そこで、以下の値を最小にするようにします。
$$\min \{ \frac{1}{マージン(サポートベクトルと境界線の距離)} + C \times{誤判別数} \}$$
パラメタ「C」という怪しげなのが出てきました。
これは「誤判別をどこまで許容するか」を現すパラメタです。
パラメタCが大きければ、誤判別は決して許さないし、逆にCが小さければ、誤判別はあまり気にしません。
パラメタCが∞に大きかった場合は「誤判別は1回も許さない」という強い制約となり、実質ハードマージンと変わらなくなります。
パラメタCが小さければ、多少誤判別があっても上記の式の合計は大きくならないので「誤判別を許しやすくなる」わけです。
パラメタCは人間があらかじめ決めてやる必要があります。
このように「あらかじめ与えられていることが前提のパラメタ」のことを「ハイパーパラメタ」などと呼びます。
パラメタCはとりあえずテキトーに決めるしかありませんが、グリッドサーチなどを使って「最も予測精度が高くなるようにパラメタをチューニングする」技術もあります。
これは後ほど解説します。
なお、ソフトマージンの場合は、誤判別されたデータに関しても「識別境界線を決める要素」すなわちサポートベクトルだとみなします。
Rによる計算例:線形データ
サポートベクトルマシンの計算例を見ていただくため、R言語で実装してみます。
ソースコードはこちらに置いてあります。
今回は『kernlab』という外部パッケージを使います。
必要なら『install.packages(“kernlab”)』としてインストールしてください。
『library(kernlab)』とすれば準備完了です。
まずは、サンプルデータを作って図示をしてみます。
先ほどの例と同じように、体と翼の大きさを使って、鳥の種類を分類してみます(架空のデータです)。
# サンプルデータ
bird <- data.frame(
wing = c(12, 10, 13, 10, 13, 12),
body = c(15, 20, 23, 30, 36, 39),
type = c("A","A", "A", "B", "B", "B")
)
# 図示
plot(
wing ~ body,
data=bird,
type="n",
main="鳥の羽と体の大きさ"
)
text(
wing ~ body,
data=bird,
rownames(bird),
col=c(1,2)[bird$type],
cex=2
)
『type=”n”』としてplot関数を使うと、軸だけを描いて、中身を空にできます。
そのうえで、text関数を使って、データの行番号をグラフに書き込みました。
数字は「何番目のデータか」を表した行番号です。
色は、種類AとBで分けてあります。黒が種類Aで、赤色が種類Bです。
このデータに対して、サポートベクトルマシンを適用してみます。
『ksvm』関数を使います。
# 線形のSV分類 svm_bird <- ksvm( type ~ wing + body, data=bird, type="C-svc", kernel="vanilladot" )
上記のコードの説明をします。
3行目:モデル式の指定です。「~」の左側に分類対象(今回は鳥の種類)を入れて、分類に使う説明変数を右側に入れます。
4行目:使うデータの指定
5行目:サポートベクトルマシンの分類の指定
サポートベクトルマシンといっても色々な種類があります。
分類と回帰でも種類が変わります。
今回は一番シンプルな分類をするように指定しました。
6行目:カーネル関数の指定です。後ほど解説します。
線形データへ適用させる場合は『vanilladot』を指定します。
結果はこちら。
> # 結果 > svm_bird Support Vector Machine object of class "ksvm" SV type: C-svc (classification) parameter : cost C = 1 Linear (vanilla) kernel function. Number of Support Vectors : 4 Objective Function Value : -1.5318 Training error : 0
『parameter : cost C = 1 』とあることから、パラメタCは(勝手に)1が設定されていることがわかります。
もちろん自分で設定することも可能です。
他に注意すべき点は、最終行の『Training error : 0 』です。誤判別が1つもなかったことがわかります。
10行目に『Number of Support Vectors : 4 』とあります。
サポートベクトル、すなわち「分類に使われたデータ数」は4つだけということがわかります。
何番目のデータが該当するのかは、『SVindex』という関数を使えばわかります。
> # サポートベクトル > SVindex(svm_bird) [1] 2 3 4 5
2,3,4,5番目のデータだけがサポートベクトルとなりました。
逆に言えば1,6番目のデータは、あってもなくても分類境界の作成に関与していないということがわかります。
これは図を見れはよくわかります。
サンプルデータの図を再掲します。

1,6番目は遠くに離れていますね。
こんな「見ればすぐにわかる」ような奴らはどうでもいいので、分類境界の作成に使われません。
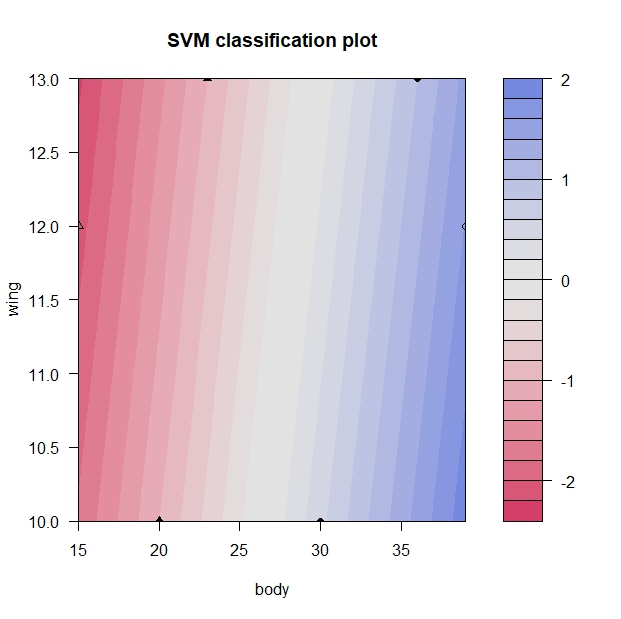
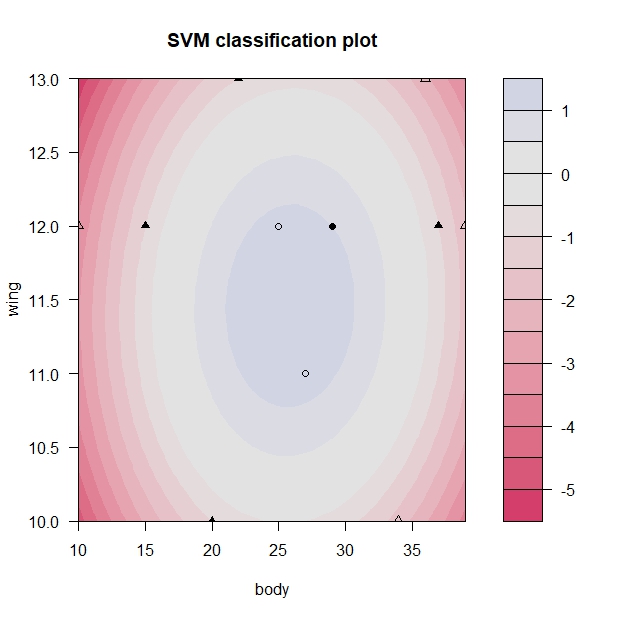
分類境界は『plot』関数を使えば図示できます。
# 分類境界の図示 plot(svm_bird, data=bird)
青色がプラスで赤色がマイナスです。正負の符合が切り替わる0の部分(白色)が境界線となります。
ちゃんと、少し斜めに線が引かれていることに注目してください。
マージン最大化のご利益です。
非線形データへの対応とカーネル関数
先ほどはまっすぐな線を引くだけで分類ができたのですが、いつもうまくいくとは限りません。
うまくいかないデータを作ってみました。
bird_2 <- data.frame(
wing = c(12, 12, 10, 13, 10, 13, 12, 12, 12, 12, 11),
body = c(10, 15, 20, 22, 34, 36, 39, 37, 25, 29, 27),
type = c("A", "A", "A", "A", "A", "A","A", "A", "B", "B", "B")
)
# 図示
plot(
wing ~ body,
data=bird_2,
type="n",
main="鳥の羽と体の大きさ(非線形)"
)
text(
wing ~ body,
data=bird_2,
rownames(bird_2),
col=c(1,2)[bird_2$type],
cex=2
)
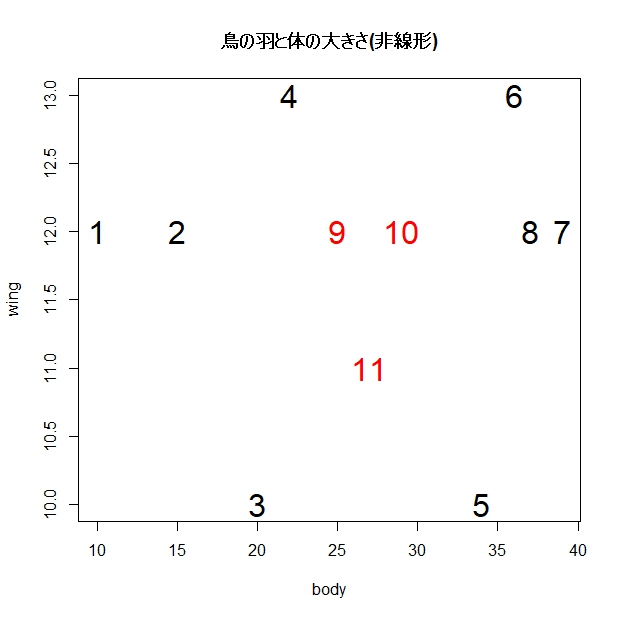
同じく、データの行番号をプロットしてみます。
色は鳥の種類ごとに分けてあります。
このグラフを見ると、分類のためには曲がった(非線形な)境界線を引かなければいけないことが予想できます。
また、1番と7番のデータは、分類境界の作成には役に立たなそうだ(サポートベクトルではない)ということも想像できますね。
このデータに対して、先ほどと同じように、線形のサポートベクトルマシンを適用してみます。
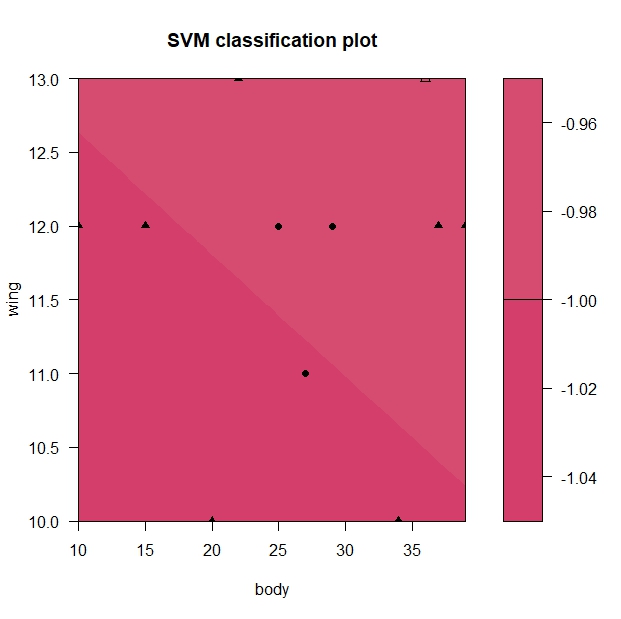
# 線形のSV分類。これだとうまくいかない svm_bird_dame <- ksvm( type ~ wing + body, data=bird_2, type="C-svc", kernel="vanilladot", C=25 ) # 分類境界の図示 plot(svm_bird_dame, data=bird_2)
結果はこちら。うまく分かれていません。
全部が赤色になっていることから想像ができますが、すべてのデータが種類Aであると分類されてしまいました。
> fitted(svm_bird_dame) [1] A A A A A A A A A A A Levels: A B
非線形なデータに対しては、データを変換してから分類境界を作るというのがサポートベクトルマシンで使われている方法です。
実際の計算とは異なるのですが、イメージをつかんでいただくために、以下の計算をしてみます。
新しい説明変数 = (羽の大きさ + 体の大きさ -39)2
Rで計算してみます。
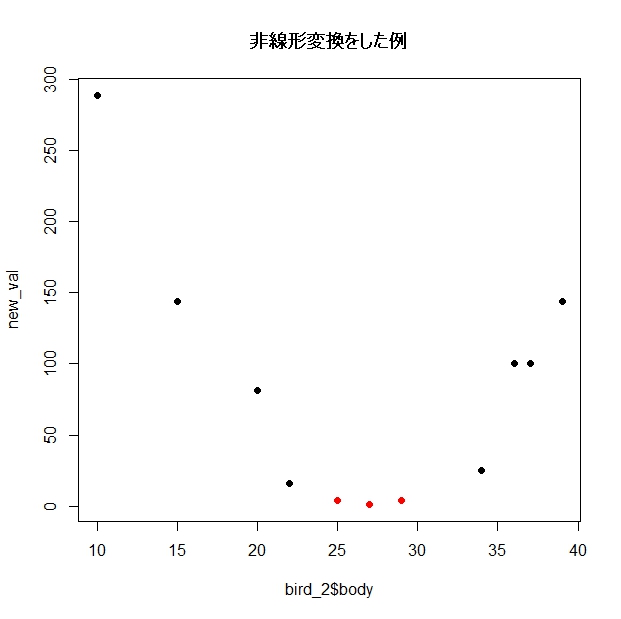
## 非線形にも対応するイメージ # 非線形変換の考え方 # (あくまで参考。SVMの実際の計算とは異なります) new_val <- (bird_2$wing + bird_2$body -39)^2 # 2乗した結果を新たに変数として使えば、分類できそう plot( new_val ~ bird_2$body, col=c(1,2)[bird_2$type], pch=16, main="非線形変換をした例" )
図示してみます。
赤色と黒色が分かれましたね。
先ほどの変換をして作った『new_val』が大きければA種、小さければB種とみなすことができそうです。
このようにデータをいったん変形してから分類をするという技術を使えば、非線形なデータにも対応が可能です。
なお、この変換の詳細は『補足:パラメタ推定の工夫とカーネルトリック』で解説します。
Rによる計算例:非線形データ
Rで非線形なデータへのサポートベクトル分類を試みます。
まずは多項式カーネルという変換を間に挟んでから分類してみます。
# 非線形のSV分類 # polydot(多項式カーネル) svm_bird_2 <- ksvm( type ~ wing + body, data=bird_2, type="C-svc", kernel="polydot", kpar = list(degree=2), C=25 )
多項式カーネルを使う場合は『kernel=”polydot”』と指定します。『kpar = list(degree=2)』とすると2乗の多項式を使うことができます。
またパラメタCは25にしておきました。
結果はこちら。
> # 結果 > svm_bird_2 Support Vector Machine object of class "ksvm" SV type: C-svc (classification) parameter : cost C = 25 Polynomial kernel function. Hyperparameters : degree = 2 scale = 1 offset = 1 Number of Support Vectors : 5 Objective Function Value : -1.7379 Training error : 0
『Training error : 0 』ですので、ちゃんと分類できたようです。
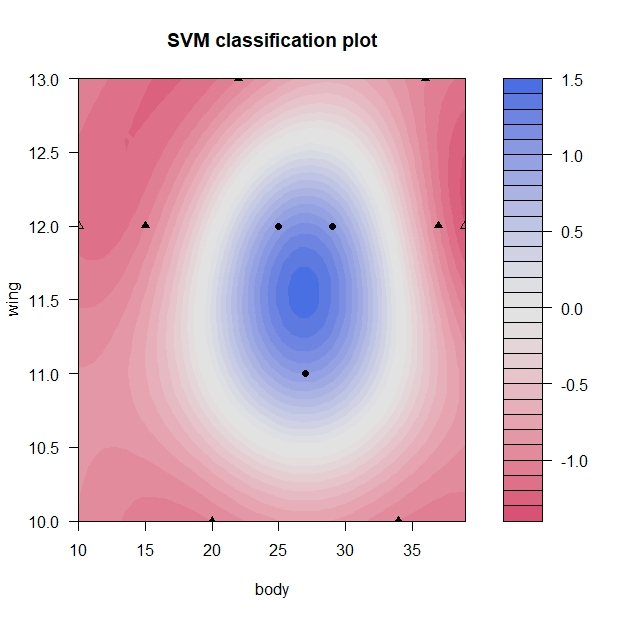
境界線を図示してみます。
# 分類境界の図示 plot(svm_bird_2, data=bird_2)
ちゃんと円形に分類境界線が引かれています。
次は、最もよく使われる変換である「ガウシアンカーネル」を使ってみます。
# 非線形のSV分類 # rbfdot(ガウシアンカーネル) svm_bird_3 <- ksvm( type ~ wing + body, data=bird_2, type="C-svc", kernel="rbfdot", kpar = list(sigma=1), C=25 )
『kernel=”rbfdot”』と指定します。
ガウシアンカーネルは、ちょっと難しいのですが、以下の式が使われています。
$$k(x, x’) = \exp( -\sigma\| x – x’\|^2 ) $$
後ほど計算例をお目にかけますが、sigmaが大きければ大きいほど、より「グネグネした」複雑な境界線が引かれる傾向があります。
すなわち手持ちのデータへはよく適合しますが、汎化性能が下がり、過学習しやすくなります。
先ほどのパラメタで実行した結果はこちらです。
> # 結果 > svm_bird_3 Support Vector Machine object of class "ksvm" SV type: C-svc (classification) parameter : cost C = 25 Gaussian Radial Basis kernel function. Hyperparameter : sigma = 1 Number of Support Vectors : 9 Objective Function Value : -3.577 Training error : 0 > > # サポートベクトル > SVindex(svm_bird_3) [1] 2 3 4 5 6 8 9 10 11
『Training error : 0 』なので、すべて正しく分類ができました。
また『SVindex』の結果から、サポートベクトルを見ると、やはり端っこの1番と7番のデータはサポートベクトルではないことがわかります。
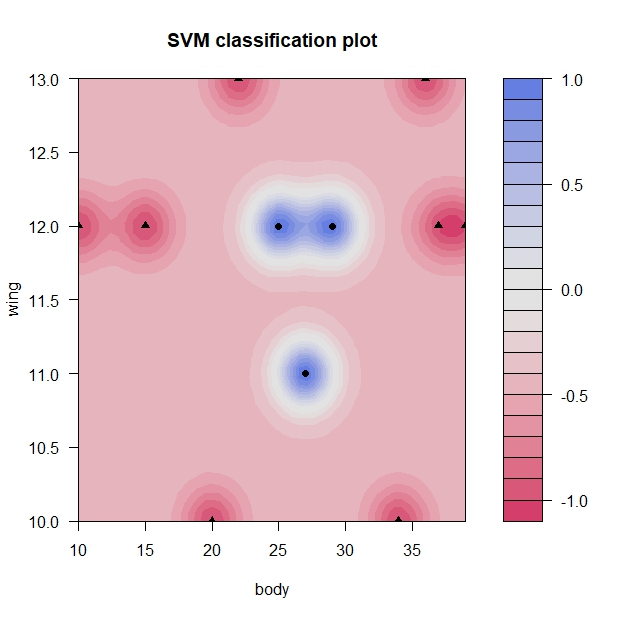
境界線を図示してみます。
# 分類境界の図示 plot(svm_bird_3, data=bird_2)
きれいな識別境界線が引けました。
次は、参考までに、sigmaを20にまで増やしてみます。
# 非線形のSV分類 # rbfdot(ガウシアンカーネル) # sigmaを増やした svm_bird_4 <- ksvm( type ~ wing + body, data=bird_2, type="C-svc", kernel="rbfdot", kpar = list(sigma=20), C=25 ) # 分類境界の図示 plot(svm_bird_4, data=bird_2)
分類境界線が複雑になっていることが見て取れます。
イメージとしては「プロットしたとき真ん中に来るデータ」が種類Bになってほしいのに、これだと「ほとんどが種類Aだと判定される」ことになっています。
これはちょっと過学習しているように見えます。
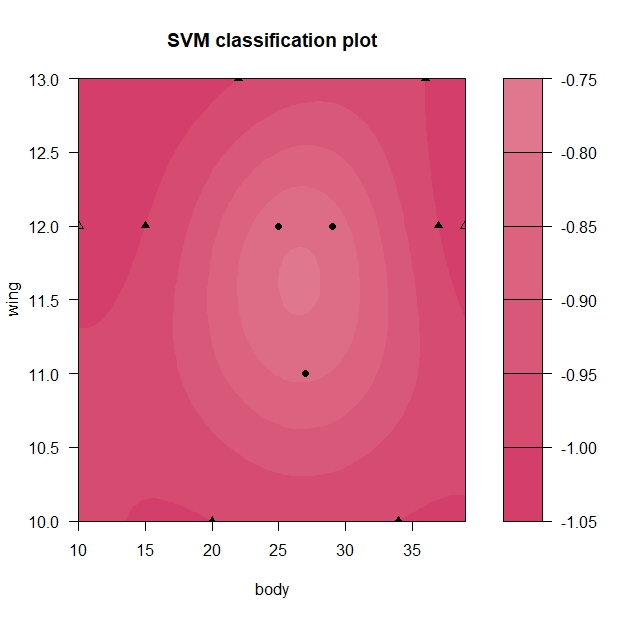
次は逆に汎化性能を上げすぎて、うまく分類できない例を載せます。
sigmaは1にして、パラメタCを0.01まで小さくしてみます。
# 非線形のSV分類 # rbfdot(ガウシアンカーネル) # Cを減らした svm_bird_5 <- ksvm( type ~ wing + body, data=bird_2, type="C-svc", kernel="rbfdot", kpar = list(sigma=1), C=0.1 ) # 分類境界の図示 plot(svm_bird_5, data=bird_2)
真っ赤になってしまい、分類できていないことがわかります。
> # 結果 > fitted(svm_bird_5) [1] A A A A A A A A A A A Levels: A B
すべてを種類Aだと判別してしまいました。
これは「もともとのデータにはAが多かった」→「長期的に見てもAが多いはずだ」という情報だけを使って、羽や体の大きさをほとんど使わなくなったのが理由です。
汎化性能を上げるためには、「手持ちのデータ」を信じすぎないことは大事ですが、ある程度羽や体の大きさといった情報を使わなければ分類はできません。
この塩梅を調整するのが難しいところです。
補足:パラメタ推定の工夫とカーネルトリック
サポートベクトルマシンの実行や結果の解釈に関する知識は今まで説明した通りです。
ここからはサポートベクトルマシンが「どのように推定されているのか」という「計算方法」の説明に移ります。
ここから話がガラッと変わることに気をつけてください。
相対問題と主問題
まず、サポートベクトルマシンでは、以下の式を最小にするのだと説明しました。
$$\min \{ \frac{1}{マージン(サポートベクトルと境界線の距離)} + C \times{誤判別数} \}$$
これはその通りなのですが、実際はもう少し工夫をして計算しています。
工夫された計算のことを「相対問題を解く」と呼びます。
なお、上記に挙げた式を「主問題」と呼び、主問題に対応する相対問題を解くことにより、サポートベクトルマシンを推定します。
実際に上記の式を相対問題で表現するとどうなるか、といったことはここでは説明しませんが、計算を簡単にするためにこのような工夫がなされているのだということをまずは覚えておいてください。
写像と次元の呪い
次に、非線形なデータへの変換について説明します。
非線形なデータに対しては、あらかじめデータを変換しておくと説明しました。
しかし、実際のところ、データを変換するという計算をするのはとても困難です。
今回のデータであれば「羽の大きさ、体の大きさ」だけが説明変数でした。
なので、線形の分類モデルだった場合は、2次元の説明変数を使って、分類をしていたわけです。
この場合、非線形なデータに対応するため、2乗した結果を説明変数に追加しようと思った場合、以下のように説明変数の次元が増えます。
(羽、体、羽2、体2、羽×体)
2次元だったものが5次元に増えました。
10個の変数があれば、55次元まで増えます。
極端な話、10000個の説明変数があれば、50005000次元にまで増えてしまいます。
これだけ次元が増えてしまうと、まともに計算するのは無理そうです。
なので計算に工夫が必要となります。
カーネルトリック
実はというと、データの変換は行われていません。
「データを変換しないのに、変換したのと同じような結果が得られる」という不思議な計算手法(あるいは計算の”考え方”)がありまして、その名をカーネルトリックと呼びます。
先に、相対問題を解くことでモデルを推定すると説明しましたが、相対問題を解くことの大きなメリットは、このカーネルトリックが使えることにあります。
なので、「サポートベクトルマシンの考え方としては」データを非線形変換してから分類するというので間違いないわけですが、「実際の計算では」かなり工夫されたものが使われているよということです。
このカーネルトリックが使える変換式にはいくつかの条件があります。
その条件を満たした関数を「カーネル関数」と呼びます。
カーネル関数としては、Rでの例にも挙げた、以下の3つが有名です。
・線形カーネル:kernel=”vanilladot”
・多項式カーネル:kernel=”polydot”
・ガウシアンカーネル:kernel=”rbfdot”
もちろんこれ以外にもいくつもあり、また自分でオリジナルのカーネル関数を作ることも可能です。
詳細は参考文献に譲ります。
スポンサードリンク
2.サポートベクトル回帰の考え方
回帰問題と分類問題
今までは「カテゴリ」を予測する分類問題でした。
次からは「数量データ」を予測する回帰問題に移ります。
サポートベクトルマシンは分類と回帰とで計算の方法が大きく変わります。
しかし、その考え方は変わりません。
共に「明らかに正しく予測できているデータに関しては、どーでもいいので無視して、データを予測するのに必要となるサポートベクトルのみを使う」という発想で予測します。
回帰問題の場合は、予測誤差を工夫します。
それが「ε-不感損失関数」です
ε-不感損失関数
ε-不感損失関数は、下の図のように、-ε~+εまでの範囲内では、予測値と実測値がずれても「ずれはない。予測は当たっている」とみなす予測誤差です。
上のグラフは、横軸に「予測値 - 実測値」の残差を置き、縦軸に「予測誤差の大きさ」すなわち損失を載せています。
残差が-ε~+εまでの範囲内では、損失は0とみなされます。
残差がεを超えたら、損失として計上します。
なお、残差がεと同じ、あるいはεを超えてしまうデータをサポートベクトルとみなします。
このε‐不感損失関数が小さくなるようにモデルを推定します。
そのため、ε‐不感損失関数に影響を及ぼさないデータ(サポートベクトルではないデータ)は予測に使われません。
εの値は、予め決めておく必要があります。
サポートベクトル分類で設定するパラメタ(コストCや、ガウシアンカーネルの場合はsigmaなど)もそのまま使う(解釈は変わりません)ので、チューニングが必要です。
考え方としてはこれだけです。
非線形なデータに対してはカーネル関数を使うことにより対応ができます。
また、相対問題を解くことで効率的に計算を行うところも、サポートベクトル分類と同じです。
Rによる計算例:サポートベクトル回帰
Rでやってみます。
Rに組み込みの大気の組成データを対象とします。
引数に『epsilon』が増えたこと以外は特に変わりありません。
ガウシアンカーネルを用いて、非線形なデータにも対応できるようにしてあります。
2018年6月20日追記
コードが間違っていたので修正しました。
元のコードには『type=”C-svc”』がついていましたが、これは不要です。
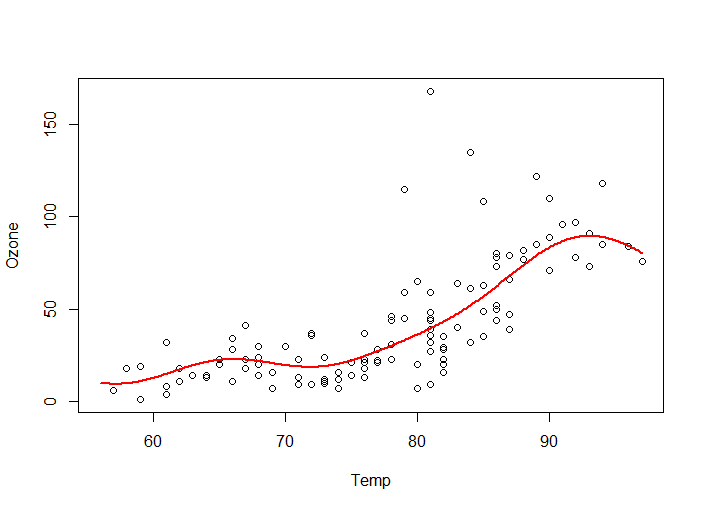
# 予測モデルの作成 svm_air <- ksvm( Ozone ~ Temp, data=airquality, epsilon=0.25, kernel="rbfdot", kpar=list(sigma=1), C=2 )
どんな結果になったか、予測結果を図示してみます。
# 予測 new <- data.frame( Temp=seq(min(airquality$Temp), max(airquality$Temp), 0.1) ) svm_air_pred <- predict(svm_air, new) # 予測結果の図示 plot( airquality$Ozone ~ airquality$Temp, xlab="Temp", ylab="Ozone" ) lines(svm_air_pred ~ as.matrix(new), col=2, lwd=2)
3.ハイパーパラメタのチューニング
最後に、ハイパーパラメタのチューニングをしてみます。
『Rによる機械学習:caretパッケージの使い方』でも説明をしていますが、caretパッケージを使うのが簡単です。
caretパッケージの詳細は、リンク先の記事を参照してください。
まずはcaretパッケージを使う準備から始めます。
# install.packages("caret")
# install.packages("e1071")
library(caret)
library(e1071)
# 並列化演算を行う
# install.packages("doParallel")
library(doParallel)
cl <- makePSOCKcluster(4)
registerDoParallel(cl)
『caret』だけでなく、並列化演算をするためのパッケージや、caretの内部でサポートベクトルマシンを計算するのに使われているパッケージなどをまとめてインストールしてください。
そのうえで、お手持ちのPCのコア数(コア数がわからなければ、『detectCores()』というRの関数を実行すれば簡単にわかるようです)を『makePSOCKcluster』関数の引数に入れれば、並列化演算ができます。
鳥の分類データをまた使って、チューニングしてみます。
# 鳥のデータ使ってチューニング
tuned_svm <- train(
type ~ wing + body,
data=bird_2,
method = "svmRadial",
tuneGrid = expand.grid(C=c(1:30), sigma=seq(0.1, 2, 0.1)),
preProcess = c('center', 'scale')
)
結果はこちら。
> tuned_svm
Support Vector Machines with Radial Basis Function Kernel
11 samples
2 predictor
2 classes: 'A', 'B'
Pre-processing: centered (2), scaled (2)
Resampling: Bootstrapped (25 reps)
Summary of sample sizes: 11, 11, 11, 11, 11, 11, ...
Resampling results across tuning parameters:
C sigma Accuracy Kappa
1 0.1 0.6125000 -0.04428438
1 0.2 0.6500000 0.06338899
1 0.3 0.6895833 0.16428571
1 0.4 0.7500000 0.36227273
1 0.5 0.8083333 0.47727273
・・・中略・・・
13 0.4 0.9708333 0.92712551
13 0.5 0.9708333 0.92712551
13 0.6 0.9812500 0.95344130
13 0.7 0.9708333 0.89712919
13 0.8 0.9569444 0.84449761
13 0.9 0.9256944 0.77727273
13 1.0 0.8805556 0.70227273
[ reached getOption("max.print") -- omitted 350 rows ]
Accuracy was used to select the optimal model using the largest value.
The final values used for the model were sigma = 0.6 and C = 4.
『sigma = 0.6 and C = 4』が最善ということがわかりました。
なお、計算するたびに、最適なパラメタが変わることがあります。
何回か試してみた方が安全かもしれません。
チューニングされたハイパーパラメタを使って、再度モデルを作り直して、境界線を図示してみます。
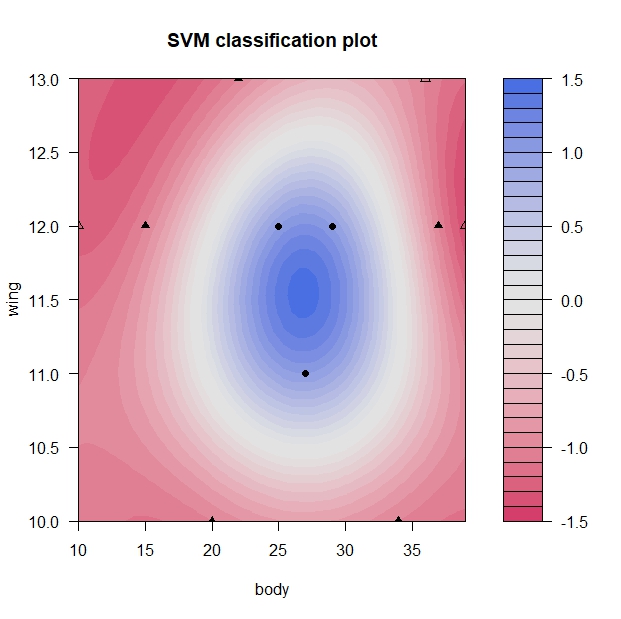
# 最も「よい」パラメタを使って境界線を図示 best_svm <- ksvm( type ~ wing + body, data=bird_2, type="C-svc", kernel="rbfdot", kpar = list(sigma=0.6), C=4 ) plot(best_svm, data=bird_2)
今回のようなサンプルデータですとたいした変化はないのですが、実際にサポートベクトルマシンを使って予測をしたい、という場合には、パラメタのチューニングはとても重要となってきます。
やり方だけ覚えておかれるとよろしいかと思います。
参考文献
|
サポートベクトルマシン (機械学習プロフェッショナルシリーズ) この一冊を読めば、サポートベクトルマシンのことは大体わかります。 いま、サポートベクトルマシンの勉強をしたいと思ったら、この本から始めるのが良いと思います。 |
 |
|
カーネル多変量解析―非線形データ解析の新しい展開 これもすごい本でして、カーネルトリックだのなんだのと難しい単語を一つ一つ丁寧に解説してくださっている良書です。 もしもこの記事を読んで、カーネル法に興味を持たれた場合は、是非一読をお勧めします。 |
 |
|
はじめてのパターン認識 サポートベクトルマシンに限らず様々な機械学習法が載った書籍です。 どのテーマも簡潔にまとまっている、この分野では有名な書籍です。 ただ、ちょっと簡潔すぎるかもしれません。 |
 |
スポンサードリンク
2017年7月24日:新規作成
2018年6月20日:サポートベクトル回帰のコードの修正と画像の差しかえなど


わかりやすい記事ありがとうございます。
サポートベクトル回帰の実行例の部分ですが、
type=“C-svc ”
となっているため、多クラス分類されているとおもいます。(Ozoneの値がクラス番号として扱われている?)
type指定を行わないか、svrのいずれかにすると、滑らかな曲線で回帰できます。
Hayakawa様
コメントありがとうございます。
管理人の馬場です。
大変お恥ずかしい間違いでして、確かにおっしゃる通りです。
失礼をいたしました。
修正をかけておきます。
ご指摘、ありがとうございました。