主成分分析の考え方

最終更新：2017年7月20日

主成分分析は、多種類のデータを要約するための強力なツールです。
この記事では、主成分分析の考え方・計算の方法、そしてR言語を用いた実装方法について説明します。
まずは、主成分分析とは何者で、計算結果をどのように解釈したらよいのかを学んでください。
そのうえで、ggplot2を使った美麗なグラフの作り方についても合わせて覚えていただければと思います。

コードはまとめてこちらに置いてあります。

スポンサードリンク

目次

1. 主成分分析の考え方
• 主成分分析とは何をするものか
• 主成分分析ができると何が嬉しいか
• 主成分分析の結果はどのように解釈すればよいか
• 寄与率
• 主成分得点
2. Rによる主成分分析
3. 主成分の計算方法
4. アヤメデータの分析例

 

1．主成分分析の考え方

主成分分析とは何をするものか

主成分分析とは何をするものでしょうか。
一言でいうと、下の図のように「散布図にそれっぽい線（軸）を引くこと」となります。

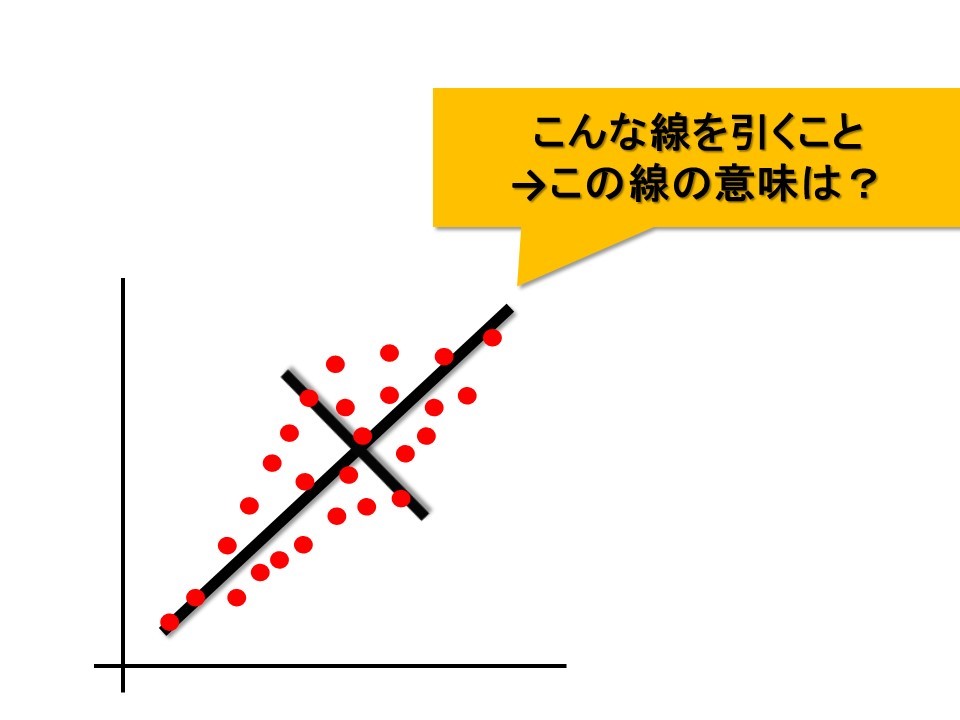
なお、赤い点がデータを表しており、主成分分析を通して引かれた黒くて太い線を主成分軸と呼びます。
さて、この線の意味はいったい何でしょうか。

 

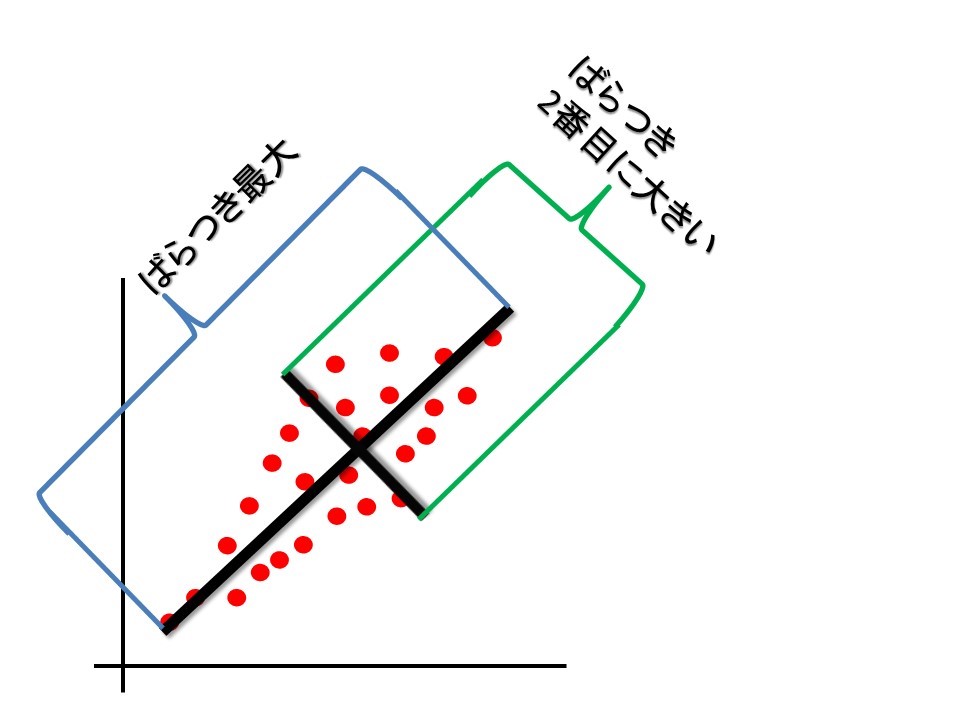
この線は、データのばらつき、すなわち分散を最大にするように引かれています。

分散という言葉が難しければ、散布図において「最も幅が広くなるように」線を引っ張たのだとご理解ください。
2本目の線は「2番目に幅が広くなるように」線が引かれています。
1番幅が広いものから順に、第1主成分軸、第2主成分軸……と呼ばれます。

この線が引っ張れると、とてもうれしいことがあります。
それは「データを一つ一つ見なくても、データの概要をつかむことができる」ことです。

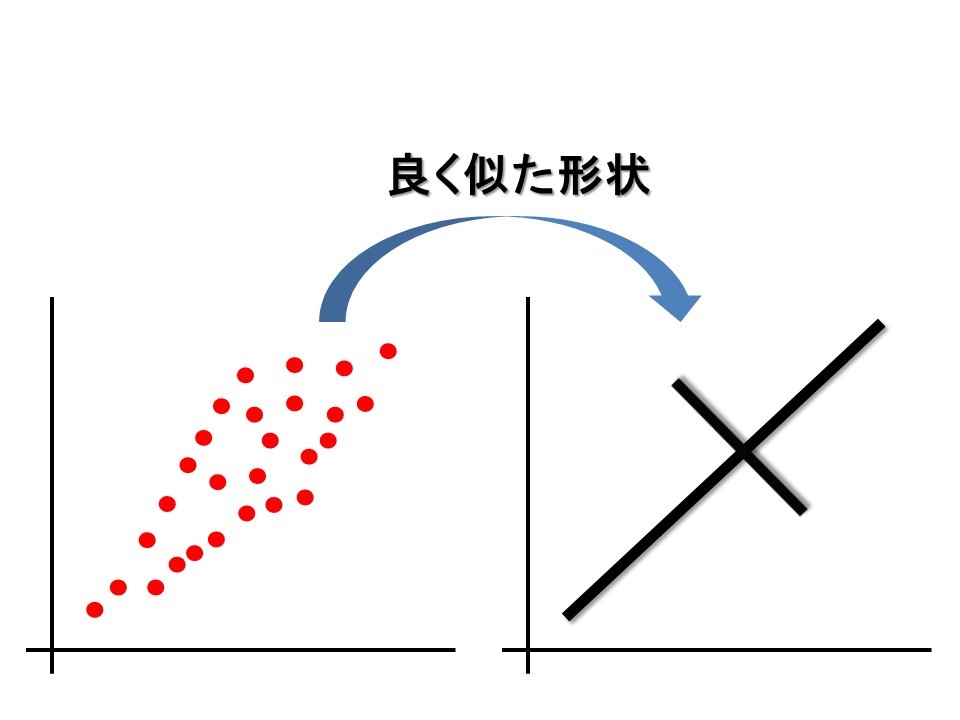
上の図を見てください。
赤い点が元のデータです。右のグラフが主成分分析を通して引かれた主成分軸です。
形がなんだかよく似ていますよね。
データをつぶさに見なくても、データの形状を「だいたいこんな感じ」と要約してくれる手法、それが主成分分析です。

主成分分析ができると何が嬉しいか

主成分分析ができると、データの要約ができます。
まずはデータの特徴を見てみたい、と思った際に、主成分分析は有力なツールとなります。

データの要約ができると、データの特徴を判断しやすくなります。
そのため、データのカテゴリ分けなどにも応用が可能です。

ユーザーのカテゴライズをしたいと思った時、どのように分析するでしょうか。
ユーザーの年齢や収入、購買頻度などなど様々な要素がデータとして蓄えられているはずです。
主成分分析ですと、様々な要素をひとまとめにできるので、例えば「収入が多く購買意欲も高いユーザー」など複数の要素を組み合わせて一つのカテゴリとして扱うことができるようになります。

後ほど実例を示しますが、主成分分析を使ったカテゴリ分けは、視覚的にもインパクトのあるものになります。

主成分分析の結果はどのように解釈すればよいか

寄与率

まず『データの要約』という観点から見ると、主成分軸の「寄与率」を理解することが重要です。

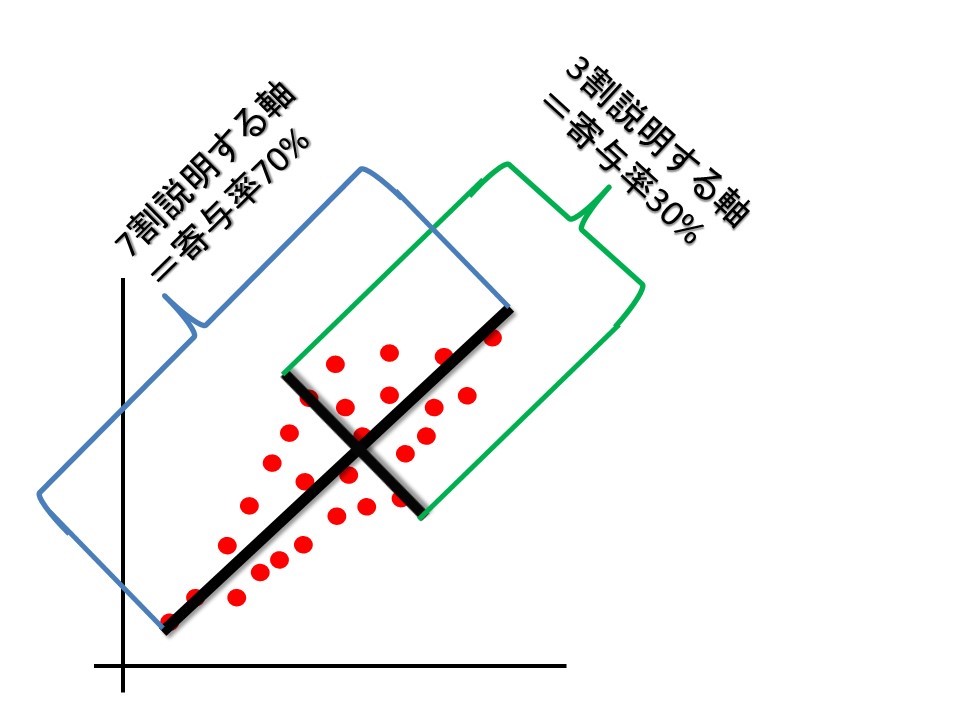
寄与率とは、下の図のように「この主成分軸一つで、データの何割を説明することができているか」を表したものです。

軸と寄与率の関係は、下の図を見るのがわかりよいです。
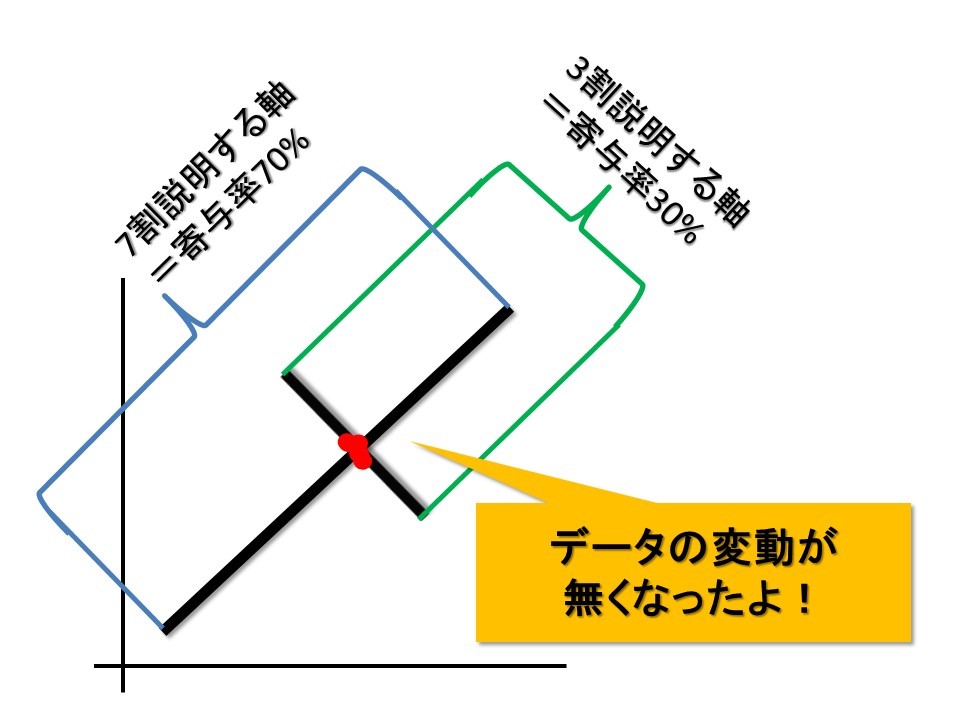
軸の真ん中にデータをぎゅっと持っていくと、データのばらつきが寄与率の分だけ減ります。

データが2次元であれば、2つの主成分軸を使えばデータの100%を説明することができます。
しかし、データが3次元以上であれば、2つの主成分軸だけですと、すべてを説明することができません。どれくらいを説明できているのかな、というのを見るときに寄与率は重要です。

主成分得点

主成分得点とは、主成分軸を基に、データをぐるっと回転させたときの座標に相当する値です。
第1主成分軸をPC1、第2主成分軸をPC2とすると、下の図のようになります。

 

2．Rによる主成分分析

Rで計算してみます。
コードはまとめてこちらに置いてあります。

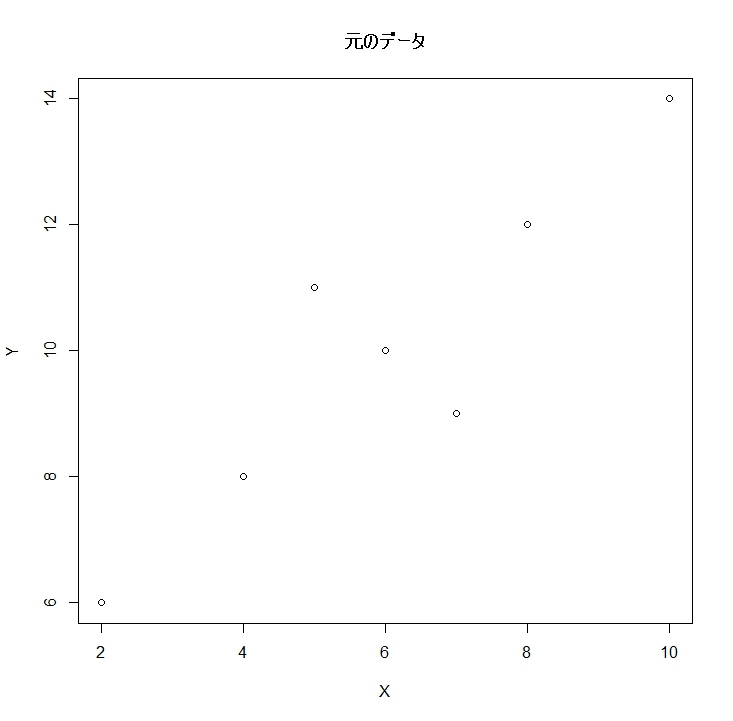
まずはデータを用意します。

# ---------------------------------------------------------
# 主成分分析の概要
# ---------------------------------------------------------

# サンプルデータ
sample_data <- data.frame(
  X = c(2,4, 6, 5,7, 8,10),
  Y = c(6,8,10,11,9,12,14)
)

plot(Y ~ X, data=sample_data)

分かりやすく十字の形をしたデータを作ってみました。

主成分分析を実行するのは簡単です。『prcomp』関数を使います。

# 主成分分析の実行
pcr_model_sample <- prcomp(sample_data, scale=T)

『prcomp』関数の中にデータを入れるだけです。
『scale=T』という指定はほぼ必須です。この引数の意味については、次節「主成分の計算方法」を参照してください。
ここでは計算のみ行います。

結果はこちら

> # 結果
> summary(pcr_model_sample)
Importance of components:
                          PC1     PC2
Standard deviation     1.3801 0.30861
Proportion of Variance 0.9524 0.04762
Cumulative Proportion  0.9524 1.00000
> 
> # 主成分得点
> pcr_model_sample$x
               PC1           PC2
[1,] -2.138090e+00  2.220446e-16
[2,] -1.069045e+00  1.110223e-16
[3,]  0.000000e+00  0.000000e+00
[4,]  5.551115e-17  5.345225e-01
[5,] -5.551115e-17 -5.345225e-01
[6,]  1.069045e+00 -1.110223e-16
[7,]  2.138090e+00 -2.259890e-16

『summary』関数を使うと主成分軸の寄与率などを見ることができます。
『Proportion of Variance』が各々の軸の寄与率で、寄与率の累積が『Cumulative Proportion』となっています。
これを見ると、第一主成分軸だけで95%以上も説明ができていることがわかります。

主成分得点は『$x』とつけてやることで抽出ができます。

主成分得点は、図示したほうがわかりよいです。
biplotという関数を使います。
元のデータと合わせて表示させてみます。

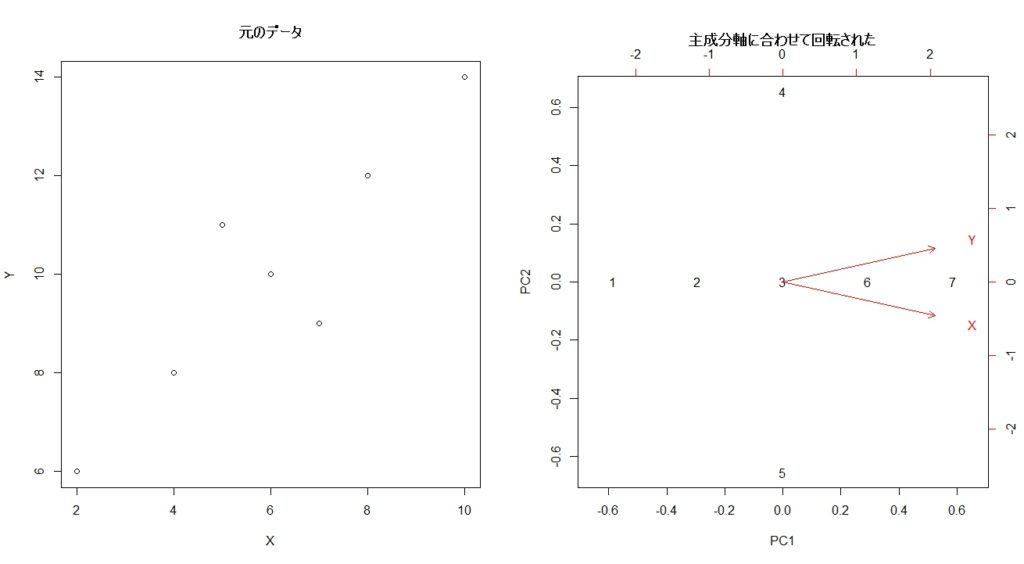
# 図示
par(mfrow=c(1,2))
plot(Y ~ X, data=sample_data, main="元のデータ")
biplot(pcr_model_sample, main="主成分軸に合わせて回転された")
par(mfrow=c(1,1))

グラフはクリックすると大きくなります。
右のグラフが主成分得点です。１～７までの数値が出ていますが、これは各データを表しています。
左側の元データだと右上に伸びていたグラフが、主成分得点だと回転されていることがわかります。

主成分得点のグラフ（上の右側のグラフ）に赤い線が引かれていますが、これはもともとの変数（このデータの場合はXやY）のもつ影響を図示したものです。
XもYも右側に伸びていますね。
元のデータを見ると（下のグラフ）、基本的には右肩上がりのデータとなっているので、Xが増えればYも増えるという関係にあります。なので左右（第一主成分軸）の向きは同じで、ともに右方向になっていました。
一方上下（第二主成分軸）で見ると、これは逆に右肩下がりになっています。XとYの方向性が変わる（Xが増えるとYが減る）ので、上下別の方向になっています。

今回のようなもともと2次元（データがXとYの2種類しかない）のデータだとただ回転されただけということになりますが、のちに見るように、変数が増えていくと、データを要約したうえで2次元のグラフに落とし込むことができるので、人間が解釈しやすくなります。

もちろん、画像データが相手だった場合は、画像を回転させることが目的という場合もあります。
そんな時にも、主成分分析の考え方を知っておくと便利です。

スポンサードリンク

 

3．主成分の計算方法

次は主成分軸や主成分得点がどのように計算されているのかを、簡単に説明します。
これはやや込み入った話題になるため、難しければ次の実践例にそのまま移ってもらっても結構です。

まず、主成分軸の計算方法を説明します。
これには2種類ありまして、1つが「分散共分散行列」の固有値問題を解く方法。もう1つが「相関行列」の固有値問題を解く方法です。

共分散も相関係数も、データ同士の関係を見るときに使われます。
ただし、共分散と違って、相関係数は「最大が１、最小が－１」と標準化されています。
そのため、例えばデータの単位がグラムとトンといったように異なっていたとしても、相関行列を使った場合ですと（標準化されているので）気にせずに解析をすることができます。
基本的には相関行列の固有値を計算するのが普通です。
先のRを使った計算例で『scale=T』と設定していました。これが「相関行列を使って、標準化されたデータに対して計算をしてくださいね」という指定です。
デフォルトでは（歴史的な事情があって）分散共分散行列を使った方法になっているようですので注意してください。

興味のある方は『Rのprcomp()関数で主成分分析をするときの注意点｜StatsBeginner: 初学者の統計学習ノート』というブログ様に事情が書かれてあったので、それを参照してください。

Rでも相関行列を計算したり、固有値問題を解いたりできるので、確認のためにやってみましょう。

まずは分散共分散行列と相関行列を計算してみます。

> # 分散共分散行列
> var(sample_data)
         X        Y
X 7.000000 6.333333
Y 6.333333 7.000000
> 
> # 相関行列
> cor(sample_data)
          X         Y
X 1.0000000 0.9047619
Y 0.9047619 1.0000000

これの固有値と固有ベクトルを求めることを「固有値問題を解く」といいます。

なぜ固有値問題を解くと主成分が求まるのか、直感的な説明はちょっと難しいのですが、以下のような流れがあるようです。

１：分散が最も大きくなるように線（主成分軸）を引く方法を数式であらわしてみた。
２：その式は、よく見ると、分散共分散行列（相関行列）に対して固有値問題を解いた時の固有ベクトルに等しいようだ

というわけで、やや天下り式ですが、相関行列の固有ベクトルを求めることによって、主成分軸がどうなるか調べてみます。

> # 主成分の固有ベクトル
> eigen_m <- eigen(cor(sample_data))
> eigen_m$vectors
          [,1]       [,2]
[1,] 0.7071068 -0.7071068
[2,] 0.7071068  0.7071068
> # 主成分分析の結果
> pcr_model_sample$rotation
        PC1        PC2
X 0.7071068 -0.7071068
Y 0.7071068  0.7071068

prcompの結果と一致していることを確認してください。

計算された固有ベクトルを使って、主成分得点を計算します。
元のデータに、相関行列の固有ベクトルを掛け合わせてやればOKです。

主成分分析の結果と合わせて図示してみます。

# データの回転と無相関化
sample_mat <- as.matrix(sample_data)

# 図示 
par(mfrow=c(1,2))
plot(
  sample_mat%*%eigen_m$vectors[,1], 
  sample_mat%*%eigen_m$vectors[,2], 
  main="固有ベクトルを使った回転"
)
plot(pcr_model_sample$x[,1], pcr_model_sample$x[,2], 
     main="主成分得点")
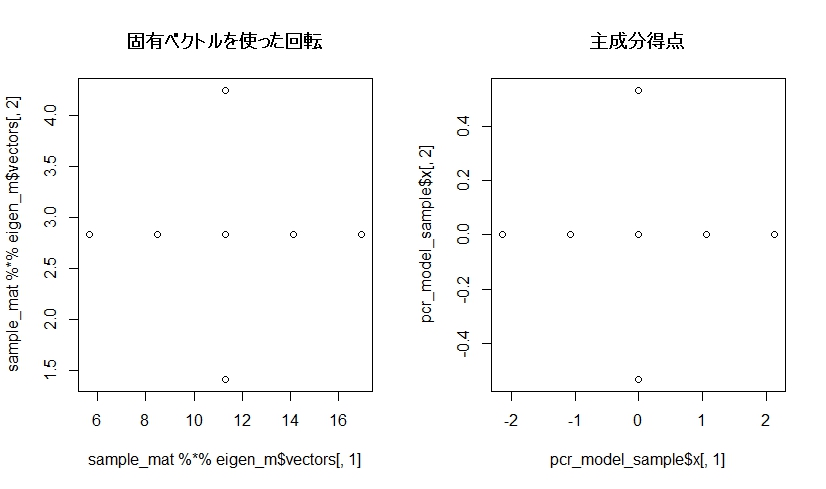
par(mfrow=c(1,1))

固有ベクトルを使った場合も、主成分得点と同じように、データが回転されているのがわかるかと思います。
なお、主成分得点は、データの標準化が別途行われているので、単位はあっていませんが、形状は同じになっています。

 

4．アヤメデータの分析例

次は、実践編として、アヤメデータの分析を試みます。
ggplot2というグラフを描くための便利パッケージを使った美麗なグラフの作り方も併せて覚えておいてください。

まずはアヤメデータの概要を見てみます。

> # アヤメの調査データ
> summary(iris)
  Sepal.Length    Sepal.Width     Petal.Length    Petal.Width          Species  
 Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100   setosa    :50  
 1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300   versicolor:50  
 Median :5.800   Median :3.000   Median :4.350   Median :1.300   virginica :50  
 Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199                  
 3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800                  
 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500              

ちょっとわかりにくいのですが、
Sepal：ガク
Petal：花弁
となっています。ガクや花弁の大きさを、アヤメの種類別にとった調査データです。

 

次に、アヤメデータがどのようなものか、散布図を並べて描いてみます。
このとき『ggplot2』と『GGally』という2つのパッケージをインストールすると、きれいなグラフが描けます。
このグラフを作る際には、『かっこいいいペアプロット図を描く｜DISTRICT 37』というブログ様を参照させていただきました。
必要に応じて、コメントアウトを外して、パッケージをインストールしてください。

## データの図示
# install.packages("ggplot2")
# install.packages("GGally")
library(ggplot2)
library(GGally)
ggpairs(iris, aes_string(colour="Species", alpha=0.5))

『ggpairs』という関数を使うのですが、その引数に『aes_string(colour=”Species”, alpha=0.5)』という指定を入れておくと、種類別に色分けができるようです。
なお、『alpha=0.5』というのは透明度の指定です。これを入れなければ、ちょっとベタっとした雰囲気になるというのと、データの重なりがあることに気づきにくくなります（少し透明にしておくと、データが重なった部分だけ色が濃くなる）。
ggolot2を使ったグラフですと、少し透明にしておくと見栄えが良くなるように思います。

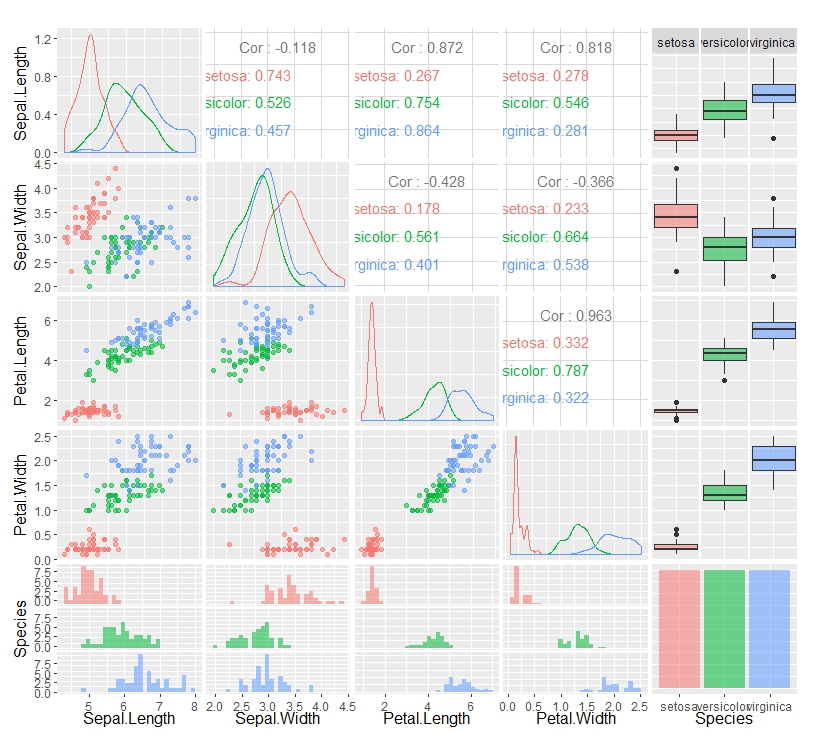
結果はこちら。
きれいなグラフが描けました。

グラフがたくさん出てきますが、これは各変数同士で個別にグラフを描画してくれているからです。
例えば2行1列目のグラフは、縦軸がSepal.Width（ガクの幅）、横軸がSepal.Length（ガクの長さ）の散布図となっています。以下同様に縦軸横軸の値を切り替えて複数のグラフを出してくれています。
1行1列目のように、横軸も縦軸も共に同じ変数になっていた場合は、その変数の、平滑化されたヒストグラムが描かれます。
5列目はすべて、アヤメの種類別の箱ひげ図になっています。

例えば2行1列目と1行2列目は、変数の組み合わせが同じになっていますね（共にSepal.Width（ガクの幅）とSepal.Length（ガクの長さ）が対応）。
この場合は、片方が散布図、もう片方が変数間の相関係数を表しています。
これを見ると、Sepal.Width(ガクの幅)だけが、ほかの変数との相関が低くなっていました。

また、4行目のグラフはアヤメの種類別・形質別のヒストグラムとなっています。
これもやはりSepal.Width(ガクの幅)だけ、他の変数と違って赤い（アヤメの種類がsetosa）ヒストグラムが右寄りになっています。

どうもSepal.Width(ガクの幅)だけはほかの変数と違っているようだ、という感覚を持ちつつ、次の分析に進みます。

 

本題の主成分分析に移ります。
prcompは、アヤメの種類のようなカテゴリデータに対しては適用することができません。
そのため、5列目の種類データを取り除いたデータを分析に使います。

## 主成分分析の実行
# 種類データを除く
pca_data <- iris[,-5]

# 主成分分析の実行
model_pca_iris <- prcomp(pca_data, scale=T)

 

結果はこちら。
第二主成分軸までで、全体の95%以上を説明することができているようです。

> # 結果
> summary(model_pca_iris)
Importance of components:
                          PC1    PC2     PC3     PC4
Standard deviation     1.7084 0.9560 0.38309 0.14393
Proportion of Variance 0.7296 0.2285 0.03669 0.00518
Cumulative Proportion  0.7296 0.9581 0.99482 1.00000

 

最後に、主成分得点を図示します。

単に図示をするだけでなく、ggplot2を援用したきれいなグラフを作ってみました。
そのためには『ggbiplot』というパッケージをインストールする必要があります。
しかし、この『ggbiplot』はCRANには登録されていないようで、普通に『install.packages』を使うとエラーになります。
そこで、先に『devtools』というパッケージをインストールします。これでGithubというソースコード管理サービスサイトから直接パッケージをインストールすることができるようになります。
『devtools::install_github(“vqv/ggbiplot”)』とすることで『ggbiplot』のインストール完了です。

# 主成分分析の結果をグラフに描く
# install.packages("devtools")
# devtools::install_github("vqv/ggbiplot")
library(ggbiplot)

ggbiplot(
  model_pca_iris, 
  obs.scale = 1, 
  var.scale = 1, 
  groups = iris$Species, 
  ellipse = TRUE, 
  circle = TRUE,
  alpha=0.5
)

グラフの描画には『ggbiplot』関数を使います。
引数には、データだけでなく、標準化を行うかどうかの指定なども行います。
『groups = iris$Species』とすると、アヤメの種類別に色分けをしてくれます。
『ellipse』や『circle』をTにしておくと、グラフに円を描いてくれます。これがあった方がより見やすくなるように感じます。

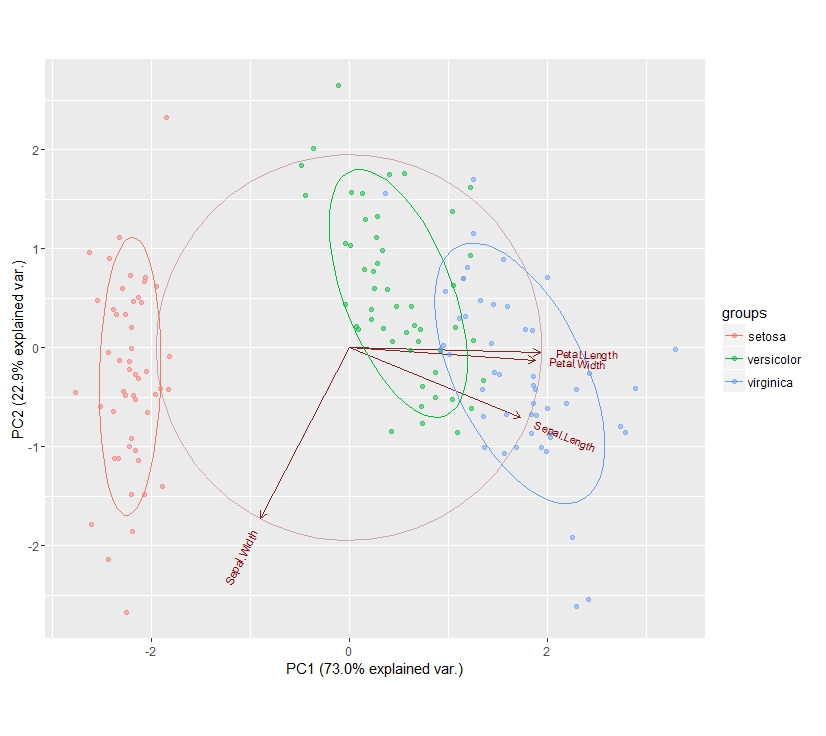
まずは、アヤメの種類別にはっきりと分かれました。
種別に楕円が引かれているので、その特徴が一目でわかります。

矢印で引かれた、各変数の方向性を確認してください。
左右が第一主成分を表しており、Petal.Length（花弁の長さ）・Petal.Width（花弁の幅）はほぼ同じ方向に矢印が伸びています。
両者は「ほぼ同じ意味を持つ変数である」ことがわかります。両方とも花弁ですので言われてみればその通りという気もします。
それと少し離れますが、やはり右方向にSepal.Length（ガクの長さ）が伸びています。
この3つの変数は大体似たような意味を持っており、それがまとめられて第一主成分軸になったのだということがわかります。

一方ggpairsでもやや特殊だと思われていたSepal.Width（ガクの幅）は、やはり一人だけアサッテの方向に矢印が伸びています。
これが第二主成分軸を形作っていることに注目してください。
アヤメの分類の際は、Sepal.Width（ガクの幅）と、それ以外、というまとまりでデータを見るのがよさそうだということがわかりました。

今回の事例ですと、アヤメをどのような形質を使って分類すればよいのか、という示唆が与えられました。
しかし、あまりに便利すぎて「やろうと思えばいろいろな解釈ができてしまう」ということもあります。
同じグラフを見ても、人によって解釈が異なるという場合もしばしば。自分に都合が良いところだけを抜き出して説明する人もいなくはないです。
解釈の方法を学ぶことで、誤解をしないようにすることも大事かと思います。

生き物の分類に限らず、たくさんの種類の変数をどのようにまとめればいいか、まとめた結果をどのように解釈すればよいかを考える際に、主成分分析は強力なツールになります。
誤用・乱用に気を付けて、一つのツールと割り切って使うようにしてください。

主成分分析のパワーアップバージョンとしては以下のものがあります。
興味のある方は調べてみてください。

• 対応分析：カテゴリデータなどにも適用可能
• カーネル主成分分析：非線形なデータにも適用可能
• 主成分回帰：主成分分析をした結果を使って、回帰分析を行い、予測を行う

 

参考文献

はじめてのパターン認識   主成分分析に限らず様々な機械学習法が載った書籍です。 どのテーマも簡潔にまとまっている、この分野では有名な書籍です。

Rによるデータサイエンス データ解析の基礎から最新手法まで   R言語を使った分析の手法がほぼ網羅されている本です。 もちろん主成分分析の解説もあります。

書籍以外の参考文献

・タコでもわかる主成分分析
　→管理人が学生の時、このサイトをみて勉強した記憶があります。主成分分析の詳細を知りたい方はぜひこのサイトを見てください。

・Rのprcomp()関数で主成分分析をするときの注意点｜StatsBeginner: 初学者の統計学習ノート
　→prcomp関数の使い方に詳しい記事です

・かっこいいいペアプロット図を描く｜DISTRICT 37
　→ggpairs関数を使うときに参考にさせてもらいました。

・A biplot based on ggplot2
　→ggbiplotのコードはこちらから見れます。

スポンサードリンク