カイ二乗検定
最終更新:2020年12月27日
χ二乗検定(カイ二乗検定・χ
また、より正確な検定とされる「Fisherの正確確率検定」の実行方法や、データの誤った集計がもたらす問題である「シンプソンのパラドクス」も説明します。
ABテストなどでもよく使われるχ二乗検定の仕組みと、ExcelやRを用いた実際の計算方法を理解してください。
2018年4月19日追記
拙著「Pythonで学ぶあたらしい統計学の教科書」の発売に合わせて、Pythonでの実行方法を加筆しました。
スポンサードリンク
目次
- χ二乗検定の目的
- χ二乗検定の考え方
- ソフトを使ったχ二乗検定の計算
- Excelによる計算
- Rによる計算
- Pythonによる計算
- Fisherの正確確率検定
- シンプソンのパラドクス
1.χ二乗検定の目的
χ二乗検定は別名「独立性の検定」とも呼ばれます。
独立という言葉はやや難しいのですが「独立→関係がない」「独立でない→何か関係性がある」と解釈してもらえれば結構です。
よく言われる例として「長男であるかどうかは、野球選手の適正と何か関係があるか」というお話があります。
野球選手のうち、長男と次男のどちらのほうが人数が多いかを調べてみると、長男のほうが多かったそうです。
仮に、以下のようなデータが手に入ったとしましょう。
| 野球選手の人数 | |
| 長男 | 50 |
| 次男 | 20 |
これを見ると、「ああ、やっぱり長男のほうが多かったのだな」ということがわかります。
だから「野球選手には、長男のほうが向いているのか」と考えてしまうかもしれません。
長男だと責任感があるので、仕事をしっかりとやりきることができ、野球選手としても優秀な選手になりやすいのだと。次男はダメだから、野球はやらせないでおこうと。このような考察をしてしまうかもしれません。
ですが、このデータには致命的な欠陥があります。
それは「野球選手にならなかった人のデータが無い」ことです。
データを取り直すと、こうなりました。
| 野球選手の人数 | 選手以外の人数 | 合計 | |
| 長男 | 50 | 499950 | 500000 |
| 次男 | 20 | 199980 | 200000 |
| 合計 | 70 | 699930 | 700000 |
長男であろうと、次男であろうと100000分の1の割合で野球選手になっていることがわかります。
すなわち、長男であろうと次男であろうと、野球選手になれる割合は変わらないということです。
何のことはありません。
長男だけがいて、次男がいない家庭はあります。お子さんが一人しか生まれなかったときですね。
しかし、その逆、長男はいないのに次男だけいるという家庭はあり得ません。
なので、長男のほうが、その人数がもともと多かったわけです。だから、野球選手になっている人も多かった。
このように、「何か関係性があるかどうか」を調べるということは、データ分析のだいご味であると同時に、間違った結論を導き出しやすい作業でもあります。
そこで出てくるのが、独立性の検定です。
独立性の検定を行うためには、まずはデータの集計が必要です。
先ほどのようなデータの集計を「クロス集計表」と呼びます。
クロス集計表の威力(長男・次男の例を見ればわかりますね)を理解することがまずは第一歩です。
その次に「本当に関係があるかどうか、微妙なデータ」が現れたときに、今度は検定を行います。
例えば、ウェブサイトのデザインを検討するためのABテストを実施していて、以下のようなデータが得られたとします。
| ボタン押した | 押さなかった | 合計 | |
| 青いボタン | 70 | 180 | 250 |
| 赤いボタン | 30 | 120 | 150 |
| 合計 | 100 | 300 | 400 |
青いボタンがいいのか、赤いボタンがいいのか、あるいは「どちらでもいい」のか、難しいところです。
そこで出てくるのが「統計的仮説検定」という枠組みです。今回ではその中でもχ二乗検定という手法を学びます。
これを使えば「ボタンの色を変えることは、ボタンの押されやすさと関係がある」ということが証明できるかもしれません。
2.χ二乗検定の考え方
χ二乗検定では、以下のステップを踏んで検定を行います。
- データをクロス集計表にまとめる
- 期待度数(もし関係が無かったら、きっとこうなるだろうという回数)を求める
- データと期待度数との差を求める(この差が大きければ、関係ありとみなせそう)
- χ二乗値を求める
- χ二乗値をp値に変換する
- p値を解釈する
順に行きましょう。
1.データをクロス集計表にまとめる
これは、もうすでに集計できているという前提で進めます。
以下の、ウェブサイトにおける、ボタンの色と押されやすさの関係を調べたデータを使います。
| ボタン押した | 押さなかった | 合計 | |
| 青いボタン | 70 | 180 | 250 |
| 赤いボタン | 30 | 120 | 150 |
| 合計 | 100 | 300 | 400 |
2.期待度数(もし関係が無かったら、きっとこうなるだろうという回数)を求める
次に「もし関係が無かったら、きっとこうなるだろうという回数」を求めます。
これを期待度数と呼びます。
この期待度数と、元のデータが大きく異なるというのであれば「関係ありそう」だとみなせそうですね。
期待度数の求め方を説明します。
まず、青いボタンに注目します。青いボタンを目にした人の数は「250人」です。
次に「ボタンの色に関わらない、ボタンを押した人の割合」を見ます。全体400人のうち、100人がボタンを押していますね。
なので「もしもボタンの色と押されやすさに関係がないのだとしたら、4分の1の割合でボタンが押されるのだ!」ということになるわけです。
というわけで、「もしもボタンの色と押されやすさに関係がないのだとしたら、青いボタンを押す人の数は、250÷4=62.5人になるだろう」と計算できます。
この62.5人が期待度数となります。
赤いボタンも同様に、150人のうちの4分の1がボタンを押すので、「37.5人」と求まります。
「(ボタンの色を無視して)ボタンを押さなかった人の割合」は4分の3となっていますね。
なので、青いボタンを押さなかった人は「250×(3/4)=187.5人」
同様に、赤いボタンを押さなかった人は「150×(3/4)=112.5人」となります。
これをまとめると、以下のようになります。
| ボタン押した | 押さなかった | 合計 | |
| 青いボタン | 62.5 | 187.5 | 250 |
| 赤いボタン | 37.5 | 112.5 | 150 |
| 合計 | 100 | 300 | 400 |
3.データと期待度数との差を求める
元データと期待度数の違いを、以下の式を使って計算します。
$$\frac{ (元データ – 期待度数)^2 }{期待度数}$$
例えば青いボタンを押した人の数はこうなっていました。
元データ:70人
期待度数:62.5人
よって、以下のように計算できます。
$$\frac{(70 – 62.5)^2}{62.5} = 0.9$$
これをすべて計算したら、以下の表のようになります。
| ボタン押した | 押さなかった | |
| 青いボタン | 0.9 | 0.3 |
| 赤いボタン | 1.5 | 0.5 |
4.χ二乗値を求める
χ二乗値は、単に、先ほど計算した表の中身を足し合わせるだけで計算できます。
$$0.9+0.3+1.5+0.5= 3.2$$
というわけで、3.2となりました。
この値が大きければ大きいほど、期待度数と元データが大きく異なっていることになります。
期待度数は「もし関係が無かったら、きっとこうなるだろうという回数」のことです。
なので、χ二乗値が大きければ「ボタンの色と押されやすさには関係がありそうだ」とみなすことができるわけです。
この考え方はぜひ覚えておいてください。
5.χ二乗値をp値に変換する
χ二乗値が大きければ「ボタンの色と押されやすさには関係がありそうだ」とみなすことができることがわかりました。
次の問題は「χ二乗値がいくらになれば『大きい』と判断できるか」という基準を定めることです。
3を超えれば大きいとみなせるのか、4を超えなきゃダメなのか、難しいところです。
そこで、「統計的仮説検定」という枠組みが使われるわけです。
χ二乗値を計算すると、p値と呼ばれる値に変換できます。
変換です。
χ二乗値がわかっていれば、p値には(パソコンを使って計算すれば)すぐに変換できます。
χ二乗値が大きくなれば、p値は小さくなります。
そして、p値は基準が定まっています。p値は0.05を下回れば小さいとみなす、と伝統的に決まっています。
というわけで、
- χ二乗値をp値に変換する
- χ二乗値が大きければ、p値は小さくなる
- p値が0.05を下回るくらい小さければ、χ二乗値は十分大きいといえる
上記の3ステップを踏むことで、χ二乗値の大小判定ができます。
この変換は、Excelなどを使えば簡単に計算できます。
後ほど詳細を説明しますが、『CHISQ.DIST.RT()』というExcelの関数を使います(Excel2007以前の場合は『CHIDIST』関数を使います)。
『=CHISQ.DIST.RT(3.2, 1)』とセルに入力すると、0.074という数値が返ってきます。
p値=0.074であり、0.05を上回ってしまいました。
このときは「ボタンの色と押されやすさには、有意な関係があるとは言えない」ということになります。
6.p値を解釈する
p値とは何でしょうか。
データを分析する際にとても怖いのが「たまたまそうなった」という「たまたま」あるいは「偶然」です。
「たまたま」青いボタンが好きな人が被験者の中に多かったとか、「たまたま」皆赤いボタンが嫌いな人だけが集まっていたとか、そんなユーザーでテストをしていた可能性もなくはないわけです。
こんなユーザーのもとで集められたデータを使うと、「たまたま」青いボタンが押されやすいように見えてしまい、χ二乗値も大きくなってしまうでしょう。
そんな「たまたま、色とボタンの押されやすさに関係があると見えてしまう確率」がp値です。
もっと極端な例を挙げます。
集計の際、うっかりして、ボタンの色を記録するのを忘れてしまいました。
そこで、得られたデータを「ランダムに」青いボタン、赤いボタンと後付けで書いておきました。
こんなひどいデータですと「青いボタンと赤いボタンの違い」が出てくるはずがありませんね。だって、両方を一緒くたにして集計してしまっているんですから。
でも、「たまたま、まぐれで」χ二乗値が3.2よりも大きくなることはあり得ます。
じゃあその確率はどれほどかというと「0.074=7.4%」くらい、となるわけです。
少々荒い定義ですが、p値とは「たまたま、χ二乗値が○○よりも大きくなる確率」であると覚えておくとよろしいかと思います。
補足:帰無仮説・対立仮説
ここからは、統計学の専門用語の解説となります。
実務に使う際ならば、上述の知識で何とかなりますので、難しければ飛ばしてください。
今回の場合は、以下のようになります。
帰無仮説:ボタンの色によって、押されやすさは変わらない
対立仮説:ボタンの色によって、押されやすさが変わる
対立仮説は「私たちが立証したい仮説」のことです。
帰無仮説はその逆だと思えばわかりよいです。
補足:検定の非対称性
なぜ帰無仮説というものをいちいち置くのかというと、その原因が検定の非対称性にあります。
検定は「帰無仮説が異なっている」ということの立証はできます。
p値が0.05以下になれば、帰無仮説が異なっているとみなすわけです。
でも「仮説が正しい」と主張することはできません。違うことが言えるだけです。
これを検定の非対称性と呼びます。
なので、「p値が0.05より大きかったので、帰無仮説が間違っているといえなかった」からといって「帰無仮説は正しい」とはならないことに注意してください。
違っていることの立証はできますが、正しいことの立証はできません。
それが統計的仮説検定です。
スポンサードリンク
3.ソフトを使ったχ二乗検定の計算
χ二乗検定の計算は、ExcelやR言語を使えば簡単に計算ができます。
順に説明します。
1.Excelによる計算
まずはExcelですが、計算用のExcelファイルを置いておきました。
Excel2010以上で使えます。
chisq-test.xlsx
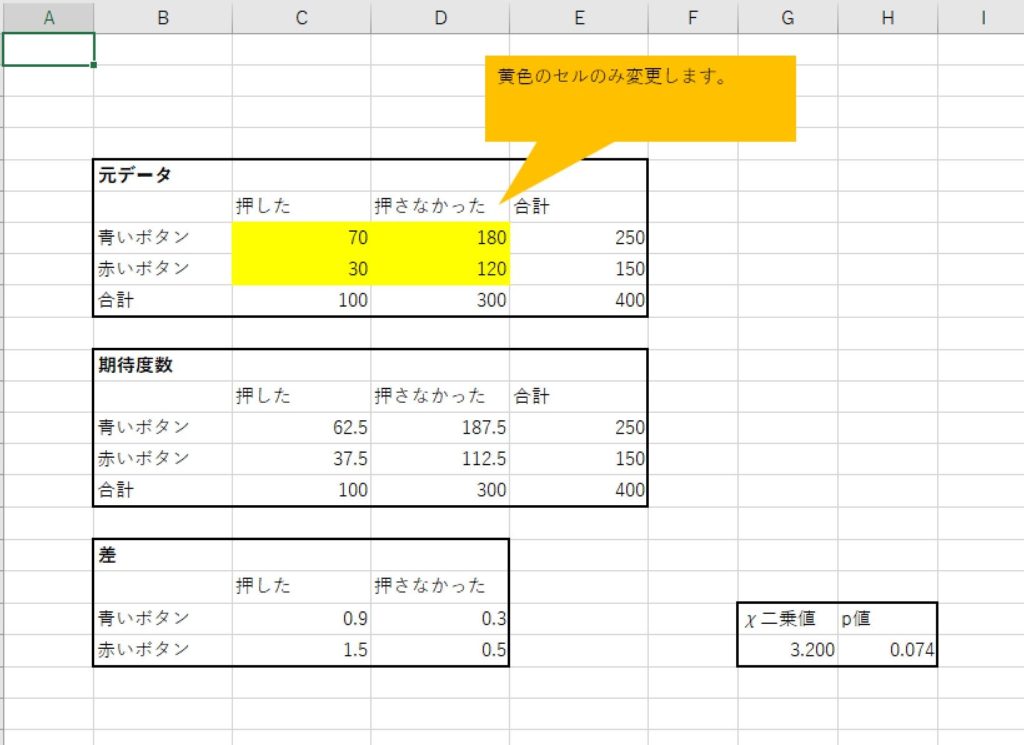
このファイルには、以下の図のようなシートが入っています。
コメントが入っていますが、黄色いセルの数値を変えると、χ二乗値とp値が自動で計算されます。
なお、20行H列には『=CHISQ.DIST.RT(G20,1)』という数式が入っています。
これはExcel2010以降でしか動きません。
Excel2007以前のバージョンを使う場合は『=CHIDIST(G20,1)』に置き換えてください。
2.Rによる計算
R言語に詳しくない方は、まずは『Rの簡単な使い方』を参照することをお勧めします。
Rはプログラムを書く必要があるためちょっと面倒ではあるのですが、後ほど説明するFisherの正確確率検定などの高度な計算をするならば、むしろこちらのほうが早く計算ができます。
まずは、データを用意します。
Rの場合は、data.frameという関数を使います。
# データを用意する
ABtest_data <- data.frame(
button = c("blue", "blue", "red", "red"),
result = c("press", "not","press", "not"),
number = c(70, 180, 30, 120)
)
こんなデータになっています。
> # データの中身 > ABtest_data button result number 1 blue press 70 2 blue not 180 3 red press 30 4 red not 120
なお、このデータの形式は、整然データなどと呼ばれます。
この形式でデータを保存しておくと、たとえデータの変換が必要となっても簡単にできるので、お勧めです。
続いて、これをクロス集計表に変換します。
xtabsという関数を使います。
# クロス集計表に変換 cross_data <- xtabs(number ~ ., ABtest_data)
こんな結果になっています。
> # データの中身
> cross_data
result
button not press
blue 180 70
red 120 30
最後に、χ二乗検定を実行します。
『chisq.test』という関数を使います。
> # χ二乗検定の実行 > chisq.test(cross_data, correct=F) Pearson's Chi-squared test data: cross_data X-squared = 3.2, df = 1, p-value = 0.07364
『X-squared = 3.2』で、χ二乗値が3.2であること、
『p-value = 0.07364』でp値が0.074ほどであることがわかります。
Excelの結果と一致していることを確認してください。
3.Pythonによる計算
人気のプログラミング言語であるPythonを使っても、簡単に検定を実行することができます。
Pythonをまだ触ったことがないという方は『Pythonの簡単な使い方』を参照してください。
Jupyter Notebookの使用を前提とします。実行結果をまとめたものは『chisq-test.html』から参照することができます。レポートのように簡単に結果を残せるのはJupyter Notebookの利点です。
まずは必要なライブラリのインポートを行います。
実はnumpyなどの使わないのも入ってるんですが、これらは分析においてしばしば必要となるので、一括でインポートしておくと便利です。
表示桁数の指定もしておきました。
# 必要なライブラリのインポート import numpy as np import pandas as pd import scipy as sp from scipy import stats # 表示桁数の指定 %precision 3
データを用意します。pandasのDataFrameという形式とします。
# データを用意する
ab_test_data = pd.DataFrame({
"button":["blue", "blue", "red", "red"],
"result":["press", "not","press", "not"],
"number":[70, 180, 30, 120]
})
print(ab_test_data)
このような結果になっています。
button number result 0 blue 70 press 1 blue 180 not 2 red 30 press 3 red 120 not
このデータをクロス集計表に変換します。
# クロス集計表に変換する
cross_data = pd.pivot_table(
data = ab_test_data,
values ="number",
aggfunc = "sum",
index = "button",
columns = "result"
)
print(cross_data)
このような結果になっています。
result not press button blue 180 70 red 120 30
検定を行います。
scipy.statsのchi2_contingency関数を使います。基本的な検定はscipy.statsを使えば済むことが多いです。
引数には対象となるデータと、補正を行わないという指定をします。
# カイ二乗検定の実行 stats.chi2_contingency(cross_data, correction=False)
以下のような結果になります。
(3.200, 0.074, 1, array([[ 187.5, 62.5],
[ 112.5, 37.5]]))
出力は左から順番に、以下のようになっています。
・カイ二乗統計量
・p値
・自由度
・期待度数の表
4.Fisherの正確確率検定
次は、やや発展的な話題として、Fisherの正確確率検定について説明します。
名前に「正確確率」と書いてあるので、その名の通り、確率を正確に計算してくれます。
確率とはもちろんp値のことです。
p値とは「たまたま、χ二乗値が○○よりも大きくなる確率」であったことを思い出してください。
この確率を正確に計算します。
χ二乗検定は、実はというと、「近似的に」p値を計算していました。
具体的には「χ二乗値をp値に変換する」というあたりの計算が怪しいわけです。
そのため、サンプルサイズ(調査したデータの数)が200を超えていない場合は、なるべく使わない方が良いといわれています。
そんなときに使うのが、Fisherの正確確率検定です。
これは並び替え(数え上げ)検定の一種です。ノンパラメトリック検定の一種といってもよいです。
今回得られたデータを再掲します。
| ボタン押した | 押さなかった | 合計 | |
| 青いボタン | 70 | 180 | 250 |
| 赤いボタン | 30 | 120 | 150 |
| 合計 | 100 | 300 | 400 |
さて、データは400個ありますね。
この400このデータを4つのマスに自由に入れていいとしたら、何パターンできるか、計算できますか。
ちょっと面倒なのですが、公式があります。
| ボタン押した | 押さなかった | |
| 青いボタン | A | B |
| 赤いボタン | C | D |
$$\frac{ {}_{(A+C)} \mathrm{ C }_A \times {}_{(B+D)} \mathrm{ C }_B }{ {}_{(A+B+C+D)} \mathrm{ C }_{(A+B)} }$$
順列組合せは覚えていますでしょうか。Combinationの「C」なので、順番は無視した組み合わせですね。
これで、どの升目に入るか、そのパターンを網羅することができます。
この数を「全パターン数」と呼ぶことにします。
次に気になるのは「今回のデータよりも、もっと極端なデータが得られる場合の数」です。
極端なデータというのは、例えば、以下のデータがわかりよいでしょう。
| ボタン押した | 押さなかった | 合計 | |
| 青いボタン | 250 | 0 | 250 |
| 赤いボタン | 0 | 150 | 150 |
| 合計 | 250 | 150 | 400 |
こんなデータが出てこれば、「絶対に、色によって、ボタンの押されやすさが変わるだろう」と分かりますね。
こんな「手持ちのデータよりも、より”極端に”ボタンの押されやすさが変わるデータは、何パターンあるか」を調べます。
この数を「極端パターン数」と呼ぶことにします。
ここまでくれば、最後に
極端パターン数 ÷ 全パターン数
としてやれば、「今回のデータよりも、より”極端に”効果があるとみなせるデータが得られる確率」が計算できますね。
言い換えると「まぐれで、今回のデータよりも効果が高いとみなせるデータが得られる確率」がわかるわけです。
これをp値とするのがFisherの正確確率検定です。
p値が小さければ、まぐれではないんだと主張できますね。
近似的な手法を使わず、すべて数え上げで計算をするので、p値が正確に求まります。サンプルサイズが小さくても支障ありません。
その代り、計算が大変です。
特に、「手持ちのデータよりも、より”極端に”ボタンの押されやすさが変わるデータは、何パターンあるか」を数え上げるのが大変ですね。
これは、できればコンピュータにやってもらいたいところです。
そこで、R言語の出番です。
Rを使えば簡単に計算ができます。
(Excelではちょっと難しい)
やってみましょう。
χ二乗検定と同じデータを使います。
『fisher.test』という関数を使います。
> # Fisherの正確確率検定 > fisher.test(cross_data) Fisher's Exact Test for Count Data data: cross_data p-value = 0.07529 alternative hypothesis: true odds ratio is not equal to 1 95 percent confidence interval: 0.3808254 1.0692355 sample estimates: odds ratio 0.643552
『p-value = 0.07529』となっていたので、χ二乗検定とだいたい同じ結果となりました。
やはり有意な関係があるとは言えないという結果です。
なお、χ二乗検定のパワーアップバージョンとしてG検定などもありますが、基本的にはFisherの正確確率検定が最も正確にp値を計算できますので、これだけ覚えておけばよいかと思います。
今回のように、複雑な計算をする場合はExcelよりもRのほうが簡単です。
Rをまだ触ったことがないという方は、この機会にぜひRの使い方を学んでください。
無料のソフトですし、文献も豊富です。
今回は「統計的仮説検定」に絞って解説をしていきました。
検定は便利なのですが、使える範囲が絞られてきます(検定の非対称性があるので「仮説が正しい」と主張することができないのはなかなかやりにくいものです)。
もっと、広く柔軟にデータを分析する方法として「統計モデル」という考え方が普及しています。
特に一般化線形モデルは文献も多く、Rを使えば簡単に計算ができます。一般化線形モデルを使えば、χ二乗検定と同じ目的の計算を別のやり方で行う方法がわかるでしょう(対数線形モデルと呼ばれます)。
統計学において、何をどこまで学ぶのかは、個人の意思が尊重されるべきだと思います。
しかし、もしも統計学を深く学んでみたいという方がこの記事を読まれていたら、ぜひ「統計的仮説検定のその次」へ進んでいただければと思います。
キーワードは統計モデル、そして一般化線形モデルです。この辺がわかれば、また次の技術へ移っていくこともできるでしょう。
より発展的な話題としてベイズ統計学も挙げられます。
詳しくは、下で挙げた参考文献を読んでみてください。
5.シンプソンのパラドクス
最後に、注意してほしい問題としてシンプソンのパラドクスを説明します。
これは「関係がないとわかっているデータを足し合わせると、なぜか関係があるように見えてしまう」という不思議なパラドクスです。
データの集計の仕方がずさんですと起こりうる問題ですので、ぜひ注意してください。
例えば、「データ1」のようなデータがあったとします。
これは、ボタンの押されやすさは、色によって、まったく変わっていませんね。
| ボタン押した | 押さなかった | |
| 青いボタン | 10 | 50 |
| 赤いボタン | 10 | 50 |
一方、「データ2」ようなデータがあったとします。
これもやはり、色によって、ボタンの押されやすさは変わりません。
| ボタン押した | 押さなかった | |
| 青いボタン | 10 | 10 |
| 赤いボタン | 200 | 200 |
この2つのデータを合計します。
| ボタン押した | 押さなかった | |
| 青いボタン | 20 | 60 |
| 赤いボタン | 210 | 250 |
これに対してFisherの正確確率検定を実行します。
> # シンプソンのパラドクス
> # データを用意する
> paradox_data <- data.frame(
+ button = c("blue", "blue", "red", "red"),
+ result = c("press", "not","press", "not"),
+ number = c(20, 60, 210, 250)
+ )
> cross_paradox_data <- xtabs(number ~ ., paradox_data)
> fisher.test(cross_paradox_data)
Fisher's Exact Test for Count Data
data: cross_paradox_data
p-value = 0.0005554
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
1.439711 4.557334
sample estimates:
odds ratio
2.51598
『p-value = 0.0005554』とあるように、p値が0.05を下回りました。
帰無仮説は棄却され、有意な関係性があるとみなすべきところです。
データ1も、データ2も、ともに「色によって、押されやすさはまったく変わらないデータ」でした。
けれども、このデータを合わせると、なぜか「有意な関係性」が現れます。
これをシンプソンのパラドクスと呼びます。
こんな問題があるので、不用意にデータを集計しないように気を付けなければなりません。
参考文献
|
Pythonで学ぶあたらしい統計学の教科書 このサイトの管理人が書いた本です。 確率変数・確率分布や、数量データ・カテゴリデータの違いといった基本から、統計モデル・機械学習といった応用まで学びます。 紹介ページはこちら。 出版社サイトはこちら。 |
 |
|
生物学を学ぶ人のための統計のはなし Fisherの正確確率検定やシンプソンのパラドクスの解説が載っている本です。 特にFisherの正確確率検定の説明がとても丁寧です。これ以外にも、検定の仕組み、p値の計算方法が丁寧に載っています。 初学者の方にはぜひ一読をお勧めします。 |
 |
|
マンガでわかる統計学 ベストセラーとなっている統計学の入門書です。 漫画ですが、内容はしっかりしており、入門に最適です。 χ二乗検定についても1章かけて説明がされています。 |
 |
|
データ解析のための統計モデリング入門―― 一般化線形モデル・階層ベイズモデル・MCMC 統計的仮説検定の「次」に行きたい方にお勧めする、新しい統計学の入門書です。 統計学について、より突っ込んで学んでみたい方にお勧めします。 |
 |
|
平均・分散から始める一般化線形モデル入門 このサイトの管理人が書いた本です。 平均や分散といった基本から、一般化線形モデルまで解説しています。 この記事は第7部第3章「Rによる対数線形モデル」を大幅に加筆修正して作成されたものです。 サポートページはこちら。 |
「平均・分散から始める一般化線形モデル入門」を購入されるときの注意
定価は2500円(消費税8%で2700円)ですが、Amazonさんなどでは在庫が不足しており、中古価格が高騰しています。
重版したので出版社には在庫が残っています。出版社のサイトからですと送料無料・書籍代は後払い・最短翌日出荷で、確実に定価で手に入ります。
以下のネット書店も併せてご利用ください。
|
|
|
|
|
スポンサードリンク
更新履歴
2017年7月13日:新規追加
2018年4月19日:Pythonでの実行方法を追記
2020年12月27日:「関連する記事」のリンクを修正(本文の変更は無し)



こんにちは。
丁寧な解説、ありがとうございます。
統計分析が統計分析が得意でない私にも
カイ二乗検定がどういうものか、よくわかりました。
「カイ二乗検定すれば良いよ」と言われたけど、なんだかわかんなくって
困っていたので大変助かりました。
ありがとうございます☆
丁寧な解説ありがとうございます。
卒業論文の分析の際に、使わせていただきます。
コメントありがとうございます。
お役に立てたようで何よりです。
理系の研究者ですが統計が苦手です。査読依頼を受けた論文の統計解析が理解できず困っていました。
こちらの説明は凄くわかりやすかったです。拒絶反応が出ずに最後まで読めました。
これまで本やwebサイトで調べた経験上、一番わかりやすかったです。ありがとうございました。
あみ様
コメントありがとうございます。
管理人の馬場です。
そのように言っていただけると、当方としても励みになります。
ありがとうございます。
L作物 M作物 N作物 合計
A地域 50% 30% 20% 100%
B地域 30% 40% 30% 100%
計 80% 70% 50% 200%
以上のクロス集計(%表示)は2行×3列ですが、A、B両地域間の作物選択比率の違いをどのように検定したらよいでしょうか?
坂本様
コメントありがとうございます。
管理人の馬場です。
χ二乗検定は、2×3のクロス集計でも適用可能です。
例えば以下のようにすれば、検定ができます。
(以下の計算では、%ではなく、合計数が200であると想定。)
# データを用意する
qhisq_test_data <- data.frame(
area = c("A", "B", "A", "B", "A", "B"),
species = c("L", "L", "M", "M", "N", "N"),
number = c(50, 30, 30, 40, 20, 30)
)
# クロス集計表に変換
cross_data <- xtabs(number ~ ., qhisq_test_data)
# 結果
chisq.test(cross_data, correct=F)
Pearson's Chi-squared test
data: cross_data
X-squared = 8.4286, df = 2, p-value = 0.01478