時系列分析

HOME
１．予測理論
時系列分析
ARIMAモデルによる株価の予測

2017年7月14日 / 最終更新日時 : 2017年7月14日馬場真哉時系列分析

ARIMAモデルによる株価の予測

最終更新：2017年7月14日

標準的な時系列解析手法であるARIMAモデルを用いた、株価の予測とその評価の方法について説明します。
ARIMAモデルは、R言語を使うととても簡単に推定することができます。
簡単である割には、予測精度は高く、時系列予測における標準的な手法となっています。

この記事では、株価のデータに対して、ARIMAモデルを推定し、株価を予測することを試みます。
株価を予測することはとても難しいので、この手法を使えばすぐに利益が出るということはあり得ません。
しかし、時系列データの取り扱いとARIMAモデルの推定、そして予測の評価という一連の流れを学ぶことで、ほかのデータなどに対して応用する能力が身につくかと思います。

コードはまとめてこちらに置いてあります。

スポンサードリンク

1．時系列解析とARIMAモデル

時系列解析とは、過去と未来の関係性を明らかにする解析手法のことです。
昨日の株価が高ければ明日も高くなるだろう、とか、その逆に、昨日の株価が高ければ今日は値下がりする、といった関係性を調べ、将来の予測をします。

ARIMAモデルは別名「自己回帰和分移動平均モデル」とも呼ばれる、時系列解析の手法の一つです。
詳しくは『時系列解析_理論編』を参照してください。
ここでは概要を説明するにとどめます。

ARIMAモデルはAR・I・MAの3つに分かれます。

AR:自己回帰モデル(ARモデル)
MA:移動平均モデル(MAモデル)
I:和分過程

自己回帰モデルと移動平均モデルは、各々単体でも予測に使うことのできる時系列モデルです。
2期前までのデータを使う自己回帰モデルを『AR(2)』と記します。p期前までのデータを使うならば『AR(p)』と表します。
同様に、q期前までのデータを使う移動平均モデルを『MA(q)』と表します。
両方をくっつけたものが『ARMA(p,q)』と呼ばれるモデルです。
pやqといった指定を「次数」とも呼びます。
次数が大きい方が、過去の長い期間を予測に使えますが、モデルとしては複雑になります。

自己回帰モデルと移動平均モデルの両方を組み合わせることによって、様々な時系列データに適用ができる柔軟なモデルを作ることができます。
また、過去のデータのうち、どれだけの期間を使うか（すなわちpやqをいくらにするか）を変えることによっても、挙動を変えることができます。

Iは何回和分かを表す部分です。
I(d)で、d階和分であることを表します。

和分とは、「和」ですので、足し合わせるという意味です。
例えば「１，２，３，４」の1階和分は「１，１＋２，１＋２＋３，１＋２＋３＋４」となります。

例えばARIMA(p,1,q)というモデルは「ARMA(p,q)モデルであらわされるデータの1階和分系列である」と解釈されます。
和分系列のままだと扱いが難しいですので、差分をとってから解析するのが普通です。

まとめます。
ARモデル・MAモデル共に、単体でも予測に使うことのできる時系列モデルです。
両者を合わせたARMAモデルは高い予測力を持ちます。
ARIMAモデルは、データの差分をとってからARMAモデルを推定したものです。
差分をとってデータを整形することで、ARMAモデルを正しく推定できるようにしています。

2．株価の取得

『Rによる株式データの取得とグラフの描画』と同じやり方で、『株価データサイト k-db.com』様からデータを取得します。

株価取得関数はこちらに置いておきました。
この関数をコピペして使ってもらってもよいですし、以下のコードのようにsource関数を使って読み込んでもらっても構いません。

やってみます。
コードはまとめてこちらに置いてあります。

# -----------------------------------------------------------------------
# 株価の取得
# -----------------------------------------------------------------------

# 株価取得関数の読み込み
source("https://logics-of-blue.com/wp-content/uploads/2017/07/getstockData.txt")

# みずほHGの株価を取得する
mizuho <- getStockFromKdb(8411, 2016:2017)

『source(“読み込み元になるファイル名”)』とすれば、関数を読み込んでいつでも使えるようにしておくことができます。
『getStockFromKdb』という管理人の自作関数を読み込んだので、それを使って、証券コード・西暦の2つを指定して、データを取得しました。

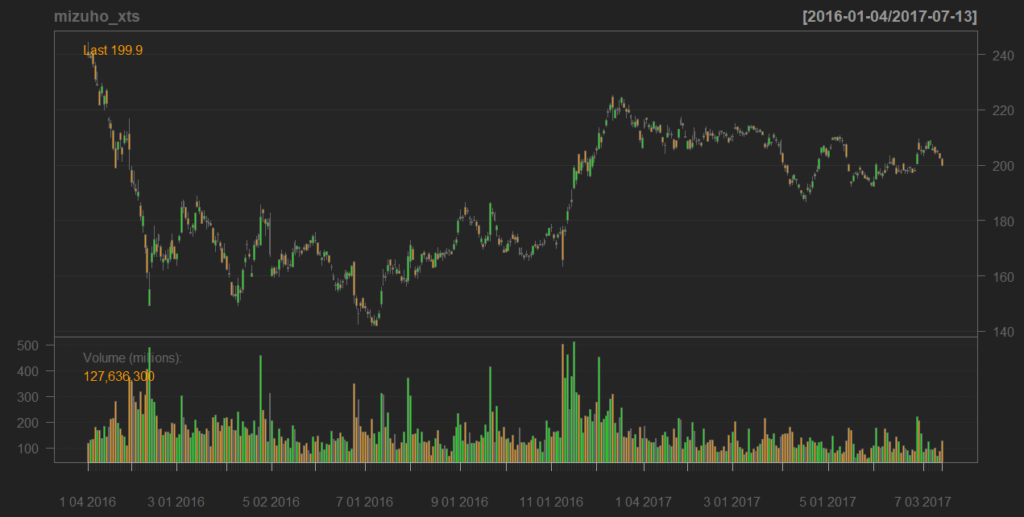
図示してみます。
『quantmod』というパッケージをあらかじめインストールしてから実行してください。

# install.packages("quantmod")
library(quantmod)

# xts形式に変換(1列目は証券コードなので削除)
mizuho_xts <- as.xts(read.zoo(mizuho[,-1]))

# ローソク足のグラフを描く
chartSeries(
  mizuho_xts, 
  type="candlesticks"
)

結果はこちら。
簡単にローソク足が描けます。

最後に、対数をとってから、差分系列にしておきました。
そのうえで、訓練データとテストデータに分けます。

# 対数差分系列にする
log_diff <- diff(log(mizuho_xts$Close))[-1]

# 訓練データとテストデータに分ける
train <- log_diff["::2017-06-30"]

test <- log_diff["2017-07-01::"]

対数差分系列は、和分系列を元に戻すという意味と、対数をとることで、データを正規分布に合わせるという意味があります。
対数差分系列は、近似的には「変化率」と同じ意味合いを持つので、解釈がしやすいことも利点です。

スポンサードリンク

3．ARIMAモデルの推定と予測の評価

続いて、ARIMAモデルの推定に移ります。

forecastパッケージの『auto.arima』関数を使います。
必要ならばforecastパッケージをインストールしてから実行してください。

# -----------------------------------------------------------------------
# ARIMAモデルによる予測
# -----------------------------------------------------------------------

# install.packages("forecast")
library(forecast)

# ARIMAモデルの推定
model_arima <- auto.arima(
  train,
  ic="aic",
  stepwise=F,
  approximation=F,
  max.p=10, 
  max.q=10,
  max.order=20,
  parallel=T,
  num.cores=4
)

計算にやや時間がかかるので注意してください。

9行目からがモデルの推定なのですが、かなり設定事項が多いですので、10行目から順に説明します。

train：訓練データ
ic=”aic”：モデル選択の規準としてAICを使う

ARIMA(p,d,q)のpやd、qといった次数を決めることをモデル選択と呼びます
AICはよく使われるモデル選択の規準です。予測精度が高くなるようにモデルを選んでくれます
AIC以外にもBIC(bicと指定)やAICC(aicc)が使えます

stepwise=F:計算をケチらず、すべての「p,q」を網羅的に調べろという指定
approximation=F:計算の簡略化を行わないという指定
max.p=10:ARモデルの最大次数
max.q=10:MAモデルの最大次数
max.order=20:p+dの最大値の指定

max.p・max.q・max.orderの3つを合わせてモデル選択の範囲を指定しています
これによりARMA(0,0)~ARMA(1,0)~ARMA(10,0)~ARMA(0,10)~ARMA(10,10)までをすべての次数で総当たり的に計算してくれます
和分過程か否かは、内部で単位根検定という手法を使って勝手に判断してくれるので、設定は不要です（だからdは指定しなくてOK）
今回は当たりませんが、季節変動を取り込んだモデルだった場合は、『max.order』で、ARMAの次数＋季節変動の次数の合計値を指定します（季節変動は、今回は関係ありませんので0次となっています。なので、今回の例では無視できました。季節変動が入ったモデルの場合は注意してください）

parallel=T:計算を並列化して早くするという指定
num.cores=4:並列化の際のコア数

4にしてあるのは管理人のPCに合わせてあります。お手持ちのPCのコア数を調べて数値を変えてください

推定結果はこちらです。

> # 推定結果
> model_arima
Series: train 
ARIMA(1,0,0) with zero mean     

Coefficients:
         ar1
      0.0973
s.e.  0.0519

sigma^2 estimated as 0.0003984:  log likelihood=916.17
AIC=-1828.34   AICc=-1828.31   BIC=-1820.53

『ARIMA(1,0,0)』ですので、『AR(1)』となり、実質、ただの自己回帰モデルと同じモデルが選ばれました。
最大でARIMA(10,1,10)まで候補となっているはずですが、かなり単純なものが選ばれたことになります。

予測してみます。
『予測の評価方法』にも書きましたが、ナイーブな予測（複雑な計算を行わない単純な予測）と比較するために、ナイーブな予測の予測結果も出しておきます。

# 予測
f_arima <- forecast(model_arima, h=9)

# ナイーブな予測も併せて作成
f_rw <- rwf(train)
f_mean <- meanf(train)

rwfは「翌日は、前日と同じ株価」であると予測します。
meanfは「翌日は、今までの株価の平均値」であると予測します。

テストデータにおける予測精度を見てみます。

> # 予測精度の比較
> accuracy(f_arima, test)
                        ME        RMSE         MAE      MPE     MAPE      MASE         ACF1
Training set -0.0003802122 0.019933919 0.014236900      NaN      Inf 0.7219092 0.0003382555
Test set     -0.0029983004 0.008267393 0.006872747 96.81261 96.81261 0.3484958           NA
> accuracy(f_rw, test)
                        ME        RMSE         MAE      MPE     MAPE      MASE       ACF1
Training set -1.707034e-06 0.026945080 0.019721179      NaN      Inf 1.0000000 -0.4487635
Test set     -1.556285e-03 0.007853496 0.006616477 70.98416 115.3637 0.3355011         NA
> accuracy(f_mean, test)
                        ME        RMSE         MAE      MPE     MAPE      MASE
Training set  2.600406e-19 0.020025090 0.014231330      Inf      Inf 1.0000000
Test set     -2.594997e-03 0.008123385 0.006746598 91.63447 91.63447 0.4740666

上から順番に、ARIMAモデル・「翌日は、前日（テストデータの場合は、訓練データの最終日）と同じ株価」・「翌日は、今までの株価の平均値」という予測の精度となっています。
一番わかりよいのが『RMSE』です。これが小さければ小さい方が、予測精度が高いです。

見ると、ARIMAモデルは、訓練データにおける予測精度は3つの中で最も高いものの、テストデータにおいては、予測精度が最も悪くなっていることがわかります。
ちょっと厳しい言い方をすると「ARIMAモデルは、予測の役に立たなかった」ということができます。
ARIMAモデルで予測した結果をそのまま使って、株式投資を行うことには無理がありそうです。

4．一期先の予測の繰り返し

このままですとARIMAダメだったね、で終わってしまうので、もう少し工夫します。
ARIMA(1,0,0)が選ばれたモデルでした。理論上はこれが最も予測精度が良いはずですが、過去1日のデータしか予測に使われていません。
このモデルで、長期(9日)の予測をしたのが問題なのかもしれませんね。

そこで、1日先の予測のみの評価をすることにします。
で、1日経ったら、訓練データをスライドさせるのです。

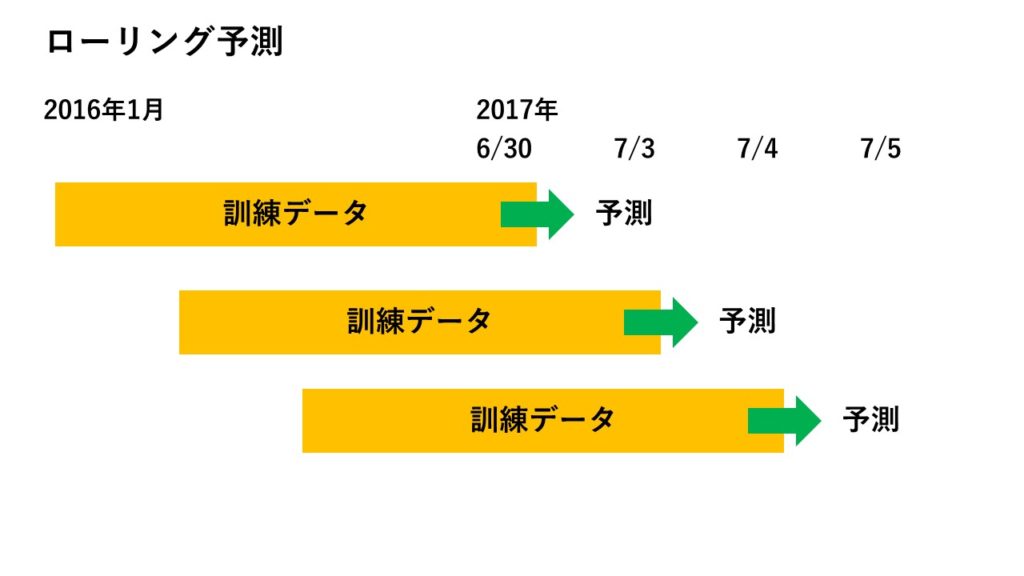
こんなイメージです。
7月3日の予測：7月2日以前のすべてのデータを使って、7月3日のみを予測する
7月4日の予測：訓練データの最も古いデータを捨てて、代わりに7月3日のデータを訓練データに入れる。そして1日先を予測する
……以下その繰り返し。

図にすると、こうなります。

普通にコードを書くと、ちょっと面倒なのですが、xtsパッケージには、その名も『rollapply』という便利関数があるので、それを使います。

まずは、準備として、「データを入れると、すぐに1期先の予測値を出してくれる関数」を作ります。

# データを入れると、1期先の予測をしてくれる関数
calcForecast <- function(data){
  model <- Arima(data, order=c(1,0,0))
  return(forecast(model,h=1)$mean)
}

訓練データの長さは367個あるようでしたので、367単位でスライドさせていけばOKです。

> # 訓練データの長さ
> length(train)
[1] 367

やってみます。

## 一期先予測
f_arima_2 <- rollapply(log_diff, 367, calcForecast)

# 1期先の予測値なので、実際の日付とずれている。
# lagを使って実際の日付に合わせる
f_arima_2 <- lag(f_arima_2)

# NAを消す
f_arima_2<- f_arima_2[!is.na(f_arima_2)]

まず、ローリング予測をした段階ですと「6月30日(訓練データ最終日）」に「7月3日（テストデータ最初日）」の予測値が入っています。
日付が一日ずれていますね。
それをlag関数を使って戻します。

さらに、最初の367日間はNAとなって計算ができない（あたりまえですが、データが無いので）ので、これを消しました。

同様に、平均値予測と「翌日は、前日と同じ株価」とするナイーブな予測も計算します。

# 平均値予測
f_mean_2 <- rollapply(log_diff, 367, mean)
# 1期先の予測値なので、実際の日付とずれている。
# lagを使って実際の日付に合わせる
f_mean_2 <- lag(f_mean_2)
# NAを消す
f_mean_2 <- f_mean_2[!is.na(f_mean_2)]
f_mean_2

# 1期前予測
f_rw_2 <- lag(log_diff["2017-06-30::"])
f_rw_2<- f_rw_2[!is.na(f_rw_2)]

予測精度はこちら。

> # 予測精度
> accuracy(as.ts(f_arima_2), test)
                   ME        RMSE         MAE      MPE     MAPE
Test set -0.002554879 0.007983168 0.006752174 93.66284 95.22182
> accuracy(as.ts(f_mean_2), test)
                   ME        RMSE         MAE      MPE     MAPE
Test set -0.002706925 0.008209062 0.006821828 92.14742 92.14742
> accuracy(as.ts(f_rw_2), test)
                   ME        RMSE        MAE      MPE     MAPE
Test set -0.001328539 0.008619336 0.00670267 106.0518 157.0582

ようやくこれで、ARIMAモデルは、ナイーブな予測の予測精度を（わずかに）超えました。
RMSEはARIMAモデルが最小となっています。

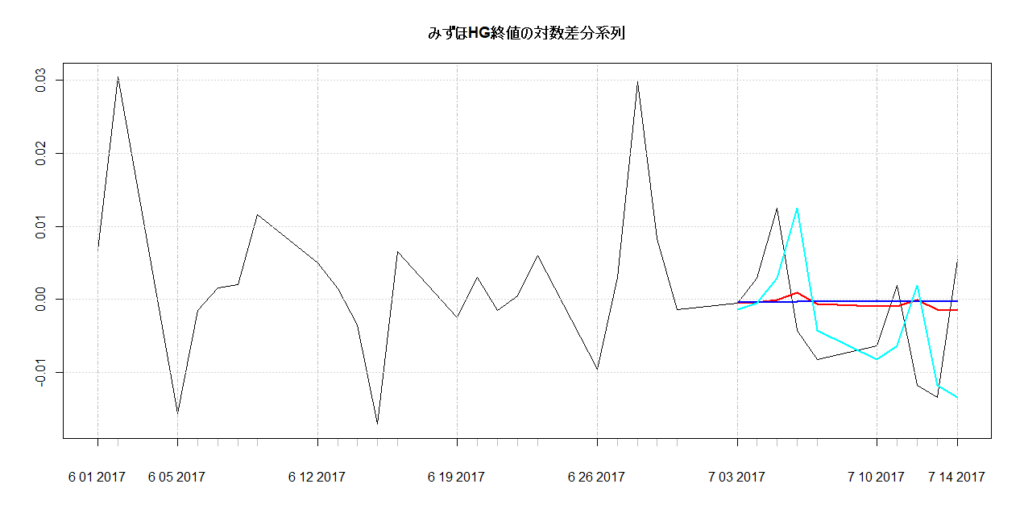
図示してみます。

# 図示
plot(log_diff["2017-06::"], main="みずほHG終値の対数差分系列")
lines(f_arima_2, col=2, lwd=2)
lines(f_mean_2, col=4, lwd=2)
lines(f_rw_2, col=5, lwd=2)

結果はこちら。

赤い線がARIMAの予測結果ですが、あまりぱっとしない感じはあります。
ARIMAモデルですとこれが限界のようですね。

参考文献

金融データ解析の基礎

金融時系列解析に特化した書籍です。
xtsの使い方やquantmodの使い方に加えて、ARMAやGARCHといった時系列モデルの解説も載っています。

現場ですぐ使える時系列データ分析

R言語を使った時系列分析の方法が書かれた書籍です。
ファイナンスの話題も多く載っています。

Rとトレード ――確率と統計のガイドブック

R言語を用いた証券投資分析の方法が書かれた本です。
Rの基礎から、確率統計の基礎、金融データ分析の基礎、そして株取引のためのプログラミング方法まで幅広く載っている書籍です。

経済・ファイナンスデータの計量時系列分析

このサイトで、時系列解析の記事を書いた時はほぼ必ず紹介している良書です。
ARIMAモデルなどの時系列モデルの解説が載っている書籍です。

スポンサードリンク

コメントを残すコメントをキャンセル

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。

データ分析入門

2017年7月13日

データ分析入門

2017年7月18日

ARIMAモデルによる株価の予測

目次

1．時系列解析とARIMAモデル

2．株価の取得

3．ARIMAモデルの推定と予測の評価

4．一期先の予測の繰り返し

参考文献

コメントを残すコメントをキャンセル

カイ二乗検定

t検定の考え方

目次

1．時系列解析とARIMAモデル

2．株価の取得

3．ARIMAモデルの推定と予測の評価

4．一期先の予測の繰り返し

参考文献

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル