予測の評価方法：誤差の指標とナイーブな予測

時系列分析を使って予測をするのは良いのですが、やみくもに複雑な手法を使って「計算したことに満足してしまう」というのはぜひ避けたいですね。
ここではR言語の「forecast」パッケージを使って、予測の評価をする方法を説明します。

予測の評価における原理原則を理解したうえで、R言語を使った実践の方法を学んでください。
ソースコードはこちらから見れます。

クロスバリデーション法を使った予測の評価は『R言語による時系列予測とクロスバリデーション法による評価』を参照してください。

スポンサードリンク

目次

1. 予測評価の原理原則
2. 予測誤差の指標
3. ナイーブな予測１：ホワイトノイズ
4. ナイーブな予測２：ランダムウォーク
5. 意思決定と予測の評価

 

1．予測評価の原理原則

時系列予測に限らず、予測評価における原則があります。
覚えておいてほしい原則は以下の2つです。

1．訓練データとテストデータは分ける

2．ナイーブな予測との差を評価する

順に説明します。

1．訓練データとテストデータは分ける

予測をする際には、予測モデルを作る必要があります。
予測モデルを作るためには、予測モデルの中で使われるパラメタを推定しなければなりません。

パラメタ推定の時に使われるデータが「訓練データ」です。

例えば「月ごとの売り上げ」をパラメタとして、来年のビールの年間売り上げを予測するとしましょう。
データは2000年と2001年の2年間分あります。

このとき「たまたま」2000年の6月にビールがよく売れたとします。
3月：400万
4月：450万
5月：500万
6月：1000万
7月：700万
8月：700万
・
・
・
このデータだけ見ると、6月のパラメタは「1000万」と推定したくなりますね。
だからといって「来年も6月にビールが良く売れる」と予測するのはいかがなものでしょうか。

暑い季節にはビールはよく売れるでしょう。
この傾向は続くと予想されます。

しかし、6月によく売れたのは2000年だけかもしれない。
2000年のデータを基にして「6月は売り上げが一気に伸びる」というパラメタを設定すると、少なくとも2000年における予測精度はとても高くなります。
しかし、この傾向が2000年だけのものなのだとしたら、2001年を予測すると、予測精度は落ちるはずです。

そのために2001年は「テストデータ」としてパラメタ推定には使わず、予測精度を評価するために使われるべきなのです。

2．ナイーブな予測との差を評価する

ロサンゼルスはいつも晴れていて、一年のうち98%ほども晴れの日があるそうです。
そんな場所では、下手に難しい計算をしなくても、テキトーに「明日は晴れだよ」といっていたら的中率98%のすごい予測が出来上がりますね。

この例からわかるように「的中率が高いこと」あるいは「予測誤差が少ないこと」は、予測の良さを測るための指標としては不十分です。

では、予測の良さをどのように評価すればよいか。
詳しくは『予測理論とpredictability』で解説してありますが「予測できていないときと比較して、どれだけの差異があるか」を評価することによって、予測の良さを測ります。

問題は「予測ができていない時」をどのように定義するかです。
ここで使われるのが「ナイーブな予測」という考え方です。

「ナイーブな予測」とは、「特別な技術を必要としない単純な予測方法」と考えてもらって構いません。
単純な予測と比べて、どれだけ予測精度が向上したか、という観点で予測を評価するというわけです。

ナイーブな予測としてよく使われるのが以下のようなものです。
1．過去のデータの平均値とする
2．1期前と同じ値とする
3．1年前の同月（同日）と同じ値とする

なお、数量を予測するのではなく分類をする場合なら「常に同じカテゴリを予測値とする（ロサンゼルスで毎日晴れ予報を出すような感じ）」というやり方も候補に入ってくるでしょう。

ここに挙げた3番はデータに周期性がなければ使うことができませんが、1番と2番は汎用的に使うことができます。
Rでもforecastパッケージに予測関数が用意されている（各々『meanf』『rwf』）ので簡単に計算ができます。

 

2．予測誤差の指標

続いて、予測誤差の評価方法に移ります。
ナイーブな予測と自分たちが考案した予測とで各々予測誤差を計算して、それを比較するという流れとなります。

予測誤差はシンプルに

「実際のデータ」 － 「予測値」

から計算ができます。

とはいえ、これはあくまでも1つのデータでの値です。
毎月1回の予測を1年出せば12個のデータが得られますね。この12個において予測誤差を何らかの形で集計しなければなりません。

予測誤差の集計の仕方によって、予測誤差の指標は様々に分かれます。

• ME: Mean Error(平均誤差)
• RMSE: Root Mean Squared Error(平均平方二乗誤差)
• MAE: Mean Absolute Error(平均絶対誤差)
• MPE: Mean Percentage Error(平均誤差率)
• MAPE: Mean Absolute Percentage Error(平均絶対誤差率)
• MASE: Mean Absolute Scaled Error(スケーリングされた平均絶対誤差)
• ACF1: Autocorrelation of errors at lag 1.(誤差の自己相関)
• Theil’s U（タイルのU）

この中でMASEとタイルのUだけわかりにくいので補足しておきます。
MASEは「ナイーブな予測」の予測誤差でスケーリングされた予測誤差です。
デフォルトでは「1期前と同じ値とする」タイプのナイーブな予測が使われています。

タイルのUも同じくナイーブな予測との比較です。
タイルのUが1であれば、ナイーブな予測と同じ予測精度であり、値が小さければ小さいほど、予測精度が高くなっていきます。

これらはすべてforecastパッケージの「accuracy」関数を使うことで計算ができます。

 

3．ナイーブな予測１：ホワイトノイズ

では、ナイーブな予測を実際に計算してみましょう。
まずは「過去のデータの平均値とする」タイプのナイーブ予測です。

その前に、forecastパッケージを読み込みます。
まだインストールされていない方は、Rを右クリックして、管理者として実行してから『install.packages(“forecast”)』を実行してください。

それから『library(forecast)』と実行すれば準備完了です。

ソースコードはこちらから見れます。

シミュレーションデータを作ります。

#----------------------------------------------------------------
# ホワイトノイズのシミュレーション
#----------------------------------------------------------------

set.seed(1)
white_noise <- ts(rnorm(n=450, mean=0, sd=10), start=1)

# 訓練データとテストデータに分ける
train_wn <- window(white_noise, end=400)
test_wn <- window(white_noise, start=401)

450個のデータを作ったうえで、それを訓練データとテストデータに分けました。

なお、このシミュレーションデータは、すべてただの「正規分布に従う独立な乱数」となっています。
これを別名ホワイトノイズと呼びます。

ホワイトノイズのようにデータが右肩上がりや右肩下がりになっていない（トレンドがない）データに対しては、ナイーブな予測として過去の平均値を使うところです。

> # 平均値による予測
> model_wn <- meanf(train_wh, h=50)
> model_wn
    Point Forecast     Lo 80    Hi 80     Lo 95    Hi 95
401      0.3808867 -12.08049 12.84226 -18.70348 19.46525
402      0.3808867 -12.08049 12.84226 -18.70348 19.46525
403      0.3808867 -12.08049 12.84226 -18.70348 19.46525
404      0.3808867 -12.08049 12.84226 -18.70348 19.46525
405      0.3808867 -12.08049 12.84226 -18.70348 19.46525
・・・中略・・・
446      0.3808867 -12.08049 12.84226 -18.70348 19.46525
447      0.3808867 -12.08049 12.84226 -18.70348 19.46525
448      0.3808867 -12.08049 12.84226 -18.70348 19.46525
449      0.3808867 -12.08049 12.84226 -18.70348 19.46525
450      0.3808867 -12.08049 12.84226 -18.70348 19.46525
> mean(train_wh)
[1] 0.3808867

meanf関数にデータを入れるだけです。『h=50』と設定することで「50期先まで予測してください」という指定ができます。
mean(train_wh)の結果と比較すると、予測値であるところの『Point Forecast』はただの平均値となっていることが分かります。
なお、それ以外の『Lo 80』などは予測区間を表しています。『Lo 80』ならば下80%点という意味です。
この予測区間も、時期によらず一定となっていることに注意してください。

予測精度はこちら

> # 予測の精度
> accuracy(model_wn, test_wn)
                        ME      RMSE      MAE      MPE     MAPE      MASE         ACF1 Theil's U
Training set -3.150258e-17  9.683325 7.697074  91.6019 121.3687 0.6781169 -0.046337475        NA
Test set     -1.594355e+00 10.971150 8.807509 112.8624 112.8624 0.7759469  0.005898782 0.9699184

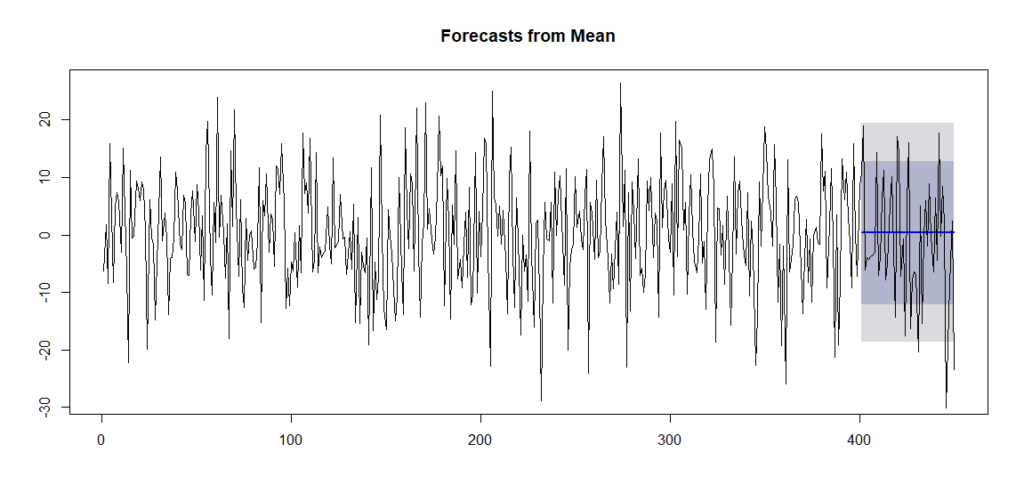
結果をプロットするとこうなります。

# 予測結果のプロット
plot(model_wn)
lines(white_noise)

予測範囲にある程度データが収まっているようです。

 

スポンサードリンク

 

4．ナイーブな予測２：ランダムウォーク

続いて「前期と同じ値を予測値とする」タイプのナイーブな予測を見てみます。
これは、以下のような「正規乱数の累積和」であらわされるようなデータ、別名ランダムウォーク系列に対して適した予測です。

#----------------------------------------------------------------
# ランダムウォークのシミュレーション
#----------------------------------------------------------------

set.seed(8)
random_walk <- ts(cumsum(rnorm(n=450, mean=0, sd=10)), start=1)

# 訓練データとテストデータに分ける
train_rw <- window(random_walk, end=400)
test_rw <- window(random_walk, start=401)

これも同じく、450個のデータを作ったうえで、それを訓練データとテストデータに分けました。

ナイーブ予測モデルを作ります。rwf関数を使います。

> # 前期と同じ値を予測値として使う
> model_rw <- rwf(train_rw,h=50)
> model_rw
    Point Forecast     Lo 80     Hi 80     Lo 95     Hi 95
401         -267.4 -280.5529 -254.2472 -287.5156 -247.2845
402         -267.4 -286.0010 -248.7991 -295.8477 -238.9524
403         -267.4 -290.1814 -244.6186 -302.2412 -232.5589
404         -267.4 -293.7057 -241.0943 -307.6311 -227.1689
405         -267.4 -296.8107 -237.9894 -312.3798 -222.4203
・・・中略・・・
446         -267.4 -356.6070 -178.1931 -403.8303 -130.9698
447         -267.4 -357.5714 -177.2287 -405.3053 -129.4948
448         -267.4 -358.5256 -176.2744 -406.7646 -128.0354
449         -267.4 -359.4700 -175.3301 -408.2089 -126.5912
450         -267.4 -360.4047 -174.3954 -409.6384 -125.1617
> train_rw[400]
[1] -267.4

訓練データの最後のデータ(train_rw[400])が予測値(Point Forecast)として使われていることに注意してください。
また、予測区間が時期を経るごとに幅が広くなっていることが分かります。
「直前の値に、さらにノイズが乗る」ということを想定しているためです。

予測の精度はこちらです。

> # 予測の精度
> accuracy(model_rw, test_rw)
                      ME     RMSE       MAE       MPE     MAPE     MASE        ACF1 Theil's U
Training set  -0.6680556 10.26322  8.201307 -1.825134 15.13502 1.000000 -0.08950607        NA
Test set     -30.5727994 41.84036 35.278951  9.399075 11.27280 4.301626  0.91104384  3.656406

まず、訓練データにおけるMASEが1となっていることに注意してください。
MASEでスケーリングする対象となるナイーブ予測と今回の予測は完全に同じであるため、ここは1になります。
一方、テストデータにおいては「訓練データの最後の値を予測値としたrwf関数の予測値」と「前期と同じ値を予測値とした結果」の比較になるため、rwf関数の長期予測の結果のほうが分が悪くなっています（タイルのUも1を超えています）。

最後に、ランダムウォーク系列に対して、「過去の平均値を予測値として使う」タイプのナイーブな予測を適用するとどうなるか、確認してみます。

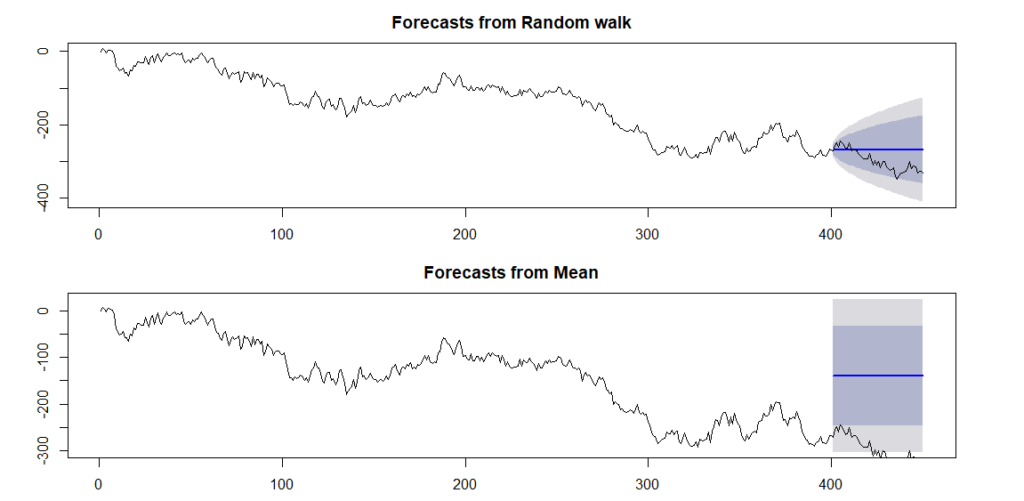
# ランダムウォーク系列には平均値による予測は不適

# 平均値による予測
model_wn_2 <- meanf(train_rw, h=50)

# 2つの予測の比較
par(mfrow=c(2,1), mar=c(2.5,4,2.5,4))

plot(model_rw)
lines(random_walk)

plot(model_wn_2)
lines(random_walk)

par(mfrow=c(1,1))

結果はこちら。

上のグラフが１期間の値を予測値として使ったバージョン、下のグラフが過去平均値を予測値として使ったバージョンです。
下のグラフは、予測区間からデータが大きくはみ出してしまっていることが分かります。

予測精度もやはり１期間の値を予測値として使ったバージョンのほうが精度が高いです。

> # 予測の精度比較
> # １期間の値を予測値として使ったバージョン
> accuracy(model_rw, test_rw)
                      ME     RMSE       MAE       MPE     MAPE     MASE        ACF1 Theil's U
Training set  -0.6680556 10.26322  8.201307 -1.825134 15.13502 1.000000 -0.08950607        NA
Test set     -30.5727994 41.84036 35.278951  9.399075 11.27280 4.301626  0.91104384  3.656406
> # 過去平均値を予測値として使ったバージョン
> accuracy(model_wn_2, test_rw)
                        ME      RMSE       MAE        MPE      MAPE      MASE      ACF1 Theil`s U
Training set -8.502990e-15  82.90064  68.42003 -144.82523 276.51019  8.342576 0.9858850        NA
Test set     -1.588104e+02 161.35878 158.81038   52.84874  52.84874 19.364034 0.9110438   14.7338

今回は「特別な技術を必要としない単純な予測方法」であるナイーブな予測を2パターン示しました。
両者ともに簡単に計算ができるのですが、各々の予測精度については、データによって大きく変わりました。
基本的には、定常過程ならば過去平均値を、非定常過程ならば１期前の値を予測値として使ったバージョンを使うことになります。
定常過程・非定常過程については『ホワイトノイズとランダムウォーク』という記事にも載っています。良ければ参照してください。

予測の比較対象を何にするかでさえある程度まともな奴を選んでやらなくてはなりません。
この上でさらに機械学習などの予測モデルを作って予測を出して、ナイーブな予測と対決させるわけです。

複雑な機械学習のモデルを、ライブラリを使って計算することだけが予測じゃないんだということをご理解頂ければ幸いです。

 

5．意思決定と予測の評価

今回はナイーブな予測と「(accuracy関数から計算される)予測誤差」を比較させることによって、今後作り出す予測モデルを評価しようという趣旨でした。
しかし、もっと良いやり方があります。
それは「予測を実際に使ってみる」ことです。

例えば株式投資に予測モデルを援用したいと思ったとしたならば、実際に「予測モデルを使った株式売買ルール」を定めてやる。
で、その時の収益をシミュレーションすることで予測モデルの評価を行うのです。
もちろん、ナイーブな予測を使った際の株式売買ルールと、収益を比較することは忘れずに。

ここまでやるのは相当の労力を要しますが、予測の評価は、本当はそこまで突っ込んでやった方が良いんですよというお話でした。

 

参考文献

金融データ解析の基礎   金融時系列解析に特化した書籍です。 xtsの使い方やquantmodの使い方に加えて、ARMAやGARCHといった時系列モデルの解説も載っています。

現場ですぐ使える時系列データ分析   R言語を使った時系列分析の方法が書かれた書籍です。 ファイナンスの話題も多く載っています。

Rとトレード ――確率と統計のガイドブック   R言語を用いた証券投資分析の方法が書かれた本です。 Rの基礎から、確率統計の基礎、金融データ分析の基礎、そして株取引のためのプログラミング方法まで幅広く載っている書籍です。 予測を用いた意思決定を実践したい方向けの本です。

書籍以外の参考文献

・Evaluating forecast accuracy
　→forecastパッケージのaccuracy関数に対応する、評価指標の説明が載っています。

スポンサードリンク

更新履歴
2017年7月10日：新規作成
2018年4月24日：タイトルの変更と関連するページのリンクの追加