データ分析入門

2017年7月18日 / 最終更新日時 : 2020年12月27日馬場真哉データ分析入門

t検定の考え方

t検定について、その考え方や計算の仕組みについて説明します。
マニュアルとして手順を覚えるのではなく「なぜその指標を計算するのか」という理由を理解するようにして下さい。マニュアルとして覚えてしまうと、応用がききません。
ExcelやR言語を使ったt検定の実施方法についても併せて理解してください。

なお、ここに書かれていることでわからない用語があれば『記述統計の基礎』を参照するようにしてください。

2018年4月19日追記
拙著「Pythonで学ぶあたらしい統計学の教科書」の発売に合わせて、Pythonでの実行方法を加筆しました。

スポンサードリンク

1．t検定の目的

t検定は、「母平均に対する検定」とも呼ばれます。
平均値を対象とした検定手法なのだということをまずはおさえてください。

平均値に対して「平均値が0と異なるかどうか」を調べたり「リンゴAの大きさの平均値とリンゴBの大きさの平均値が異なるか」といったグループごとの違いを検定したり、といった用途に使われます。

平均値を対象として分析をすることは多くありますので、各々の目的に合わせて検定手法も若干異なってきます。
とはいえ、基本となる考え方は変わらないので、まずは骨子をおさえたうえで、細かな違いに対応できるようにしてください。

以下で、簡単に注意点を説明します。

t検定を使う注意点としては、対象となるデータが「正規分布」という確率分布に従っているという条件を満たす必要があります。
これが満たされていない場合は、一般化線形モデルなどの使用を検討することになります。
この記事では特に触れず、この条件は満たされているのだ、という前提で進めていきます。

この記事では、平均値と期待値の使い分けをしません。すべて平均値で統一します。
期待値と平均値の違いなど、基本的な用語を知りたい方は『記述統計の基礎』を参照してください。

2．t検定の種類

t検定は、その使われ方によっていくつかに分かれてきます。
順番に説明します。

1群のt検定

例えば「データの平均値が0と異なるといえるか」といったことを検定します。
「1組のデータ VS 固定値」の比較だと思えばわかりよいでしょう。

50グラム入りと書かれている製品があったとして「本当に50グラム入っているとみなせるのか」といったことを調べたい場合には、これを使います。
平均値が50グラムと有意に異なっているという結論が出た場合には「書いてあることと違うじゃないか」と文句が言えるわけですね。

対応のあるt検定

「対応のある」とは、例えば「同じ人・物で2回繰り返し計測したときの差を見る」といった場合を指します。

例えば、同じ人を対象として「走る前と走った後で、体温に違いが出るか」といったことを検定するなら「対応のあるt検定」が使われます。

平均値の差の検定:分散が等しい場合・異なる場合

平均値の差の検定とは「同じ学年の男性の身長と女性の身長とで、平均値が異なるか」を調べたり「河口と山の頂で1か月間の気温の平均値が異なるか」を調べたりするのに使われます。
t検定の使い道としては、これが最も多いかもしれません。

なお、2組のデータ（例えば男性の身長と女性の身長など）の間で「データの分散」が異なっていた場合と同じ場合とで、計算の方法が少し変わります。
考え方は同じなのですが。

※2017年8月27日追記
分散が等しい場合であっても「分散が異なることを仮定したt検定」を行っても問題ありません。
むしろ最近は、常に「分散が異なることを仮定したt検定」を行うことのほうが多いようです。

分散が異なるかどうかの検定

分散が異なるかどうかによって、検定の方法が変わるため、あらかじめ「分散が異なるかどうかの検定」をすることがあります。
この検定は「母分散の比の検定」あるいは「F検定」と呼ばれます。
ここで「分散が異なるかどうか」をあらかじめ調べておくことで、最適な手法を選ぶことができます。

もしも、「分散が異なるかどうか」がわからない場合は「分散が異なることを仮定したt検定」をそのまま使うのがセオリーです。
「分散が異なることを仮定したt検定」はWelchのt検定とも呼ばれます。

スポンサードリンク

3．1群のt検定の考え方

まずは、最も簡単な1群のt検定の考え方から見ていきます。
これ以外の検定はすべて、言わば1群のt検定の考え方の応用でしかありません。

有意差が出る条件

1群のt検定では、例えば「このデータの平均値が0と有意に異なるか」といったことを検定します。

検定では「有意差」という言葉がよく使われます。
有意差とは、読んで字のごとく「意味の有る差」のことです。逆に言えば、意味の無い差もありえます。

例えば、平均値が0.0003のデータは「平均値が0と異なる」とみなしてもいいのでしょうか。
なんだか、これほど小さな差であれば「0と異なるとは言えない」とみなしたくもなりますね。
では平均値が0.1の場合はどうなるでしょう？　-1の場合は？
一つ一つ基準を設けるのは大変です。

では、どのような条件を満たせば「このデータの平均値が0と異なるといえる」のでしょうか。
そして「意味の有る差」が得られたとみなせるのでしょうか。

そこで「データの平均値が0と異なるといえる3つの条件」を考えます。

満たすべき条件は以下の3つです。

データの平均値が0と大きく離れている
データの平均値が信用できる（分散が小さい）
サンプルサイズが大きい

順に見ていきます。

条件1:データの平均値が0と大きく離れている

この条件はわかりよいかと思います。
平均値が0.0001である時よりも、326であるときのほうが「0と異なっている」という感じがしますよね。

なので「データの平均値が0と異なるといえる3つの条件」のうちの1つは「データの平均値が0と大きく離れている」ということになります。

条件2:データの平均値が信用できる（分散が小さい）

続いての判断基準は「データがどれだけ信用できるか」です。

たとえば、研究室の中で精密なノギスを用い、0.1mm単位で大きさを測ったとします。リンゴAの大きさの平均値が10cmで、リンゴBの大きさの平均値が11cmでした。
この計測データは信用ができそうです。

一方、10年前に買ったグネグネの定規で大きさを測りました。目盛りが読み取れないので直感で計測したのですが、なんとなくリンゴAの大きさの平均値が10cmで、リンゴBの大きさの平均値が11cmになったような気がしました。
……このデータは、ちょっと信用ができないですね。

この違いはどこにあるのでしょうか。
この違いを数値で表すことができるのが分散です。

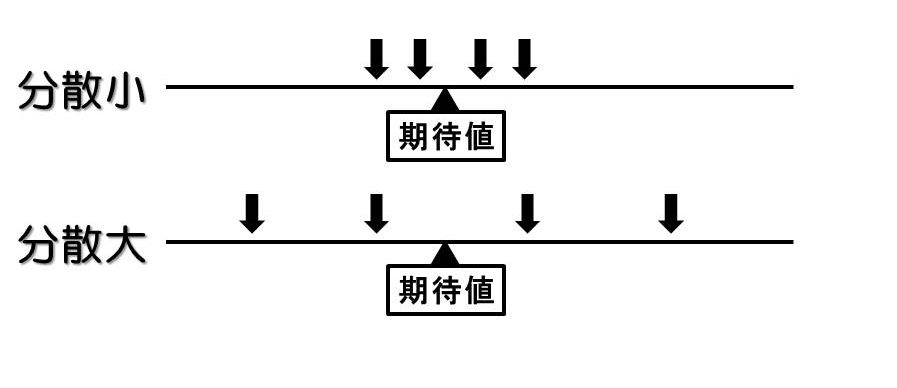
分散とは「データが平均値（期待値）からどれほど離れているか」を表した指標です。
データと、平均値との距離だとみなすこともできます。

上の図を見てもらえればわかるように、分散が小さければ、データは平均値の近くに集まっています。分散が大きければその逆です。
今から「平均値」を対象として分析をするのでした。
それなのに「データが平均値から遠く離れている」のであれば、その平均値をあまり信用することができませんね。

精密に測れば、分散が小さくなるので、たとえ平均値の差が小さかったとしても「意味の有る差」だとみなすことができます。すなわち、有意差が出ます。
同じ平均値でも、分散の大きい小さいによって、結果が変わるのだということをご理解ください。

なお、分散は偏りをなくすために「不偏分散」というものを使うのが普通です。
普通の分散(標本分散とも言います)と不偏分散の違いを知りたい方は『記述統計の基礎｜不偏分散』を参照してください。
以下、分散と書けば不偏分散を指していると考えてください。

条件3:サンプルサイズが大きい

一回の調査（サンプリング）で得られたデータの個数を、サンプルサイズと言います。
サンプルサイズは大きければ大きい方が「有意差」が出やすいです。

これは「袋菓子を1つだけ開けたら、48グラムだった。封入量が50グラムよりも少ない！」というようなクレームをつけてはいけない、というところから想像がつくかと思います。
1つだけしか調べていないと「たまたま」「偶然」そうなっただけという可能性を排除できないんですね。
2個目の袋を開けたら52グラムで、平均したら50グラムになっていた、なんてこともあるでしょう。

サンプルサイズが小さければ、偶然の要素が大きくなります。一見差があるように思えても、意味の有る差とは言えないこともしばしばです。
サンプルサイズが大きければ、偶然の要素が小さくなります。なので、意味の有る差だとみなしやすく、有意差が出るのです。
平均値も分散も同じ値だったとしても、サンプルサイズの大小によって、有意か有意でないかが変わることがあります。

t値

今まで「データの平均値が0と異なるといえる3つの条件」を見てきました。
再掲します。

データの平均値が0と大きく離れている
データの平均値が信用できる（分散が小さい）
サンプルサイズが大きい

あとはこの3つの条件を数値で表すことができれば、ひとまずのゴールです。
この「3つの条件を数値で表したもの」をt値と呼びます。

$$t値=\frac{平均値の差}{\sqrt[]{分散\divサンプルサイズ}}$$

このt値が大きければ、先の3条件のすべてが満たされていることを確認してください。

分散はσ²、サンプルサイズはnであらわすのが普通です。
また平均値をμとすると、以下のようになります。

$$t値=\frac{\mu – 0}{\sqrt[]{\sigma^2 \div n}} = \frac{\mu – 0}{\sigma / \sqrt[]{n}}$$

もしも、平均値が50と異なるかどうかを見たいのであれば、以下のようになります。

$$t値(平均値が50と異なるか)= \frac{\mu – 50}{\sigma / \sqrt[]{n}}$$

t値とp値

t値が大きければ「平均値に有意な差がありそうだ」とみなすことができることがわかりました。
次の問題は「t値がいくらになれば『大きい』と判断できるか」という基準を定めることです。

3を超えれば大きいとみなせるのか、4を超えなきゃダメなのか、難しいところです。
そこで、「統計的仮説検定」という枠組みが使われるわけです。

t値を計算すると、p値と呼ばれる値に変換できます。
変換です。
t値がわかっていれば、p値には（パソコンを使って計算すれば）すぐに変換できます。
t値が大きくなれば、p値は小さくなります。
そして、p値は基準が定まっています。p値は0.05を下回れば小さいとみなす、と伝統的に決まっています。

というわけで、

t値をp値に変換する
t値が大きければ、p値は小さくなる
p値が0.05を下回るくらい小さければ、t値は十分大きいといえる

上記の3ステップを踏むことで、t値の大小判定ができます。

この変換は、Excelなどを使えば簡単に計算できます。
後ほど詳細を説明します。

p値を解釈する

データを分析する際にとても怖いのが「たまたまそうなった」という「たまたま」あるいは「偶然」です。
「たまたま」袋菓子に入っているお菓子の量が少なかったとか、「たまたま」うっかり重量計の目盛りを見間違えてしまったとか、そんなデータでテストをしていた可能性もなくはないわけです。
こんなデータを使うと、「たまたま」袋菓子の量が50グラムを下回っているように見えてしまい、t値も大きくなってしまうでしょう。
そんな「たまたま、t値が大きくなって、差があるように見えてしまう確率」がp値です。

少々荒い定義ですが、p値とは「たまたま、t値が○○よりも大きくなる確率」であると覚えておくとよろしいかと思います。
例えばt値が2でp値が0.06だったとしたら「たまたま、t値が2よりも大きくなる確率は6%です」というように解釈します。

補足：帰無仮説・対立仮説

ここからは、統計学の専門用語の解説となります。
実務に使う際ならば、上述の知識で何とかなりますので、難しければ飛ばしてください。

今回の場合は、以下のようになります。

帰無仮説：データの平均値は0である
対立仮説：データの平均値は0と異なる

対立仮説は「私たちが立証したい仮説」のことです。
帰無仮説はその逆だと思えばわかりよいです。

補足：検定の非対称性

なぜ帰無仮説というものをいちいち置くのかというと、その原因が検定の非対称性にあります。

検定は「帰無仮説が異なっている」ということの立証はできます。
p値が0.05以下になれば、帰無仮説が異なっているとみなすわけです。

でも「仮説が正しい」と主張することはできません。違うことが言えるだけです。
これを検定の非対称性と呼びます。

なので、「p値が0.05より大きかったので、帰無仮説が間違っているといえなかった」からといって「帰無仮説は正しい」とはならないことに注意してください。

違っていることの立証はできますが、正しいことの立証はできません。
それが統計的仮説検定です。

まとめ

検定の流れをもう一度まとめます。

有意差が出るには3つの条件がある

平均値の差が大きい
データが信用できる（分散が小さい）
サンプルサイズが大きい

↓
この3つの条件を勘案したのがt値である
↓
t値が大きければ、先の3条件を満たしたといえる
↓
t値はp値に変換できる
↓
p値とは「たまたま、t値が大きくなって、差があるように見えてしまう確率」のことである
↓
p値が0.05を下回れば、（偶然である可能性が小さいから）t値は十分大きいとみなせる

p値＜0.05で「有意差あり」
p値が0.05より大きければ「有意な差があるとは言えない」と判断する

特にt値の意味については、ぜひ自分で解釈ができるようになっておいてください。

4．p値の計算とその解釈

検定をするとp値というのが計算できて、それが小さければ有意になるというところまで説明しました。
しかし、どのようにしてp値に変換するのでしょうか。

その時に使われるのが確率分布という考え方です。

確率分布について知りたい方は『確率分布と確率変数の基礎』と『確率密度関数と正規分布』を参照してください。

もしも確率分布がわかっていなかったならば、p値を求めるためには「同じ調査を100万回行って、その時にt値がどんな値をとるかを調べる」必要があります。
例えば100万回のうち6万回t値が2を上回ったのであれば、p値＝6万÷100万＝0.06と計算ができますね。
ですが、これだけの回数をまともに調査を繰り返すのは不可能です。
そこで、計算をしてp値を求めます。

もしも元のデータが「正規分布」という確率分布に従っているのだとしたら、t値は「t分布」という確率分布に従うことがわかっています。正規分布もt分布も（ちょっとややこしいですが）計算式であらわすことができるものです。パソコンを使えば瞬時に確率が計算できます。
なので、t分布という確率分布を使えば、p値をすぐに計算することができます。

逆に言えば、元のデータが正規分布に従っていなかった場合には、正しくp値を計算することができません。
注意してください。

5．対応のあるt検定の考え方

対応のあるt検定は、1群のt検定と考え方がほとんど変わりません。
データの集計の方法が変わるだけです。

というわけで、対応がある場合のデータの集計方法を見ていきましょう。

テレビゲームって面白いですよね。体は動かさないですが頭は使います。
そこで、被験者に、ゲームをする前とゲームをした後で体温を測定してもらいました。
テレビゲームで体温が上がるのか、検定してみます（架空の実験データです）。

対応のあるt検定

被験者	ゲーム前	ゲームの後	差分
山田さん	36.2	36.2	0.0
佐藤さん	36.9	36.5	-0.4
田中さん	35.3	36.3	1.0
鈴木さん	36.4	37.1	0.7
加藤さん	36.0	36.7	0.7

一番右の列「差分」列を見てください。
これは「ゲーム前 – ゲーム後」の体温の差をとったものです。

もしも、ゲーム前後で体温が変わらないのだとしたら、この差分は0になるはずですね。
というわけで「差分データの平均値が0と異なるかどうか」を検定すれば、「ゲーム前後で体温が変わるか」を検定できることになるのです。

差をとってから、1群のt検定を行うのが「対応のあるt検定」だということです。

6．平均値の差の検定の考え方

2群のデータにおける平均値の差の検定をする場合でも、基本的な考え方は1群のt検定と同じです。
ただし、データが増えるので、計算方法が若干変わってきます。

有意差の出る3条件を再掲します。

平均値の差が大きい
データが信用できる（分散が小さい）
サンプルサイズが大きい

難しいのは「分散」の計算方法です。
データが2群に分かれると、これを計算するのが難しくなります。
また、2群が同じ分散であればよいのですが、分散の大きさが異なるとなれば、さらに計算が複雑になります。

逆にいれば、分散の計算が難しくなったということを除けは、考え方に違いはまったくありません。

補足:t値の計算方法（等分散の場合）

ここからはおまけです。
数式が出てくるうえ、こういった込み入った計算はすべてパソコンがやってくれるので、人間が手で計算するようなことには普通なりません。
理解ができなくても先に進んでもらって結構です。

まずは、等分散の場合のt値の計算方法を見ていきます。

2群のデータをXとYと呼ぶことにします。
種類の違うリンゴなのだと思ってもらって結構です。
これの大きさを各々計測しました。

各々の種類の大きさの平均値を、Xバー（Xの上に横線）、Yバー（Yの上に横線）と記すことにします。
Xのサンプルサイズはm、Yのサンプルサイズはn個です。
また2群を合わせた分散をs²とします。

$$s^2(2群を合わせた分散)= \frac{ (\sum_{ i = 1 }^{ m } X_i – \overline{ X })^2 + (\sum_{ j = 1 }^{ n } Y_j – \overline{ Y })^2 }{m + n – 2}$$

これを使ってt値を計算します。

$$t値(2群・等分散)= \frac{ \overline{ X } – \overline{ Y }}{s \sqrt[]{ \frac{1}{m} + \frac{1}{n}} }$$

t値の概念式との関係を確認してください。

$$t値=\frac{平均値の差}{\sqrt[]{分散\divサンプルサイズ}}$$

参考までに「普通の（1群の）」不偏分散とt値は以下のように計算されます。

$$不偏分散(1群) :\sigma^2 = \frac{ \sum_{i=1}^{m}(X_i – \overline{ X })^2 }{m-1}$$

$$t値(平均値が50と異なるか) = \frac{\overline{ X } – 50}{\sigma \sqrt[]{\frac{1}{m}}}$$

補足:t値の計算方法（分散が異なる場合）

次は分散が異なる場合のt値の計算方法を説明します。
むしろこちらのほうが直感的かもしれません。

先ほどと同じように、2群のデータをXとYと呼ぶことにします。
Xの不偏分散をs_x²、Yの不偏分散をs_y²とします。

$$不偏分散(X): s_{x}^2 = \frac{ \sum_{i=1}^{m}(X_i – \overline{ X })^2 }{m-1}$$

$$不偏分散(Y): s_{y}^2 = \frac{ \sum_{j=1}^{n}(Y_j – \overline{ Y })^2 }{n-1}$$

t値は、各々の不偏分散をそのまま使う格好になります。

$$t値(2群・不等分散)= \frac{ \overline{ X } – \overline{ Y }}{\sqrt[]{ s_{x}^2 / m + s_{y}^2 / n} }$$

補足
この場合は、t分布の自由度の計算方法が大きく変わります。
不等分散でのt検定はウェルチの検定とも呼ばれます。

補足:等分散性の検定

分散が異なるかどうかを検定する場合はF検定と呼ばれる手法を使います。
F検定も、データが正規分布に従っていることを前提とした検定ですので、注意してください。

F検定ではF比と呼ばれる値を計算します。

先ほどと同じように、2群のデータをXとYと呼ぶことにします。
Xの不偏分散をs_x²、Yの不偏分散をs_y²とします。

$$不偏分散(X): s_{x}^2 = \frac{ \sum_{i=1}^{m}(X_i – \overline{ X })^2 }{m-1}$$

$$不偏分散(Y): s_{y}^2 = \frac{ \sum_{j=1}^{n}(Y_j – \overline{ Y })^2 }{n-1}$$

F比は、両者の比をとったものです。

$$F比 = s_{x}^2 / s_{y}^2$$

この比が1から離れていれば、分散が異なるということはすぐわかるかと思います。

F比→p値への変換についてはF分布という確率分布を使います。

7．Excelによるt検定

t検定計算ファイルを作りました。
なお、Excel2010以上で動きます。これより古いExcelをお使いの方は、関数からドット（.）を取り除いてください。
t-test.xlsx

t値→p値への変換は『T.DIST』関数を使います。
1群のt検定のみ、関数が用意されていないようでしたので、これを使いました。

ほかの検定は、軒並み、検定用の関数が用意されています。
この関数はとても便利でして、t値をわざわざ求めなくても、p値を即座に計算してくれます。
しかし、それでは勉強にならないので、リンクを張ったExcelサンプルシートでは、t値も別途計算しています。

対応のあるt検定は以下のように指定します。

=T.TEST(データX,データY,2,1)

設定例
=T.TEST(D5:D12,E5:E12,2,1)

最初の2つの引数はデータです。
3つ目の引数が片側検定か両側検定かを指定する部分です。
普通は何も考えずに『２（両側検定）』を指定します。

専門用語が出てきたので解説します。
片側検定とは「XがYよりも小さいかどうかを検定する」といったように、方向性があります。
この場合だと「XがYより大きいということはあり得ないので、最初から考えない」ということになります。
しかし、そんな前提を置くことはふつうしません。
「XがYと異なるかどうか検定する」場合には、XがYより大きかろうが小さかろうが気にしませんね。「違う」ことだけが重要ですので。
その場合は両側検定を使います。
繰り返しになりますが、普通は何も考えずに『２（両側検定）』を指定します。
なお、あとで説明するR言語は、何も指定しなければ勝手に両側検定となります。

4つ目の引数が検定のタイプです。
1：対→対応のあるt検定
2：等分散の2標本
3：非等分散の2標本

これを変えれば、他の検定も実行ができます。

分散の比の検定ではF.TESTという関数を使います。
これはデータを指定するだけで行けます。

=F.TEST(データX,データY)

設定例
=F.TEST(D5:D12,E5:E12)

8．R言語によるt検定

R言語だと、プログラムを書かなければなりませんが、平均値や分散などを一発で全部出力しれくれるので、レポートなどを書く際にはこちらのほうが楽という説もあります。
R言語をまだ触ったことがないという方は『Rの簡単な使い方』を参照してください。
プログラムは数行しか書かないので、それほどは難しくないです。

まずはデータを用意します。

# データ
data <- data.frame(
  X = c(2, 0, 3, -3, 4, 1, -1, 4),
  Y = c(5, -1, 2, -1, 7, 3, 4, 5)
)

こんなデータになっています。

> # データの中身
> data
   X  Y
1  2  5
2  0 -1
3  3  2
4 -3 -1
5  4  7
6  1  3
7 -1  4
8  4  5

今回は手作業でデータを作りましたが、Excelなどから読み込むこともできます。
別のサイト様ですが『統計解析フリーソフト R の備忘録頁｜EXCEL のデータを読み込む』あたりを読まれると良いかと思います。
本筋とは関係ないですが、このサイト様はかなり内容が充実しているので、これを読めばR言語は大体使えるようになります。

まずは1群のt検定です。
『t.test』関数を使います。t検定は全部これを使います。

> # 1群の検定
> t.test(data$X)

	One Sample t-test

data:  data$X
t = 1.4183, df = 7, p-value = 0.1991
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.8340722  3.3340722
sample estimates:
mean of x 
     1.25

『t.test』の引数にデータを入れるだけです。『data$X』で、Xのデータだけを取り出していることに注意してください。

次は対応のあるt検定です。
2つのデータを入れたうえで『paired=T』と指定します。
『p-value = 0.0467』となっているので、有意差ありです。

> # 対応のあるt検定
> t.test(data$X, data$Y, paired=T)

	Paired t-test

data:  data$X and data$Y
t = -2.4111, df = 7, p-value = 0.0467
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -3.4662444 -0.0337556
sample estimates:
mean of the differences 
                  -1.75

次は、分散の比の検定です。
var.testという関数を使います。

> # 母分散の比の検定
> var.test(data$X, data$Y)

	F test to compare two variances

data:  data$X and data$Y
F = 0.75, num df = 7, denom df = 7, p-value = 0.7139
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.1501529 3.7461819
sample estimates:
ratio of variances 
              0.75

『p-value = 0.7139』ですので、分散が異なるとは言えないという結果になりました。
なので、基本的には等分散の2標本t検定だけをやればいいのですが、勉強のために両方やっておきます。

等分散の2標本t検定です。
『var.equal = T』と指定することに注意してください。

> # 等分散の場合の平均値の差の検定
> t.test(data$X, data$Y, var.equal = T)

	Two Sample t-test

data:  data$X and data$Y
t = -1.2999, df = 14, p-value = 0.2146
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -4.637507  1.137507
sample estimates:
mean of x mean of y 
     1.25      3.00

p値>0.05ですので「有意な差があるとは言えない」という結果です。対応のあるt検定では有意差ありだったのですが、こちらはだめでした。
基本的に、対応のあるt検定のほうが有意差が出やすいということは覚えておくとよろしいかと思います。

最後は分散が異なる場合のt検定です。『var.equal = F』とします。

> # 不等分散の場合の平均値の差の検定
> t.test(data$X, data$Y, var.equal = F)

	Welch Two Sample t-test

data:  data$X and data$Y
t = -1.2999, df = 13.72, p-value = 0.2151
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -4.643046  1.143046
sample estimates:
mean of x mean of y 
     1.25      3.00

Excelの結果と一致していることを確認してください。

9．Pythonによるt検定

人気のプログラミング言語であるPythonを使っても、簡単にt検定を実行することができます。
Pythonをまだ触ったことがないという方は『Pythonの簡単な使い方』を参照してください。

Jupyter Notebookの使用を前提とします。実行結果をまとめたものは『t-test.html』から参照することができます。レポートのように簡単に結果を残せるのはJupyter Notebookの利点です。

まずは必要なライブラリのインポートを行います。
実はnumpyなどの使わないのも入ってるんですが、これらは分析においてしばしば必要となるので、一括でインポートしておくと便利です。
表示桁数の指定もしておきました。

# 必要なライブラリのインポート
import numpy as np
import pandas as pd
import scipy as sp
from scipy import stats

# 表示桁数の指定
%precision 3

データを用意します。pandasのDataFrameという形式とします。

# データを用意する
data = pd.DataFrame({
  "X": [2, 0, 3, -3, 4, 1, -1, 4],
  "Y": [5, -1, 2, -1, 7, 3, 4, 5]
})

print(data)

こんな結果になっています。

まずは1群のt検定です。
scipy.statsのttest_1samp関数を使います。基本的な検定はscipy.statsを使えば済むことが多いです。
ttest_1samp関数の引数は、対象となるデータと、帰無仮説で仮定している平均値の値の2つです。
細かいんですが、ドット（.）記号を使うことで特定の列を抽出しました。

# 1標本のt検定
stats.ttest_1samp(data.X, 0)

以下のような結果が出てきます。四捨五入すればExcelやRと同じ結果ですね。

Ttest_1sampResult(statistic=1.4182715723279384, pvalue=0.19905953953787844)

次は対応のあるt検定です。
2つのデータを入れたうえでttest_rel関数を実行しました。

# 対応のあるt検定
stats.ttest_rel(data.X, data.Y)

以下のような結果になります。
Ttest_relResult(statistic=-2.4111323733951022, pvalue=0.046696268859509782)

最後に、対応の無いt検定です。ttest_ind関数を使います。
まずは分散が等しい場合です。『equal_var=True』と指定します。

# 分散が等しいことを仮定したt検定
stats.ttest_ind(data.X, data.Y, equal_var=True)

結果はこちら。
Ttest_indResult(statistic=-1.299867367239363, pvalue=0.21464181738984914)

分散が異なることを仮定したWelchの方法を実行します。『equal_var=False』とします。

# 分散が異なることを仮定したt検定（Welchの方法）
stats.ttest_ind(data.X, data.Y, equal_var=False)

結果はこちら。
Ttest_indResult(statistic=-1.299867367239363, pvalue=0.21506175265308078)

Jupyter Notebookを使うと、手軽に分析を実行することができます。
統計分析といえばR言語というイメージがあるかもしれませんが、実行速度はPythonの方が早いこともしばしばあります。
Pythonも併用して学ばれるとよろしいかと思います。

今回は「統計的仮説検定」に絞って解説をしていきました。
検定は便利なのですが、使える範囲が絞られてきます（検定の非対称性があるので「仮説が正しい」と主張することができないのはなかなかやりにくいものです）。
もっと、広く柔軟にデータを分析する方法として「統計モデル」という考え方が普及しています。
特に一般化線形モデルは文献も多く、RやPythonを使えば簡単に計算ができます。

統計学において、何をどこまで学ぶのかは、個人の意思が尊重されるべきだと思います。
しかし、もしも統計学を深く学んでみたいという方がこの記事を読まれていたら、ぜひ「統計的仮説検定のその次」へ進んでいただければと思います。
キーワードは統計モデル、そして一般化線形モデルです。この辺がわかれば、また次の技術へ移っていくこともできるでしょう。
より発展的な話題としてベイズ統計学も挙げられます。
詳しくは、下で挙げた参考文献を読んでみてください。

参考文献

Pythonで学ぶあたらしい統計学の教科書

このサイトの管理人が書いた本です。
確率変数・確率分布や、数量データ・カテゴリデータの違いといった基本から、統計モデル・機械学習といった応用まで学びます。
紹介ページはこちら。
出版社サイトはこちら。

統計学入門 (基礎統計学)

かなり内容の濃い、言い方を変えると難しい本ですが、是非一度読まれることをお勧めします。
20年間売れ続けている、統計学のロングセラーです。
この本が読めれば、統計学の基礎は大体OKです。

マンガでわかる統計学入門

統計学の漫画本はいくつかありますが、こちらの本は、やや内容が多く、本格的です。
t検定についても載っています。
上で挙げた、ちょっと難しい統計学入門書の副読本として使いやすい構成になっています。

データ解析のための統計モデリング入門――
一般化線形モデル・階層ベイズモデル・MCMC

統計的仮説検定の「次」に行きたい方にお勧めする、新しい統計学の入門書です。
統計学について、より突っ込んで学んでみたい方にお勧めします。

平均・分散から始める一般化線形モデル入門

このサイトの管理人が書いた本です。
平均や分散といった基本から、一般化線形モデルまで解説しています。
この記事は第1部「統計学の基礎と検定の考え方」を大幅に加筆修正して作成されたものです。
サポートページはこちら。

「平均・分散から始める一般化線形モデル入門」を購入されるときの注意
定価は2500円(税抜き)ですが、Amazonさんなどでは在庫が不足しており、中古価格が高騰していることがあります。
重版したので出版社には在庫が残っています。出版社のサイトからですと送料無料・書籍代は後払い・最短翌日出荷で、確実に定価で手に入ります。
以下のネット書店も併せてご利用ください。

スポンサードリンク