記述統計の基礎

本格的に確率・統計を学ぶ前に、まずは基礎体力をつけます。

ここでは、記述統計と呼ばれる「データの集計方法を学ぶ学問」について説明します。
この記事を読めば、平均値と期待値の違い、分散や普遍分散、標準偏差、標準誤差の意味が理解できるはずです。
どのようにしてデータを集計するのか、そして、なぜデータの集計が必要なのかを理解してから次のステップに移ってください。

スポンサードリンク

目次

1. 記述統計と推測統計
2. なぜ記述統計が必要か
3. データの種類
4. 度数分布
5. 期待値と平均値
6. 期待値の数理、平均値の数理
7. 分散
8. 分散の数理
9. 不偏分散
10. 標準偏差
11. 標準誤差
12. 期待値の標準偏差としての標準誤差
13. 参考文献

 

1．記述統計と推測統計

統計学は、記述統計と推測統計に分かれます。

記述統計学とは「手持ちのデータを集計する方法を学ぶ学問」です。
推測統計学とは「手持ちのデータを分析して、まだ手に入れていないデータについて議論する方法を学ぶ学問」です。

推測統計学こそが、統計学において最も重要な部分です。
記述統計学は、推測統計学の前処理に当たるものだと考えてもらって構いません。
記述統計を学ぶ必要はありますが、記述統計だけでは、データを社会の役に立たせることはできないということです。
これから統計学を学ぶ方は、推測統計学まで学ばれることを強くお勧めします。

当サイトでは、特に断りがない限り、統計学と書けば、それは推測統計学を指します

 

2．なぜ記述統計が必要か

記述統計だけでは、データを社会の役に立たせることはできません。
しかし、記述統計無しで推測統計を学ぶこともできません。

推測統計は「手持ちのデータを分析して、まだ手に入れていないデータについて議論する方法を学ぶ学問」です。
そして、統計的予測理論においては「未来は過去と同じ」という前提を置いて予測を行います。

以下の2つの予測を比較してください。
①「気温が高いとビールが売れるというコトが1回だけあった」だから「今後、気温が高いとビールが良く売れる」
②「気温が高いとビールが売れるというコトが5万回もあった」だから「今後、気温が高いとビールが良く売れる」

どちらの予測のほうが信用できますか。
当然②でしょう。多くのデータを使って予測したほうが信用できます。

データが多いほうがよさそうというのは多くの方が想像できるかと思います。
ただ、多くのデータを、一つ一つ分けて扱うのは面倒です。

例えば、以下のようなデータがあったとしましょう。
データ①｛1,3,5,10｝
データ②｛6,7,8,9 ｝

どちらの方が大きそうですか？ 最小の値は 1 で、それはデータ①に含まれています。だから①の方が小さい？
最大の値は 10 で、それはデータ①に含まれています。だから①の方が大きい？
比較の仕方はたくさんあります。全部試すのは誠実なやり方かもしれませんが、面倒です。

そこで、データを集計します。
データを集計することによって、たくさんのデータを使っているのにかかわらず、少数の集計値のみを対象として分析を進めることができるようになります。
便利です。

なお、一回の調査（サンプリング）で得られたデータの個数を、サンプルサイズと言います。
電子顕微鏡でリンゴの大きさを10個測ればサンプルサイズ10です。
15人にアンケートを取れば、サンプルサイズ15です。
データを比較するときは、データの数も重要な要素となります。

 

3．データの種類

データの集計値を求めると一口に言っても、データの種類によってまとめ方は大きく異なります。
まずは、データの種類について説明します。

データの種類は大きく分けて2つあります。
数値か、数値でないかの2つです。

数値のデータは「数量データ」と呼ばれます。
数値じゃないデータは「カテゴリデータ」と呼ばれます。

数値のデータ、すなわち数量データには、例えば、以下のようなものがあります。
身長、体重、金額、魚の尾数、商品の個数、気温

数値じゃないデータ、すなわちカテゴリデータには、以下のようなものがあります。
性別、魚の種類、天気（晴れや雨）

数量データをカテゴリデータにすることも可能です。
例えば、身長だと、以下のようにしてカテゴリデータに変換できます。
100㎝～120㎝：カテゴリA
120㎝～140㎝：カテゴリB
140㎝～160㎝：カテゴリC
160㎝～180㎝：カテゴリD
180㎝～200㎝：カテゴリE

この変換はあとで使うので覚えておいてください。

なお、この記述統計の記事においては、断りがない限り、データは「数量データ」だとみなして話を進めていきます。

 

4．度数分布

度数分布とは、「同じものがいくつあるのか」をまとめたものです。

カテゴリデータの場合は簡単に求められます。
猫が10匹いました。
うち4匹がオスで、6匹がメスでした。
度数分布は、「オス：4匹、メス：6匹」となります。

身長などの数量データの場合は、いったんカテゴリデータに戻してから度数分布を求めるのが普通です。
例えば、以下のように数量データをカテゴリデータに変換します。
100㎝～120㎝：カテゴリA
120㎝～140㎝：カテゴリB
140㎝～160㎝：カテゴリC
160㎝～180㎝：カテゴリD
180㎝～200㎝：カテゴリE
で、カテゴリAが4人、Bが7人……と求めていきます。
これが度数分布です。

 

5．期待値と平均値

期待値とは、比較する対象です。
データを手に入れたとき、そこには数値がたくさんあると思います。その数値を全部そのまま扱おうとすると大変です。
たくさんのデータを要約した値を使ったほうが楽です。
その要約した値こそが期待値です。
期待値は平均値と大体同じです。その違いについては次の節で解説します。

期待値の特徴を説明します。
(1) 期待値は、各々の値が大きければ大きいほど大きくなります。
(2) ただし、「大きな値」があっても、その「大きな値」が生じにくければ、期待値はあまり大きくなりません。
気温の例でいえば、(1)により、暑い日があれば気温の期待値も大きくなることがわかります。しかし、(2)により、100日中暑い日がたった1日しかないということであれば、気温の期待値はあまり高くなりません。

大阪の気温が10個、東京の気温が10個あったとき、どちらのほうが暑いか、ということを調べようと思ったら、各々の気温の期待値を取って比較すればいいわけです。例えば、大阪の気温の期待値が30度で、東京の気温の期待値が25度だったとします。そしたら「大阪の方が暑い」と一瞬でわかります。少なくとも20個のデータを全部見るよりかは楽です。

「データを比較する」という行為を、これからは「期待値(平均値)の大小を比較する」という言葉に置き換えることができます。
そうすれば比較がとても簡単になります。
期待値って便利ですね。

 

6．期待値の数理、平均値の数理

期待値は平均値と大体一緒ですが、意味合いが少し違います。期待値と平均値の使い方の違いについても理解してください。

期待値は以下の式で計算されます。p_iはあるデータが生じる確率、x_iがそのデータの値、nがサンプルサイズです。

$$\sum_{i=1}^{n} p_ix_i$$

↑の式は言い換えるとこうなります。

 期待値＝『確率×その時の値』の合計

例を挙げます。

データが、｛19が二つ、20が五つ、21が三つ｝だとしたら、データの個数は合計10個より、
19になる確率　＝　2÷10
20になる確率　＝　5÷10
21になる確率　＝　3÷10
よって期待値は以下のように計算されます。

$$19\times{\frac{2}{10}}+20\times{\frac{5}{10}}+21\times{\frac{3}{10}}=20.1$$

記号の読み方を説明します。
pが確率で、p_iと添え字「i」がついたものは、先ほどの例でいうと
p₁= 「19になる確率」      （　＝　2÷10）
p₂= 「20になる確率」      （　＝　5÷10）
p₃= 「21になる確率」      （　＝　3÷10）
です。

x_iは先ほどの例において、以下のようになります。
x₁  = 19
x₂  = 20
x₃  = 21

期待値の特徴を復習します。

1. 期待値は、各々の値(例においては19とか21とかいう数値)が大きければ大きいほど大きくなります。
2. ただし、「大きな値」があっても、その「大きな値」が生じにくければ(確率p_iが小さければ)、期待値はあまり大きくなりません。

続いて平均値の定義を式で書きます。xがデータの値、nがサンプルサイズです。

$$\frac{1}{n}\sum_{i=1}^{n}x_i$$

データが、｛19が二つ、20が五つ、21が三つ｝だとしたら、平均値は以下のように計算されます。

$$\frac{19+19+20+20+20+20+20+21+21+21}{10}=20.1$$

期待値との違いを理解してください。
端的に言うと
・1/n
・p_i
どちらを使うかというだけの話です。
｛19が二つ、20が五つ、21が三つ｝という例では、期待値も平均値も両方とも同じ値になります。
期待値と平均値は大体一緒です。

しかし、期待値の方が平均値よりも応用範囲が広いです。
例を挙げます。
あなたが株をやっていて、2020年5月1日に儲けることのできる金額を予想したいと思ったとしましょう。
株価が暴落すれば100万円損します。
暴落しなければ5万円儲かります。
さて、この時、期待値を「想像すること」は簡単です。
・株価が暴落する確率を5% (5/100)
・暴落しない確率を95% (95/100)
と仮に予想できれば、期待値は

$$-100\times\frac{5}{100}+5\times\frac{95}{100}$$

で計算できそうです。

では、2020年5月1日にあなたが儲けることのできる平均値はいくらになるでしょうか。
平均値を計算するためには一つ一つのデータが必要です。
2020年5月1日という日がたくさん必要になるのです。
2020年5月1日に儲ける金額の平均値は以下のようにして求められます。
・2020年5月1日という日が100日存在する
・100日ある2020年5月1日という日において、5日だけ暴落する。
・100日ある2020年5月1日という日において、95日は暴落しない。
ゆえに平均値は、以下で求まります。

$$\frac{-100-100-100-100-100+5+5+…+5}{100}$$

…のところは5が95個入ると思ってください。
これで期待値と同じ結果が導けます。

さて、期待値と平均値、使いやすいのはどちらですか？
きっと、期待値の方が状況を理解しやすいことと思います。
期待値は、「平均値をいろいろな状況で想像することができるように拡張したもの」だと思えばわかりよいでしょう。

これから先、個数を想像できない場面に出くわすことは多々あります。2020年5月1日という日が100日あることが想像できないのと同様に。
そんな時、平均値が計算できなくておしまい、では困ります。でも、期待値ならば、計算できます。想像できます。期待値ってすごいんです。
データの代表値としては、ぜひ期待値を使ってください。平均値との違いについて、ご納得いただければ幸いです。

スポンサードリンク

 

7．分散

分散は「データが期待値からどれほど離れているか」を表す指標です。
期待値は便利だと説明しました。比較が楽になるからです。
しかし、期待値を比較するだけではうまくいかない場合があります。

たとえば、電子顕微鏡を用い、0.001mm単位で大きさを測ったとします。リンゴAの大きさの期待値が10cmで、リンゴBの大きさの期待値が11cmでした。
一方、5年前に買った折れ曲がった定規で大きさを測りました。曲がっているので測るたびに値が変わるのですが、なんとなくリンゴAの大きさの期待値が10cmで、リンゴBの大きさの期待値が11cmになったような気がしました。
さて問題。リンゴの大きさの期待値の比較が「できる」のはどちらで「できない」のはどちらですか。

電子顕微鏡を使った結果を用いて比較するのはOKです。
でも、曲がった定規で測った結果で比較するのは普通ダメです。
この違いはどこにあるのでしょうか。
この違いを数値で表すことができるのが分散です。

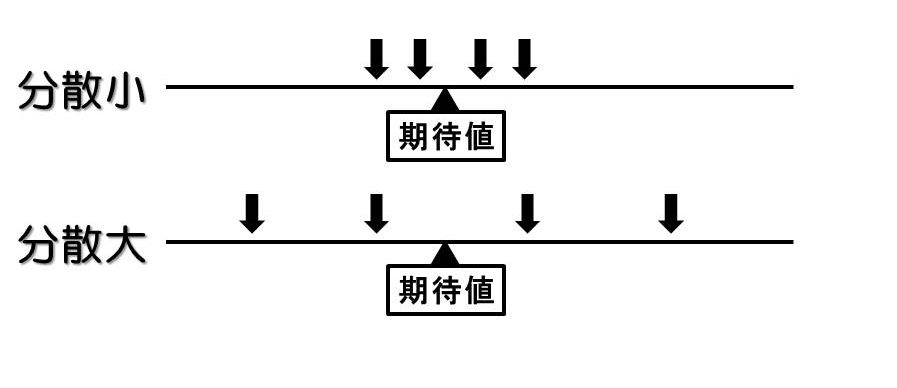
分散の大小を図で表しました。下向きの矢印がリンゴの大きさ(データ)を表しています。

分散は「データが期待値からどれほど離れているか」を表す指標です。
分散が小さければ、データは期待値の周りに集まっています。
分散が大きければ、データは期待値から遠く離れた場所に散らばっています。

データを代表する値として期待値を使おうとしていたはずです。なのに、期待値とデータが離れていたら、「データを代表する値」として期待値を使うことができなくなります。よって、分散が大きければ、期待値は比較の役に立ちません。

期待値を使うとデータの比較が圧倒的に楽になります。しかし、期待値だけしか見ないと、大きな過ちを犯すかもしれません。

8．分散の数理

分散は以下の式で計算されます。

$$\frac{1}{n}\sum_{i=1}^{n}(x_i-μ)^2$$

nがサンプルサイズ、x_iはそのデータの値、µはデータの期待値です。
nで割っていることに注目してください。分散は(x_i-μ)²で計算されるものの平均値なのです。
平均値だということは、少し考え方を拡張すれば、期待値にもできます。
分散の期待値バージョンはこちら。

$$\sum_{i=1}^{n}p_i(x_i-μ)^2$$

1/nがp_iに変わりました。
この式は言い換えるとこうなります。

分散＝(１つ１つのデータ-期待値)²　の期待値

あるいは

分散＝『データと期待値との距離』　の期待値

この式を理解するためには、まず(１つ１つのデータ-期待値)²という部分を理解しなければいけません。なお、（データ－期待値）のことを偏差と呼び、偏差を2乗したものの合計値を偏差平方和と呼びます。
この偏差平方和が大きければ、1つ1つのデータは、期待値から遠く離れています。

例を挙げます。
期待値：0
データその①　：　－0.1
データその②　：　＋0.1
この時の(１つ１つのデータ-期待値)²の合計値は以下の通りです。

$$(-0.1-0)^2+(0.1-0)^2=0.02$$

小さいです。1つ1つのデータが期待値であるところの0からあまり離れていないからです。

一方、以下のようなデータならどうでしょうか。
期待値：0
データその①　：　－100
データその②　：　＋100

$$(-100-0)^2+(100-0)^2=20000$$

大きいです。
期待値からデータが離れていれば、偏差平方和が大きくなることを確認してください。

ゆえに、分散は

分散＝『データと期待値との距離』　の期待値

と解釈されます。

データを代表する値として期待値を使おうとしていたはずです。なのに、期待値とデータが離れていたら、「データを代表する値」として期待値を使うことができなくなります。よって、分散が大きければ、期待値は比較の役に立ちません。

 

9．不偏分散

続いて不偏分散の説明に移ります。

まずは、「不偏」という言葉から説明します。
不偏とは、読んで字のごとく「偏りがない事」を意味します。
偏りのない分散のことが不偏分散です。

それでは、偏りのある分散とは何でしょうか。
それは、普通の分散のことです。前の節の計算式で求めた分散は、偏りのある分散だったのです。

なぜ偏りが生まれてしまうのか、説明します。
ここで気を付けるべきは、サンプリングはあくまでも「一部だけを抽出した結果だ」という事実です。

極端な例で説明します。
この世界にたった一軒しかない貴重な農家があります。この農家にリンゴが100個なっていたとしましょう。
覚えておいてくださいね、100個です。101個目のリンゴなど、この世界に存在しません。この世界に存在するすべてのリンゴの個数は100個です。
そして（少し極端ですが）、リンゴの大きさは1cm、2cmからはじまり、100cmまで、1cm刻みで100種類あったとします。
この時の、リンゴの「本当の」期待値は以下のようになります。

$$\sum_{i=1}^{100}0.01\times{x_i}=50.5$$

ただし

$$x_i=｛1,2,3,…,99,100｝$$

です。

ここで、サンプリングをしました。リンゴは10個しかとりませんでした。無作為に抽出したつもりだったのですが、たまたま小さなリンゴが選ばれてしまったようです。サンプリングの結果は以下のようになりました。

$$x_i=｛1,2,3,4,5,6,7,8,9,10｝$$

偶然、最も小さい1～10cmのリンゴが選ばれたとします。期待値は5.5です。

この時の分散はどうやって計算しますか。
分散の定義を思い出してください。
分散とは「データが期待値からどれだけ離れていると期待できるか」を表した数値でした。

ここで、とても重大な問題が発生します。
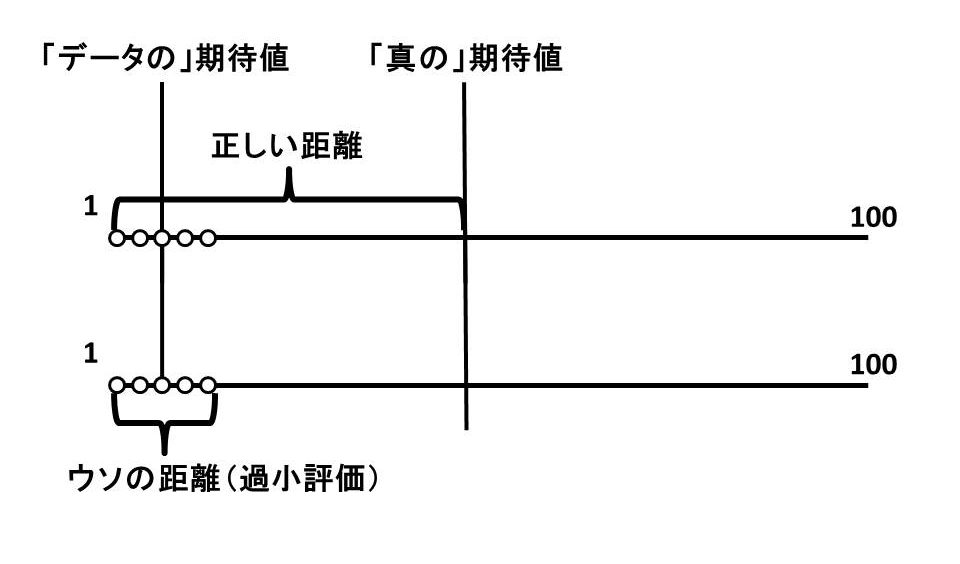
期待値は、「この世界に存在するすべてのリンゴをまとめた時の期待値」をつかうのが正確です。
でも、普通そんな期待値を計算することはできません。今回の例のように、農家の中のリンゴ全て、ならいざ知らず、世界中のリンゴの大きさを全て測って期待値を計算するなんて、不可能です。
よって、「サンプリングした結果計算された期待値」を用いて分散を計算するしかありません。

本当は「50.5から、データ(1~10)がどれだけ離れているか」を計算しなければいけないのに、「5.5から、データ(1~10)がどれだけ離れているか」を計算しているわけです。
当然、データと期待値の距離は小さくなります。分散は過小評価されます。

今回の例では、小さすぎるリンゴを偶然とってきましたが、逆に、91～100cmの大きいリンゴを10個取ってきても、同様に分散は過小評価されます。
ふつうにサンプリングして計算された分散は「小さく偏っている」のです。
なので、その偏りをなくすためには、分散を大きくしなければなりません。

よって、不偏分散は以下のようになります。

$$\frac{1}{n-1}\sum_{i=1}^{n}(x_i-μ)^2$$

ふつうの分散と違って、(n-1)で割っているところに注目してください。分母が小さくなったので、全体の値は大きくなります。「分散」というと、普通はこの不偏分散のことを指します。不偏でない過小評価された分散のことは「標本分散」などと区別して呼ばれます。
偏りをなくすために分散を大きくしているのだということ、ぜひご理解ください。

 

10．標準偏差

標準偏差は不偏分散の平方根（ルート）を取ったものです。

$$\sqrt[]{
\frac{1}{n-1}\sum_{i=1}^{n}(x_i-μ)^2
}$$

なぜ平方根を取るのかというと、そのほうが理解しやすいからです。式を見ればわかるように、分散はデータを2乗しています。ゆえに、単位も2乗されています。
単位が温度の2乗、「℃²」のままでは大変扱いにくいです。
理解を容易にするためにも、ぜひ平方根を取って、標準偏差を使いましょう。

 

11．標準誤差

次は標準誤差です。
標準誤差とは、端的に言うと、サンプルサイズを加味した標準偏差のことです。

式はこちら。なお、σとは標準偏差のことです。よく出てくるので覚えておくと便利です。

$$\sqrt[]{
\frac{\frac{1}{n-1}\sum_{i=1}^{n}(x_i-μ)^2}{n}
}=\frac{σ}{\sqrt[]{n}}$$

標準偏差をサンプルサイズ（の平方根）で割っています。

 

12．期待値の標準偏差としての標準誤差

標準誤差は、標本平均の標準偏差として解釈されます。

標本平均の標準偏差とはちょっとややこしい考え方なので、補足します。

10人の身長を測るという行為を1回したとします。標本平均が計算できます。
10人の身長を測るという行為を、毎回別の人たちに対して100回したとします。
すると、標本平均が100個計算できることになります。

標本平均の期待値とは、そうやって計算された100個の標本平均に対して期待値をとったものです。
標本平均の分散は、100個ある期待値の分散を計算したものです。

ここで重要な性質があります。
標本平均の期待値は、データの期待値と変わらないはずです。
しかし、標本平均の分散は、もともとの分散よりも必ず小さくなります。

10人の身長を測定すると、背の高い人がいることもあるでしょう、背の低い人もいるでしょう。データ（身長）が期待値から離れていることが予想されます。
しかし、身長の期待値（平均値）をとると、そういった「ぶれ」がならされます。背の高い人と低い人の身長を足して2で割ったのが平均ですから、平均値そのものは変化しにくいことが想像つくのではないかと思います。
よって、標本平均を100個とった時の分散は、もともとの身長データの分散よりも小さくなります。

それでは「標本平均の分散」はいくらになるのかというと、標準誤差の2乗になります。
サンプルサイズnは、この場合「10人に調査をした」のでサンプルサイズ10となることに注意してください。

$$\frac{分散}{サンプルサイズ}=\frac{σ^2}{n}$$

すなわち標準誤差とは「標本平均の標準偏差」になるということでした。

次の記事→確率分布と確率変数の基礎

 

参考文献

平均・分散から始める一般化線形モデル入門   この記事を書いた管理人の執筆した本です。 この記事は「平均・分散から始める一般化線形モデル入門」から入門編だけを抜粋して大幅に加筆、修正したものになります。 特に第1部のt検定(数式なし)とt検定(数式あり)の内容を多く反映しています。この2つの章は、全文をサイトに公開しているのでよろしければリンクからご覧になってください。 統計学の基礎の基礎から始めて、一般化線形モデルというやや高度な手法が使えるところまで説明している本です。このサイトで統計学の基礎を学ばれた後に読まれると、ちょうどよいかと思います。

「平均・分散から始める一般化線形モデル入門」を購入されるときの注意
定価は2500円(消費税8%で2700円)ですが、Amazonさんなどでは在庫が不足しており、中古価格が高騰することがあります。
重版したので出版社には在庫が残っています。出版社のサイトからですと送料無料・書籍代は後払い・最短翌日出荷で、確実に定価で手に入ります。
以下のネット書店も併せてご利用ください。

 

マンガでわかる統計学   この記事を書くのに参考にした本です。 漫画とはいえ内容はしっかりしており、統計学の基礎を学ぶのに最適です。

統計学入門 (基礎統計学)   この記事を書くのに参考にした本です。 かなり内容の濃い、言い方を変えると難しい本ですが、是非一度読まれることをお勧めします。 20年間売れ続けている、統計学のロングセラーです。

スポンサードリンク

 
2016年5月14日：新規作成
2017年4月16日：リンクの追加・修正など
2017年5月26日：目次から本文中へ移動できるようにリンクを追加
2019年3月19日：本文を一部修正（標準誤差の説明）