ニューラルネットワークの考え方
最終更新:2017年7月12日
ニューラルネットワークの考え方ついて説明します。
応用例としては時系列データを扱いますが、基本的な考え方は変わりませんので、ニューラルネットワークの仕組みを学びたいというだけの方でも読む意味はあるかと思います。
この記事ではニューラルネットワークの基本について説明したのちに、nnetやforecastパッケージを用いた、時系列データへのニューラルネットワークの適用を試みます。
なお、特に断りがない限り、定量データを予測する「回帰」問題のみを扱うことに注意してください。
コードはこちらに置いてあります。
スポンサードリンク
目次
- ニューラルネットワークの考え方
- nnetの使い方
- 飛行機乗客数のモデル化
- ヤマネコ個体数データのモデル化
- 発展的な話題
- リミットサイクル
- 予測区間の計算と図示
1.ニューラルネットワークの考え方
モデルの概要
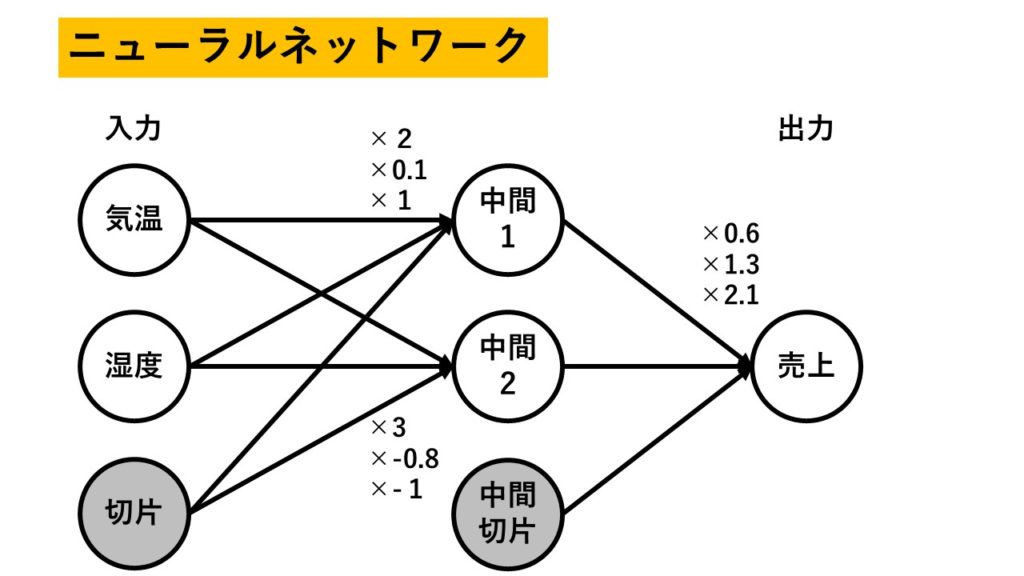
ニューラルネットワークは重回帰分析と比較するとその特徴が分かりよいです。
例えば、気温と湿度からビールの売り上げを予測するとしましょう。
古典的な重回帰分析の構成図とニューラルネットワークの構成図を比較してみましょう。
実質、この違いがニューラルネットワークの特徴のすべてだといえます。
こちらが重回帰分析。
ビールの売り上げを『気温×4 + 湿度×0.5 + 2(切片)』でモデル化していると考えてください。
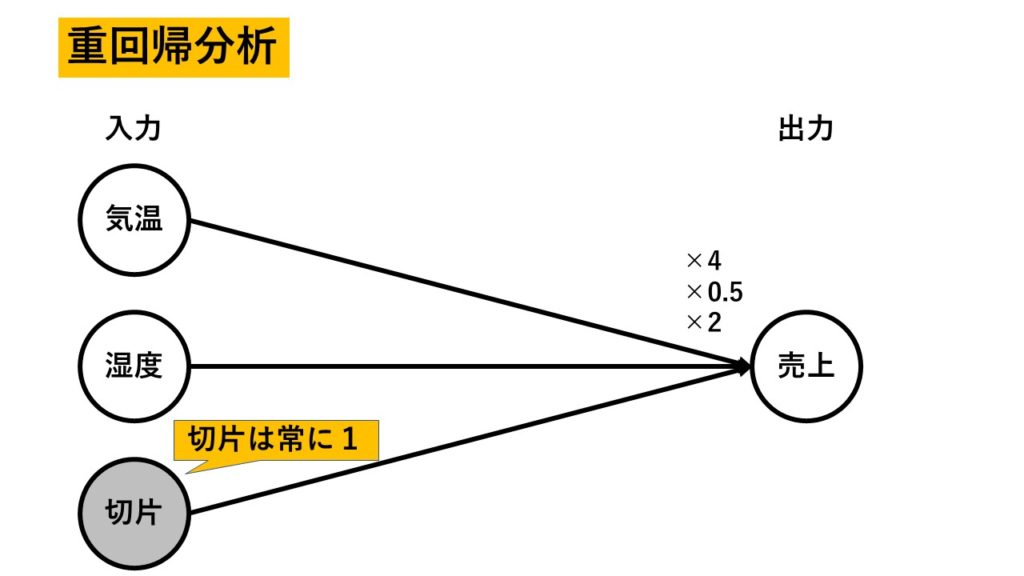
『×4』などと書かれている部分が、傾きなどの「パラメタ」となります。
なお、ニューラルネットワークの場合は「傾き」ではなく「重み」といわれることが普通です。
重回帰分析における「切片」の取り扱いに注意してください。
切片は「常に1である説明変数」だとみなします。で、「常に1である説明変数」にかかる係数(傾き・重み)がいくらかという風に表現します(図の場合は2ですね)。
この書き方にすると、ニューラルネットワークと同じになります。
ニューラルネットワークの場合はこの切片を「バイアス」と呼びます(図では重回帰分析に合わせてますが)。
なお、ニューラルネットワークにおいて、図の左側を「入力層」真ん中を「中間層」右側を「出力層」と呼びます。
この図のパラメタを使うと、各々、以下の計算式を使って売り上げを予測することになります。
重回帰分析
売上 = 気温×4 + 湿度×0.5 + 2
ニューラルネットワーク
中間1 = 気温×2 + 湿度× 0.1 + 1
中間2 = 気温×3 + 湿度×(-0.8) – 1
売上 = 「中間1」×0.6 + 「中間2」×1.3 + 2.1
中間層が入ってきているため、モデルを複雑にできるようになったんですね。
今回は中間層に2つしか置きませんでしたが、これを3つとか4つ、あるいは50個などに増やしていくと、いくらでも複雑なモデルを作ることができます。
なお、勘違いされないように補足をしておきますと、ここでの「中間層をサイズを増やす」とは以下の図のように縦に伸ばす行為になります。
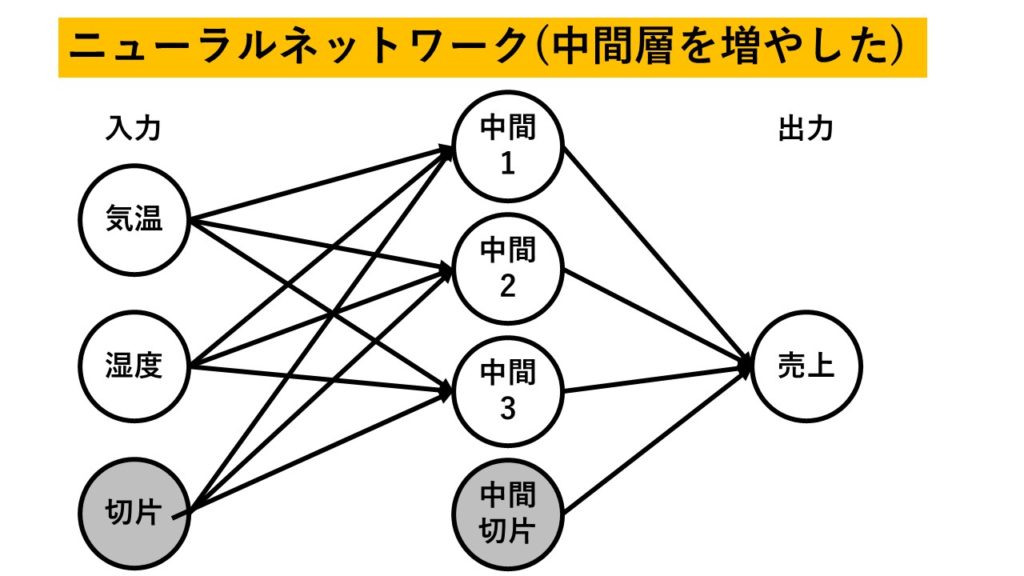
最近はやりの深層学習(ディープラーニング)はこんな感じ↓で横に伸びます。
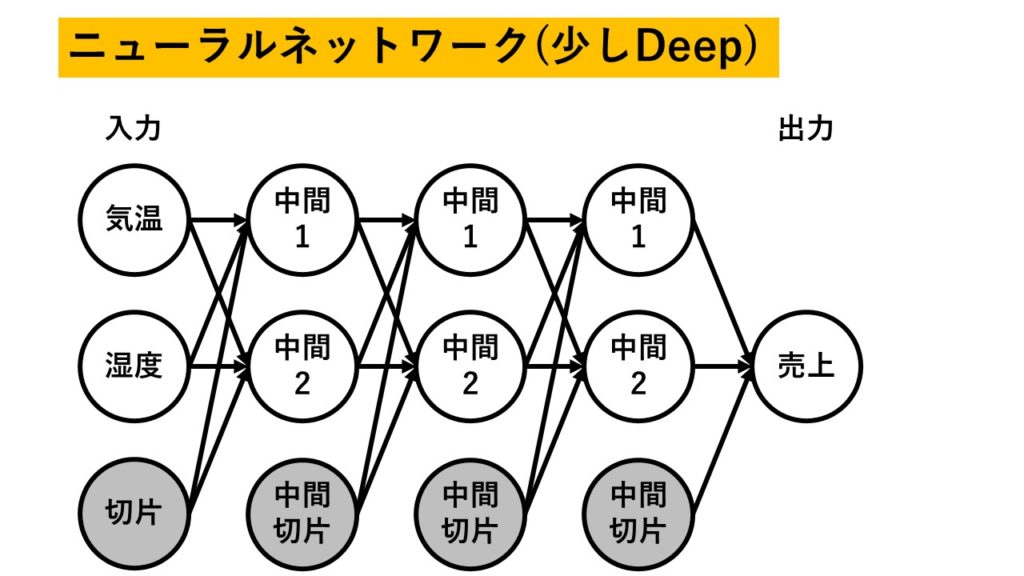
これからライブラリを使ってニューラルネットワークを推定することになります。その時、中間層のサイズを設定することができます。
できるんですが、これを増やしたところで深層学習にはならないんだよということだけご理解ください。
なお、モデルのパラメタは「予測誤差が最小になる」ように、繰り返し計算を行ってチューニングされます。
nnetでは準ニュートン法「BFGS」が使われているようです。
以下、発展的な話題をいくつか載せますが、これが分からなくても支障ありませんので、難しければ飛ばしてください。
発展的な話題1:分類問題との違い
分類問題の場合は、中間層→出力層に行く際に、少し変換がかけられます。
具体的には「ロジスティック関数」などが適用されます。
例えば、画像があって、それがリンゴなのかミカンなのかを判別したいとしましょう。
このとき「リンゴである確率」が予測値として出てくると便利ですよね。
このとき、ロジスティック関数を間に挟むと「出力が0~1の間に収まる」ようになります。
これが便利なので、分類問題の場合には、間にちょっとした変換を挟んでいるんだよということだけ覚えておいてください。
発展的な話題2:パラメタ推定における深層学習との違い
先に少し図で示したように、ニューラルネットワークを右にどんどん伸ばしていけば深層学習になります。しかし、横に伸びると、どうしてもモデルが複雑になるため、普通のニューラルネットワークにおけるパラメタ推定の手法が使えなくなります。
重回帰分析ですと方程式を一発解くだけでパラメタが求まるのですが、ニューラルネットワークの場合はそうもいきません。
数値的に、繰り返し計算を行ってパラメタを求めます。
先に申し上げたように、nnetパッケージでは準ニュートン法「BFGS」を使っているようです。
(マニュアルを見ると、Rのoptim関数をそのまま使っている様子です)
ですが、ニュートン法のような「高機能な」最適化アルゴリズムには「計算が複雑である」という欠点があります。
準ニュートン法も同じです。
この問題は、モデルが複雑になる深層学習ではさらに顕著となります。もう、準ニュートン法などの高尚な手法は使えません。
そこで、代わりに「勾配降下法」という最適化手法を使います。
これははっきりというと準ニュートン法と比べて明らかに効率の悪い最適化アルゴリズムなのですが、計算が簡単なので、深層学習ではもはや「これを使うしかない」という状況となっています。
また、モデルが複雑になると、勾配降下法を使ってもなかなかちゃんとパラメタが推定できないらしく、相当の工夫がなされています。
そのため、深層学習の本を読むとパラメタ推定に多くの紙数が割かれています。
今回のような「普通の」ニューラルネットワークの場合だから、これほど簡単な説明で済んだのだよということだけ覚えておいてください。
発展的な話題3:微分と誤差逆伝播法(バックプロパゲーション)
パラメタを推定するためには、関数を微分する必要があります。
微分とは、高校生の時に習いましたが、傾きを求める方法でした。
接線の傾きをひたすら計算させられた記憶があるのではないでしょうか。
パラメタ推定の際には「パラメタを変えた時の予測誤差の変化」を調べます。
例えば、パラメタを0.1大きくしたら、誤差が減ったな、とか、逆に0.1小さくしたら誤差が大きくなっちゃったとか。
これであれば「パラメタを大きくすればいいんだ」ということが分かりますね。そしたら誤差が減る。
微分を使って傾き、すなわち変化の度合いがプラスなのかマイナスなのかを調べることによって、最適な(最も予測誤差が小さくなる)パラメタを推定することができるのです。
で、この微分の計算が、ニューラルネットワークの場合は難しいです。
そこで「誤差逆伝播法(バックプロパゲーション)」という方法が使われます。
誤差逆伝播法とは、あくまでも「効率的に微分の計算をするアルゴリズム」なのだということだけ覚えておいてください。
誤差逆伝播はパラメタ推定の原理を学びたいときにはとても重要な考えとなります。
逆に言えば、R言語を使ってモデルを構築する・作られたモデルを解釈する、ときにはあまり気にしなくて大丈夫です。
2.nnetの使い方
ニューラルネットワークは、nnetというパッケージを使うことで計算ができます。
『library(nnet)』と実行すれば準備完了です。
コードはこちらに置いてあります。
今回は、自動車の速度と、停止距離の関係のデータを使うことにします。
> # 自動車の速度と、停止距離の関係 > cars speed dist 1 4 2 2 4 10 3 7 4 4 7 22 5 8 16 ・・・中略・・・ 46 24 70 47 24 92 48 24 93 49 24 120 50 25 85
まずは比較のため、普通の線形回帰を推定してみます。
# 普通の線形回帰 lm_model <- lm(dist ~ speed, data=cars)
次はニューラルネットワークです。nnetという関数を使います。
# ニューラルネットワーク nnet_model <- nnet( dist ~ speed, data=cars, size=40, linout=TRUE, maxit=1000 )
基本的には普通の線形回帰と同じように、formulaとデータを指定します。
予測したい対象が「~」の左側、説明変数が右側に来ます。今回は、速度という説明変数を使って、停止にかかった距離を予測します。
以下、その他の引数の補足をします。
- size=40 が中間層のサイズの指定です。線形回帰との違いを見てほしかったので、あえて複雑なモデルにしました。普通は2~3で十分です。
- linout=TRUE は、回帰をしますよという指定です。ここはデフォルトではFALSEになっており、そのままだと分類をしてしまうので注意が必要です。
- maxit=1000 は、パラメタ推定のために、最大何回まで反復計算をするのを許すか、という回数の指定です。多い方が正確にパラメタを推定できます。
続いて、ニューラルネットワークの特徴を見ていただくために、あえて中間層をなくしたものを作ってみます。
これは線形回帰と同じ結果となるはずです。
『size=0,skip=TRUE』と指定してあることに注意してください。
# 中間層をなくしたニューラルネットワーク(実質線形回帰と同じ) lm_modoki <- nnet( dist ~ speed, data=cars, size=0,skip=TRUE, linout=TRUE )
ニューラルネットワークの重みと、回帰分析の係数を比較してみます。
> # 係数が同じになっている
> summary(lm_modoki)
a 1-0-1 network with 2 weights
options were - skip-layer connections linear output units
b->o i1->o
-17.58 3.93
> lm_model
Call:
lm(formula = dist ~ speed, data = cars)
Coefficients:
(Intercept) speed
-17.579 3.932
ニューラルネットの結果における『b->o』がバイアスの重み、『i1->o 』が説明変数(speed)の重みです。
回帰分析の係数とまったく同じ値になっていることに注目してください。
中間層の無いニューラルネットワークは、回帰分析と何ら変わりはないのです。
モデルの当てはめ結果(予測値)は『fit』または『fitted.values』という要素に入っているため、それを図示してみます。
# 図示
plot(dist ~ speed, cars)
lines(lm_model$fit ~ cars$speed)
lines(nnet_model$fitted.values ~ cars$speed, col=2)
lines(lm_modoki$fitted.values ~ cars$speed, col=4, lty=2, lwd=2)
legend(
"topleft",
legend=c("線形回帰", "ニューラルネット", "中間層がないニューラルネット"),
col=c(1,2,4),
lty=c(1,1,2)
)
結果はこちら。
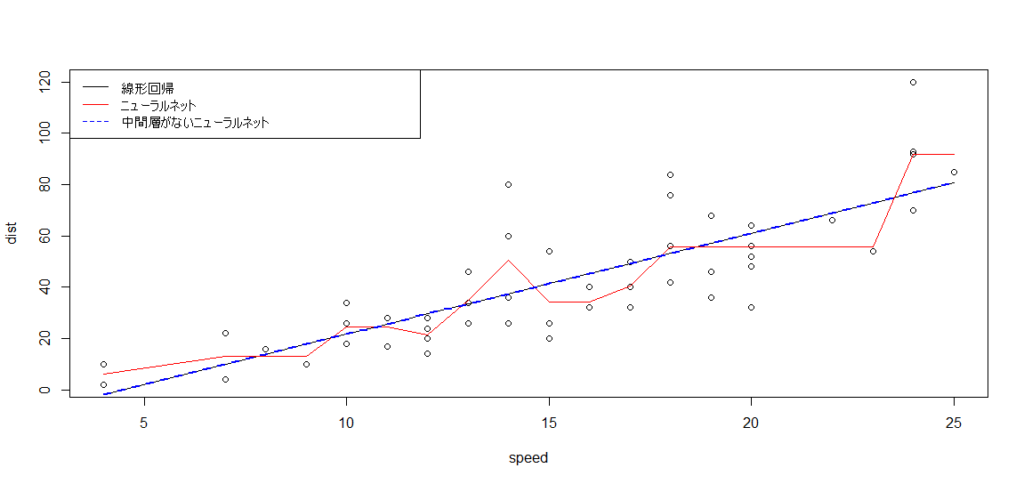
青の点線であらわした「中間層無しのニューラルネット」と、線形回帰の結果が同じになっていることを確認してください。
また、赤の線であらわしたニューラルネットワークの予測値がグネグネと曲がっていることにも注目してください。
このように、非線形な関係があったとしてもニューラルネットワークならば予測をすることが可能です。これが中間層があることの威力といえるでしょう。
なお、ここでは基本的な使い方だけを説明しました。
中間層のサイズなど「あらかじめ指定しなければならないパラメタ」のことをハイパーパラメタと呼ぶのですが、こいつのチューニングなど、もっと凝ったことをしてみたいという方は『Rによる機械学習:caretパッケージの使い方』を参照してください。
スポンサードリンク
3.飛行機乗客数のモデル化
次は時系列データに対してニューラルネットワークを適用してみます。
気温と湿度から売上を予測したのと同じように、過去のデータから未来を予測します。これが時系列分析です。
入力としては、1期前(日単位データならば一日間、月単位データならばひと月前)のデータと、1周期前(月単位データならば前年など)を使います。
この2つがあれば、「昨日の売上が高ければ今日もよく売れるだろう」とか「毎年8月には売り上げが伸びるんだ」とかいう状況をモデル化することができます。
やってみます。
forecastというパッケージをインストールしてから『library(forecast)』としたら準備完了です。
今回は飛行機乗客数のデータを使います。
> # 飛行機乗客数のデータ
> AirPassengers
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949 112 118 132 129 121 135 148 148 136 119 104 118
1950 115 126 141 135 125 149 170 170 158 133 114 140
1951 145 150 178 163 172 178 199 199 184 162 146 166
1952 171 180 193 181 183 218 230 242 209 191 172 194
1953 196 196 236 235 229 243 264 272 237 211 180 201
1954 204 188 235 227 234 264 302 293 259 229 203 229
1955 242 233 267 269 270 315 364 347 312 274 237 278
1956 284 277 317 313 318 374 413 405 355 306 271 306
1957 315 301 356 348 355 422 465 467 404 347 305 336
1958 340 318 362 348 363 435 491 505 404 359 310 337
1959 360 342 406 396 420 472 548 559 463 407 362 405
1960 417 391 419 461 472 535 622 606 508 461 390 432
このデータの良いところは、年単位での周期性があるということ、また右肩上がりのトレンドがあるところです。
この2つをうまくモデル化しなければ、予測はできません。
『予測の評価方法』でも示したように、モデルを作る時に使うデータ(訓練データ)と評価のためのテストデータは分けた方が良いです。
このデータも2つに分けましょう。
# 訓練データとテストデータに分ける train_air <- window(AirPassengers, end = c(1957, 12)) test_air <- window(AirPassengers, start = c(1958, 1))
いよいよニューラルネットワークによるモデル化です。
nnetを使ってもよいのですが、もっと便利な関数が用意されているのでそれを使います。
実質1行で終わります。『nnetar』という関数を使います。
# 時系列データへのニューラルネットワーク set.seed(0) nn_air <- nnetar(train_air, maxit=1000)
『nnetar』関数に、訓練データと、パラメタ推定の際の繰り返し数(maxit)を指定するだけです。
実は『maxit』は指定しなくても動きます。
『nnetar』関数は以下の特徴を持っています。
- nnet関数を内部で使用している
- nnet関数で使われる設定は、『nnetar』関数でも設定することができます
- ただし、『linout=TRUE』の指定はいらないようです。常にFALSEになっているようです
- 何期前までのデータを使うかは、自動で選んでくれる
- 自己回帰モデルというモデルを別途推定して、その時のAIC最小となる次数を採用します
- 自己回帰モデルについては時系列解析理論編を参照してください
- 『p』という引数で指定してやることもできます(pは小文字)。『p=2』とすると、2期前まで(1期前と2期前)のデータを使用します
- 周期性がある場合は、自動で1周期前のデータを説明変数に入れてくれる
- 元データがts形式のデータである場合のみやってくれます
- frequencyを見て、周期を判断しています(frequency(AirPassengers)と実行すれば、周期がどのように元データに対して設定されていたかが分かります)
- 『P』という引数で指定してやることもできます(Pは大文字)。『P=2』ならば、2周期前まで使うことになります
- 中間層のサイズも自動で設定してくれます
- 割と適当に設定されているようです
- 『size』という引数で指定してやることもできます。
- パラメタの初期値依存をなくすために、複数の初期値で推定されたモデルを保持しています
- ややこしいので後述します
推定結果は以下のようになります。
> # 推定された結果 > nn_air Series: train_air Model: NNAR(1,1,2)[12] Call: nnetar(y = train_air, maxit = 1000) Average of 20 networks, each of which is a 2-2-1 network with 9 weights options were - linear output units sigma^2 estimated as 129.7
4行目の『NNAR(1,1,2)[12] 』に注目してください。
これは以下のような意味となります。
NNAR(p, P, size)[freqency]
すなわち
NNAR(何期前までのデータを使うか,過去の周期をどれだけ使うか,中間層のサイズ)[周期]
もうちょっと推定結果を調べてみましょう。
> # 中身を確認
> names(nn_air)
[1] "x" "m" "p" "P" "scalex" "size" "subset" "model" "nnetargs" "fitted" "residuals"
[12] "lags" "series" "method" "call"
> summary(nn_air$model)
Length Class Mode
[1,] 15 nnet list
[2,] 15 nnet list
[3,] 15 nnet list
[4,] 15 nnet list
[5,] 15 nnet list
・・・中略・・・
[16,] 15 nnet list
[17,] 15 nnet list
[18,] 15 nnet list
[19,] 15 nnet list
[20,] 15 nnet list
namesという関数を使うと、内部でどんな情報を持っているのかがわかります。modelというものが見つかったので中身を見ていると、20個のnnetの推定結果が出てきました。
nnetの結果が20個も格納されているのは、パラメタ推定の頑健性を高めるためだと思います。
パラメタの初期値は、根拠なくテキトーに決めてやるしかありません。
それが怖いので、nnetar関数では、毎回パラメタの初期値を変えて何度も何度もパラメタ推定を行うのです。
なお、デフォルトでは20個の初期値を使って20回nnetによるモデル化が行われます。
このモデルを20個保存しておいて、予測する際は、20個のモデルの平均値を予測値として使うようです。
何個のモデルを作るかは『repeats』という引数で指定できます。
下の例では2個にしてみました。
> # repeatsを変更すると、モデルの数も変わる(デフォルトは20)
> summary(nnetar(train_air, maxit=1000, repeats=2)$model)
Length Class Mode
[1,] 15 nnet list
[2,] 15 nnet list
なお、推定された重みがいくらになったのか調べることもできます。
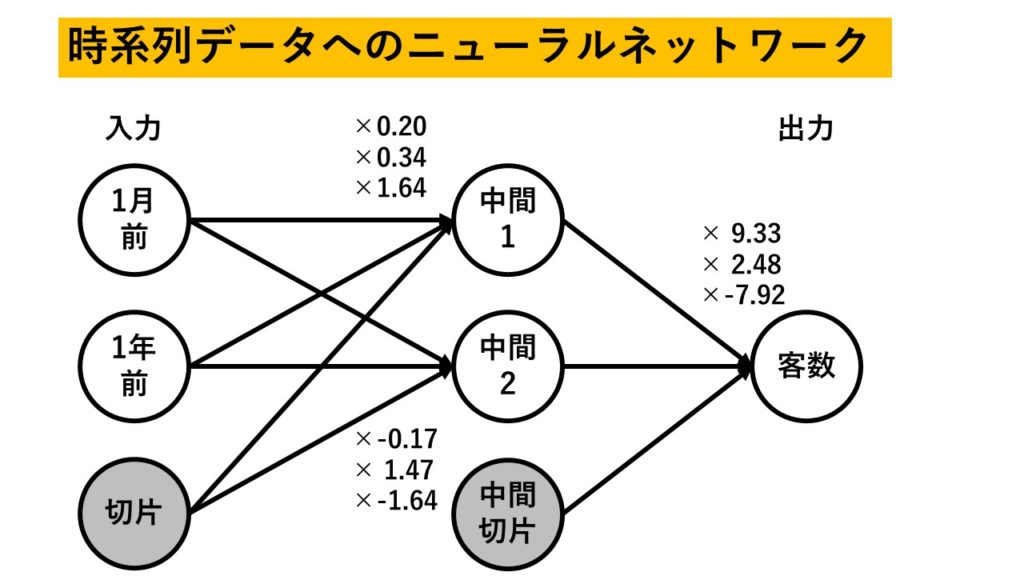
> # 推定された重みを確認する > summary(nn_air$model[[1]]) a 2-2-1 network with 9 weights options were - linear output units b->h1 i1->h1 i2->h1 1.64 0.20 0.34 b->h2 i1->h2 i2->h2 -1.64 -0.17 1.47 b->o h1->o h2->o -7.92 9.33 2.48
今回は、比較のためにSARIMAモデルも推定してみます。
SARIMAについては『時系列解析理論編』を参照してください
# 比較のためにSARIMAモデルも使う sarima_air <- auto.arima(train_air, ic = "aic")
結果はこちら。
> sarima_air
Series: train_air
ARIMA(0,1,1)(0,1,0)[12]
Coefficients:
ma1
-0.2389
s.e. 0.1053
sigma^2 estimated as 94.11: log likelihood=-350.19
AIC=704.38 AICc=704.51 BIC=709.48
参考までに、SARIMAとNNARのパラメタには以下の関係があります。
NNAR(p, P, size)[freqency]
ARIMA(p,0,0)(P,0,0)[freqency]
SARIMAでも、「前期の値」と「前の周期の値」が使われているんだということだけここではご理解ください。
なので、ここでの予測精度の比較は、純粋にモデルの違いがもたらす違いということになります。
3年後までを予測します。
forecastという関数を使います。
# 3年後までを予測する # nnet f_nn_air <- forecast(nn_air, h = 36)$mean # sarima f_sarima_air <- forecast(sarima_air, h=36)$mean
『h=36』と指定することで、36か月先、すなわち3年後までを予測することになります。
予測値のみを保存しておきました。
予測誤差の大小を比較します。
> # 予測精度の比較
> accuracy(f_nn_air, test_air)
ME RMSE MAE MPE MAPE ACF1 Theil's U
Test set -33.69774 46.45494 42.91255 -8.930072 10.46267 0.57663 1.010223
> accuracy(f_sarima_air, test_air)
ME RMSE MAE MPE MAPE ACF1 Theil’s U
Test set -2.912497 21.91507 17.80556 -1.410825 4.187092 0.6041376 0.4539029
1つ目がニューラルネットワーク、2つ目がSARIMAです。
accuracy関数の詳細は『予測の評価方法』を参照してください。
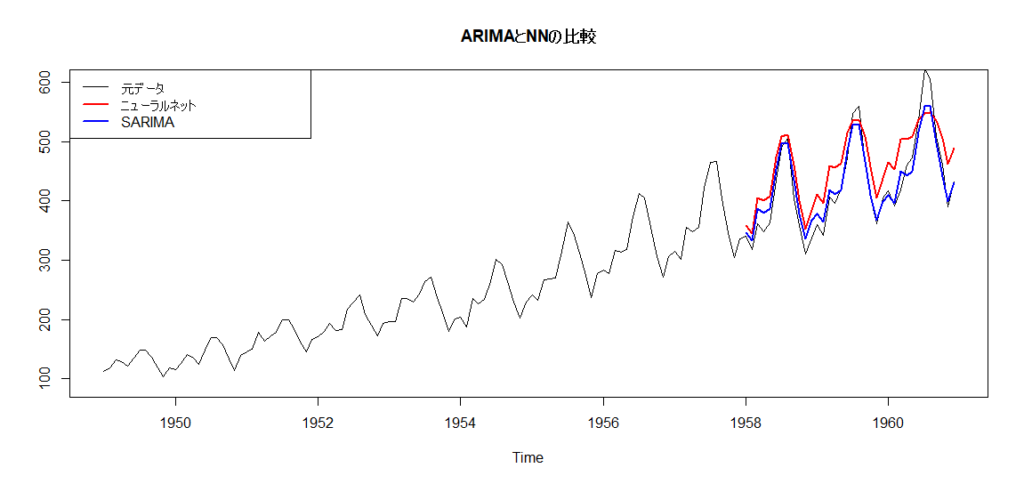
とはいえ、これを見ると、小さければ小さいほうが良いとされる『RMSE』は断然SARIMAのほうが低くなっています。
グラフを見てもそれがわかります。
# 予測結果のグラフ
ts.plot(
AirPassengers,
f_nn_air,
f_sarima_air,
ylim=c(90, 600),
col=c(1,2,4),
lwd = c(1,2,2),
main="ARIMAとNNの比較"
)
legend(
"topleft",
legend=c("元データ", "ニューラルネット","SARIMA"),
col=c(1,2,4),
lwd=c(1,2,2)
)
やはり、SARIMAのほうがうまくいっているようです。
このように、変化が線形であったり、周期も明確である場合は、普通の線形時系列モデルのほうが精度が良くなることもあります。
機械学習法を使うと、常に予測精度が上がる、というわけではないということだけご理解ください。
4.ヤマネコ個体数データのモデル化
次は、ヤマネコ個体数データを対象としてみます。
これは非線形に変わっていくことが予想されるため、ニューラルネットワークのほうが適しています。
Rにもともと入っている、lynxというデータを使います。
> # ----------------------------------------------------------- > # ヤマネコ個体数データのモデル化 > # ----------------------------------------------------------- > lynx Time Series: Start = 1821 End = 1934 Frequency = 1 [1] 269 321 585 871 1475 2821 3928 5943 4950 2577 523 98 184 279 409 2285 2685 3409 1824 409 151 45 68 213 546 1033 [27] 2129 2536 957 361 377 225 360 731 1638 2725 2871 2119 684 299 236 245 552 1623 3311 6721 4254 687 255 473 358 784 [53] 1594 1676 2251 1426 756 299 201 229 469 736 2042 2811 4431 2511 389 73 39 49 59 188 377 1292 4031 3495 587 105 [79] 153 387 758 1307 3465 6991 6313 3794 1836 345 382 808 1388 2713 3800 3091 2985 3790 674 81 80 108 229 399 1132 2432 [105] 3574 2935 1537 529 485 662 1000 1590 2657 3396
これは『Frequency = 1』となっていることから、年1回のデータであることがわかります。
『Frequency = 1』の場合は、周期変動をモデルの中に入れることは難しいです。
これもSARIMAが使いにくい理由となります。
例によって訓練データとテストデータに分けます。
ただし、訓練データは、対数変換をしておきました。
対数変換してからモデル化~予測の段階で元に戻す、とした方が予測精度が高くなったためです。
# 訓練データとテストデータに分ける train_lynx <- log(window(lynx, end = c(1920))) test_lynx <- window(lynx, start = c(1921))
まずはニューラルネットワークとARIMAモデルを推定します。
(季節成分がないので、SARIMAではなくARIMAになります)
# 時系列データへのニューラルネットワーク nn_lynx <- nnetar(train_lynx, decay=0.5, maxit=1000) # 比較のためにARIMAモデルも使う sarima_lynx <- auto.arima(train_lynx, ic = "aic")
結果はこちら。
> # 推定結果
> nn_lynx
Series: train_lynx
Model: NNAR(11,6)
Call: nnetar(y = train_lynx, decay = 0.5, maxit = 1000)
Average of 20 networks, each of which is
a 11-6-1 network with 79 weights
options were - linear output units decay=0.5
sigma^2 estimated as 0.2106
> sarima_lynx
Series: train_lynx
ARIMA(3,0,2) with non-zero mean
Coefficients:
ar1 ar2 ar3 ma1 ma2 intercept
0.7797 0.2370 -0.5875 0.5690 -0.3260 6.6506
s.e. 0.1370 0.1699 0.1069 0.1374 0.1079 0.1137
sigma^2 estimated as 0.2834: log likelihood=-77.35
AIC=168.7 AICc=169.92 BIC=186.94
ニューラルネットワークでは『NNAR(11,6) 』となったため、11期前までのデータを使い、中間層のサイズは6個となったことがわかります。
周期成分が入っていないため、2つしか次数が表示されていないことに注意してください。
一方のARIMAは『ARIMA(3,0,2)』となり、3期前までのデータのみを使うことになりました。
使われている次数が少ないのも、なんだか不公平なので、11期前まで使うバージョンも推定しておきました。
> # 次数を合わせるため、11期前までを使ったARIMAも作る
> arima_lynx_11 <- Arima(train_lynx, order=c(11,0,10))
> arima_lynx_11
Series: train_lynx
ARIMA(11,0,10) with non-zero mean
Coefficients:
ar1 ar2 ar3 ar4 ar5 ar6 ar7 ar8 ar9 ar10 ar11 ma1 ma2 ma3 ma4
1.2199 -0.0937 -0.5542 0.3427 0.3591 -0.7062 0.3786 0.0469 -0.1274 0.4855 -0.5293 -0.2319 -0.8251 0.2632 -0.2071
s.e. 0.2516 0.4622 0.4113 0.3494 0.3963 0.3734 0.4641 0.4647 0.2853 0.2929 0.1834 0.2851 0.2913 0.3378 0.3579
ma5 ma6 ma7 ma8 ma9 ma10 intercept
-0.7982 0.3648 0.1920 -0.1797 0.4465 -0.0175 6.5937
s.e. 0.2982 0.3387 0.3927 0.2924 0.2525 0.1986 0.0057
sigma^2 estimated as 0.1767: log likelihood=-53.16
AIC=152.32 AICc=166.85 BIC=212.24
予測します。
# 予測する # nnet f_nn_lynx <- forecast(nn_lynx, h = 14)$mean # arima f_arima_lynx <- forecast(arima_lynx, h=14)$mean f_arima_lynx_11 <- forecast(arima_lynx_11, h=14)$mean
予測精度の比較です。
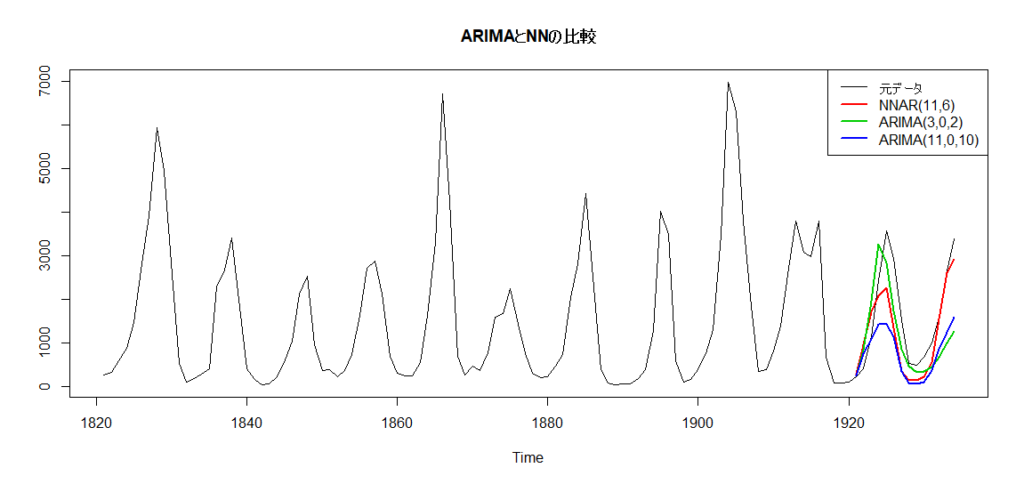
今度はニューラルネットワークが最も良い結果となりました。
> # 予測精度の比較
> accuracy(exp(f_nn_lynx), test_lynx)
ME RMSE MAE MPE MAPE ACF1 Theil's U
Test set 387.0486 722.9746 558.028 17.43471 47.91238 0.6645754 1.19953
> accuracy(exp(f_arima_lynx), test_lynx)
ME RMSE MAE MPE MAPE ACF1 Theil’s U
Test set 450.5771 948.6697 751.7236 15.50991 46.82244 0.6050874 1.298077
> accuracy(exp(f_arima_lynx_11), test_lynx)
ME RMSE MAE MPE MAPE ACF1 Theil’s U
Test set 846.69 1111.814 898.8773 44.39147 57.99759 0.5992318 1.103086
図示してみます。
# 予測結果のグラフ
ts.plot(
lynx,
exp(f_nn_lynx),
exp(f_arima_lynx),
exp(f_arima_lynx_11),
col=c(1,2,3,4),
lwd = c(1,2,2,2),
main="ARIMAとNNの比較"
)
legend(
"topright",
legend=c("元データ", "NNAR(11,6)","ARIMA(3,0,2)","ARIMA(11,0,10)"),
col=c(1,2,3,4),
lwd=c(1,2,2,2)
)
短期で見るとARIMA(3,0,2)のほうがよさそうでしたが、徐々に元データと乖離していき、ニューラルネットワークのほうが精度が高くなっていきました。
ニューラルネットワークは銀の弾丸とはなりえませんが、データによっては高い精度を誇ります。
また、ニューラルネットワークの基本的な考え方はかなりシンプルです。
深層学習などの複雑な手法を学ぶ前に基礎を抑えておくとよろしいかと思います。
発展的な話題
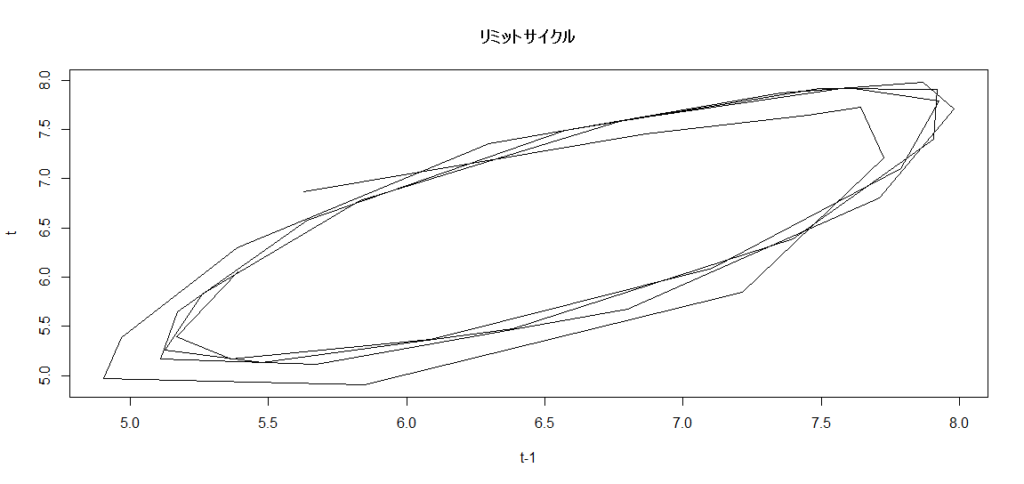
リミットサイクル
少し発展的な話題をいくつか載せます。
まずは、周期変動を確認する方法です。
季節変動をする場合などは、簡単に周期があることを確認できるのですが、ヤマネコ個体数データのように、周期がどのように回ってくるのかわからない場合があります。
この場合、推定されたモデルにおける「リミットサイクル」を図示すると、その特徴がわかることもあります。
(今回の例では、厳密には収束していなさそうですが……)
まずはグラフを描くコードを一気に載せます。
## リミットサイクルを描く # 長期間における周期変動を調べる f_nn_lynx_long <- forecast(nn_lynx, h = 40)$mean forecast_lag <- embed(f_nn_lynx_long, 2) plot( forecast_lag[,1] ~ forecast_lag[,2], type="l", main="リミットサイクル", xlab="t-1", ylab="t" )
まず、3行目において、40期先まで、やや長期の予測を出しました。
この上で、『embed』という関数を使います。
これは例えば以下のように動きます。
> embed(1:5, 2)
[,1] [,2]
[1,] 2 1
[2,] 3 2
[3,] 4 3
[4,] 5 4
1,2,3,4,5という数値があったら、それを1つずらした系列のペアを作ることができます。
時系列データの場合は「1期前と今日」のペアを作ることになります。
『embed』を使って、予測結果における「前期の予測と今期の予測」結果のグラフを描きます。
縦軸か「今期」の予測結果で、横軸が「前期」の予測結果です。
円を描くように動いているので、周期的な変動があることが想像できます。
予測区間の計算と図示
ブートストラップ法を用いた予測区間を計算することもできます。
『bootstrap = T』として、ブートストラップ法を使うという指定をします。
『level = c(80,95)』として、「80%、95%点」を計算するという指定をします。
『PI=T』で、予測区間を表示させます。
結果はこちら。
> ## ニューラルネットワークにおける予測区間
> # ブートストラップ法を使って、予測区間を出す
> f_nn_lynx2 <- forecast(
+ nn_lynx, h = 14,
+ bootstrap = T, level = c(80,95), PI=T
+ )
> f_nn_lynx2
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1921 5.627909 4.931523 6.143173 4.689760 6.636037
1922 6.863555 6.039447 7.620499 5.508386 8.170518
1923 7.451249 6.508720 8.308004 5.967315 8.677959
1924 7.640921 6.685964 8.429381 6.113729 8.865269
1925 7.724769 6.747281 8.512531 6.239102 8.872874
1926 7.212632 6.196637 8.071838 5.605153 8.557101
1927 5.845429 4.872105 6.743532 4.385073 7.312183
1928 4.905819 4.102377 5.743205 3.601943 6.196678
1929 4.967856 4.167599 5.774635 3.813681 6.190640
1930 5.386484 4.623502 6.282375 4.154876 6.757753
1931 6.298354 5.383325 7.422167 4.886026 7.983876
1932 7.351531 6.292109 8.454507 5.605526 8.960327
1933 7.868560 6.761603 8.793417 6.052677 9.216183
1934 7.979574 6.774456 8.807896 6.168602 9.168506
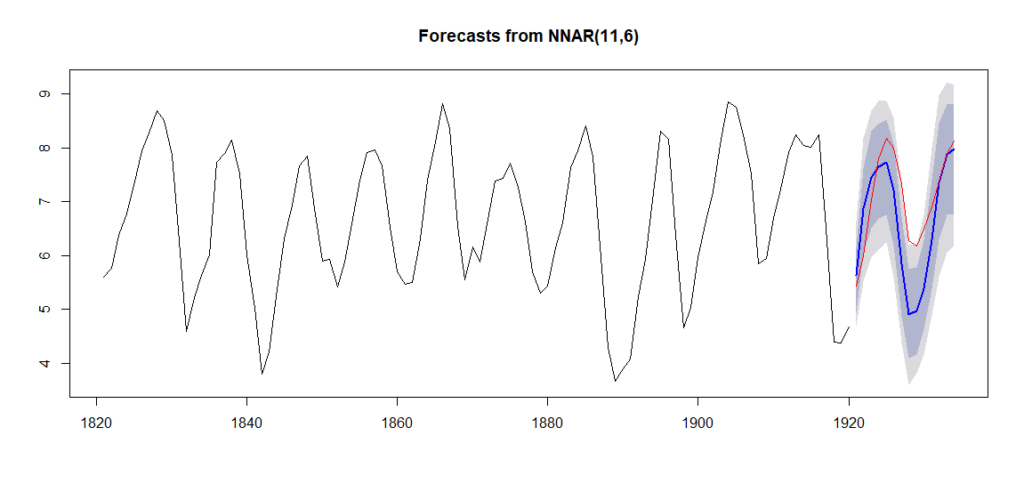
図示もできます。
# 予測区間のあるグラフ plot(f_nn_lynx2) lines(log(test_lynx), col=2)
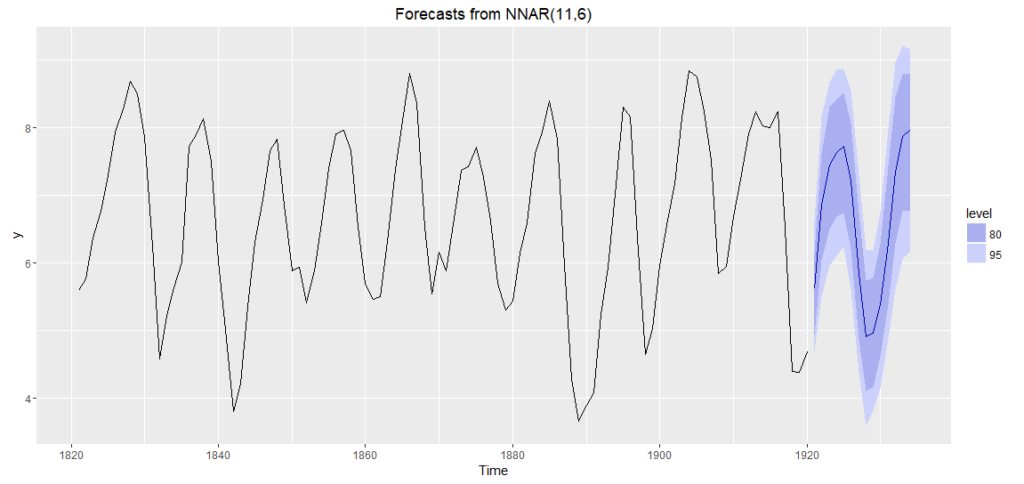
ggplot2を使うと、より美麗なグラフを描くことができます。
# ggplot2を使ったグラフ
# install.packages("ggplot2")
library(ggplot2)
autoplot(f_nn_lynx2)
結果はこちら。
参考文献
|
パターン認識と機械学習 上 機械学習法を広く解説したとても有名な書籍です。 上巻はそれほど数式も多くなく、統計学入門という雰囲気もあります。 上巻の最後の章がニューラルネットワークの解説です。 |
 |
|
ソフトコンピューティングと時系列解析―ファジイ・ニューロによる予測入門 名前の通り、ニューラルネットワークなどを用いた時系列解析の方法が書かれた本です。このようなテーマの本はとても少ないため貴重です。 ファジィ理論についても記載があり、こちらも参考になりました。 |
 |
|
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装 深層学習の本ですが、ニューラルネットワークの基礎についても載っています。 パーセプトロンから始まり、丁寧にその発展形としてのニューラルネットワーク、ディープラーニングを解説している本です。おすすめ。 |
 |
スポンサードリンク