2017年5月28日 / 最終更新日時 : 2018年7月7日馬場真哉 Pythonデータ分析

Pythonによる時系列分析の基礎

Pythonを使った時系列解析の方法について説明します。
時系列データの読み込みから、図示、自己相関などの統計量の計算といった基礎から始めて、自動SARIMAモデル推定までを説明します。
この記事を読めば、簡単なBox-Jenkins法についてはPythonで実装する方法が身につくかと思います。

JupyterNotebookでの実行結果はリンク先から確認できます。

スポンサードリンク

1．時系列分析とは

時系列分析とは、その名の通り、時系列データを解析する手法です。
時系列データとは、例えば「毎日の売り上げデータ」や「日々の気温のデータ」、「月ごとの飛行機乗客数」など、毎日（あるいは毎週・毎月・毎年）増えていくデータのことです。
時系列データには「昨日の売り上げと今日の売り上げが似ている」といった関係性を持つことがよくあります。
そのため、時系列データをうまく使えば、昨日の売り上げデータから、未来の売り上げデータを予測することができるかもしれません。

時系列解析を学ぶことで、過去から未来を予測するモデルを作成することができます。

R言語を使った時系列分析の考え方については『時系列解析_理論編』や『時系列分析_実践編』を参照してください。

ここでは、人気のPythonを使った時系列分析の方法、ひいてはモデル化を通した将来予測の方法について説明します。
なお、この記事では、ARIMAモデルを主としたBox-Jenkins法のみを取り扱います。ARIMAモデルとは何か、といったことが知りたければ『時系列解析_理論編』を参照してください。

またPythonやJupyterNotebookの使い方がよくわからないという方は『Pythonの簡単な使い方』を参照してください。Anacondaのインストールは済んでいるという前提で解析を進めていきます。

なお、今回の解析は、以下の条件で実行しました。
OS：Windows
Pythonのバージョン：Python 3.6.0 :: Anaconda custom (64-bit)

2．時系列データの読み込み

Jupyter NoteBookの計算結果はこちらに載せてあります。

まずは、必要となるライブラリを一気に読み込みましょう。

★2018年7月7日追記
sns.set()を追加しました。これによりseabornを用いたグラフの装飾が自動で行われます。

# 基本のライブラリを読み込む
import numpy as np
import pandas as pd
from scipy import stats

# グラフ描画
from matplotlib import pylab as plt
import seaborn as sns
%matplotlib inline
sns.set()

# グラフを横長にする
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 15, 6

# 統計モデル
import statsmodels.api as sm

今回は、月ごとの飛行機の乗客数データを対象とします。期間は1949年1月から1960年12月までです。
初出は「Box, G. E. P., Jenkins, G. M. and Reinsel, G. C. (1976) Time Series Analysis, Forecasting and Control. Third Edition. Holden-Day. Series G.」となります。
以下のURLから、データの詳細を確認できます（R言語の記事です）
https://stat.ethz.ch/R-manual/R-devel/library/datasets/html/AirPassengers.html

R言語では組み込みデータセットとして用意されているのですが、Pythonだと見当たらなかったので、CSVファイルから読み込みます。
以下のサイトにファイルがあったので、それを使いました。
なお、このサイトにもPython時系列分析のコードが載っており、大変参考になりました（英語ですが）。

A comprehensive beginner’s guide to create a Time Series Forecast (with Codes in Python)

ダウンロードする対象のファイルのリンクも張っておきます（外部サイトです）
AirPassengers

なお、このデータの1列目は日付です。そのためExcelなどで開いてから保存すると、よくわからない形式に変換されてしまうので気を付けてください。ファイルを開く場合は、メモ帳などのテキストエディタを使うようにしてください。

それでは、データを読み込みましょう。
まずは普通の読み込み方です。

# 普通にデータを読み込む
# https://stat.ethz.ch/R-manual/R-devel/library/datasets/html/AirPassengers.html
dataNormal = pd.read_csv('AirPassengers.csv')
dataNormal.head()

データを読み込むことはできるのですが、このやり方だと1列目も「データ」として扱われてしまいます。
1列目は単なる日付です。
なので「1列目は日付のインデックスなのだ」と指定をして読み込む必要があります。
また、後ほどSARIMAモデルなどを推定するのですが、このとき、データがint型（整数）のままだとエラーとなってしまいます。
そこで、以下のように読み込みます。

# 日付形式で読み込む（dtype=floatで読み込まないと、あとでARIMAモデル推定時にエラーとなる）
dateparse = lambda dates: pd.datetime.strptime(dates, '%Y-%m')
data = pd.read_csv('AirPassengers.csv', index_col='Month', date_parser=dateparse, dtype='float')
data.head()

★2018年7月7日追記
単純な日付形式だった場合は、以下のように読み込む方が簡単です。

# 以下のコードの方が読み込みは簡単
data = pd.read_csv('AirPassengers.csv', 
                   index_col='Month', 
                   parse_dates=True, 
                   dtype='float')
data.head()

JupyterNotebookの結果を見ていただいた方がわかりよいと思いますが、1列目がただの日付のインデックスになっています。
データは月単位なのですが、それに日数を追加しています（すべて1日目だということにしています）。こうすることで、日付として扱いやすくなります。

1列だけのデータとなりましたので、わざわざデータフレームで持っておく必要もありません。
乗客数のSeriesだけを取り出して「ts」という名前の変数に格納します。
以降は、この「ts」という変数を使って解析を進めていきます。

# 日付形式にする
ts = data['#Passengers'] 
ts.head()

3．時系列データの取り扱い

この節の計算結果はリンク先から見ることができます。

まずは、データをプロットします。
グラフを描かなければ、データ分析は始まりません。

以下の1行でプロットできます。

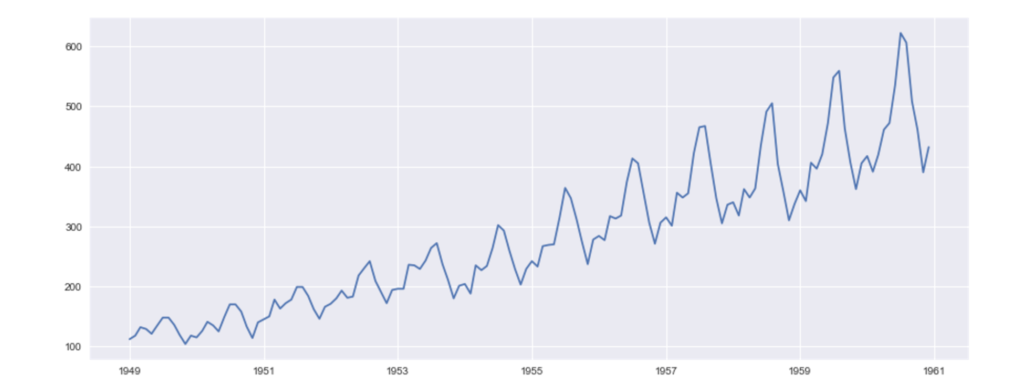
plt.plot(ts)

グラフを描くと、それだけでいろいろなことがわかります。
まずは、乗客数が年々増えているということ。
それから、季節ごとに乗客数が周期的に変わりそうだということ。

季節変動の有無などは後ほどモデル化するのですが。まずは時系列データの取り扱いに慣れていきましょう。

特定の年月のデータを取得する場合は、以下のようにします。

# データの取得方法その1
ts['1949-01-01']

# データの取得方法その2
from datetime import datetime
ts[datetime(1949,1, 1)]

# 1949年のデータをすべて取ってくる
ts['1949']

3種類のデータの取得方法をまとめて載せました。
各々の結果はリンク先も併せて見てみてください。

1つ目と2つ目は同じ結果となります。
各々1949年の1月のデータのみが取得されます。

面白いのは3つ目の方法で、年だけを指定すると、その1年間のデータすべて、すなわち月単位データなので12個のデータが取得されます。

次はデータのシフトと差分のとり方です。
シフトとは、文字通り「データをずらす」ことを指します。データをずらすことで、データの差分を簡単にとることができるようになります。
例えば1949年の2月は1月に比べてどれほど乗客数が増えたのか、を調べたい場合は、差分をとればよいです。
また時系列解析の場合は、対数差分をとることも多くあります。
対数差分は近似的に「変動率」を表す指標となります。また対数をとることでデータがモデルにフィットしやすくなるというメリットもあります。
今回は対数差分系列は使いませんが、その計算方法だけ確認しておいてください。

シフト演算、差分、対数差分の計算の仕方をまとめて載せます。

シフトは『shift()』関数を適用します。

ts.shift()

頭だけ取り出すとこんな感じ。

ts.shift().head()

結果はこちら。

Month 1949-01-01 NaN 1949-02-01 112.0 1949-03-01 118.0 1949-04-01 132.0 1949-05-01 129.0 Name: Passengers, dtype: float64

差分は、シフトする前から、シフトした後を引けばいいです。

diff = ts – ts.shift()
diff.head()

結果はこちら

Month 1949-01-01 NaN 1949-02-01 6.0 1949-03-01 14.0 1949-04-01 -3.0 1949-05-01 -8.0 Name: Passengers, dtype: float64

★2018年7月7日追記
差分系列は以下のようにdiff関数を使うと、より簡単に得られます。

# こちらの方が簡単
ts.diff().head()

結果は同じなので省略します。

対数差分は、単に対数をとってから差分するだけです。

logDiff = np.log(ts) – np.log(ts.shift())

結果に「NaN」が出ているのが気になる場合は、以下のように『dropna」関数を適用します。

logDiff.dropna()

4．自己相関係数の推定

前期と今期がどれだけ似ているか、を表すのが「自己相関」です。
正の自己相関があれば、先月の乗客数が多ければ、今月も多いということがわかります。
負の自己相関であれば、その逆です。

ただ、自己相関だけではやや解釈が難しくなることがあります。
例えば、正の自己相関を持っていたとしましょう。
すると「昨日と今日が似ている」ということに加えて「一昨日と昨日が似ている」という状況になるでしょう。
すると「一昨日と今日」は似ているのでしょうか、それともあまり似ていないのでしょうか。ちょっと判別が難しくなります。
そこで「ほかの日は無視して、特定の日のみとの自己相関が見たい」というニーズが生まれます。
これができるのが『偏自己相関』です。先ほどの例だと「一昨日と昨日が似ている」というのを無視して、純粋に「一昨日と今日の関係」を調べることができます。

# 自己相関を求める
ts_acf = sm.tsa.stattools.acf(ts, nlags=40)
ts_acf

# 偏自己相関
ts_pacf = sm.tsa.stattools.pacf(ts, nlags=40, method='ols')
ts_pacf

結果は長いので、リンク先を参照してください。

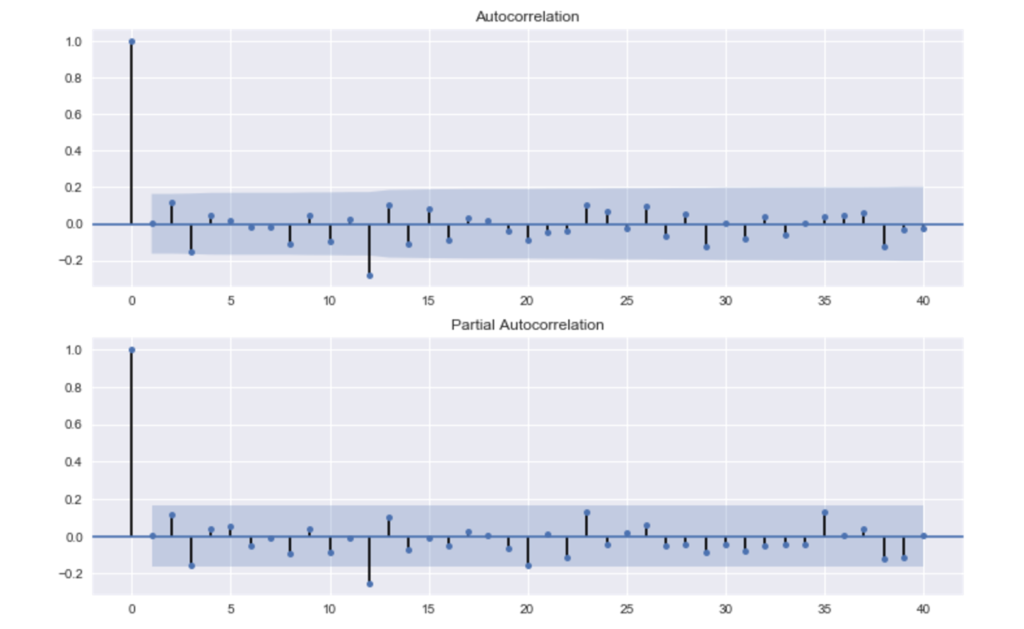
自己相関のグラフを描くこともできます。

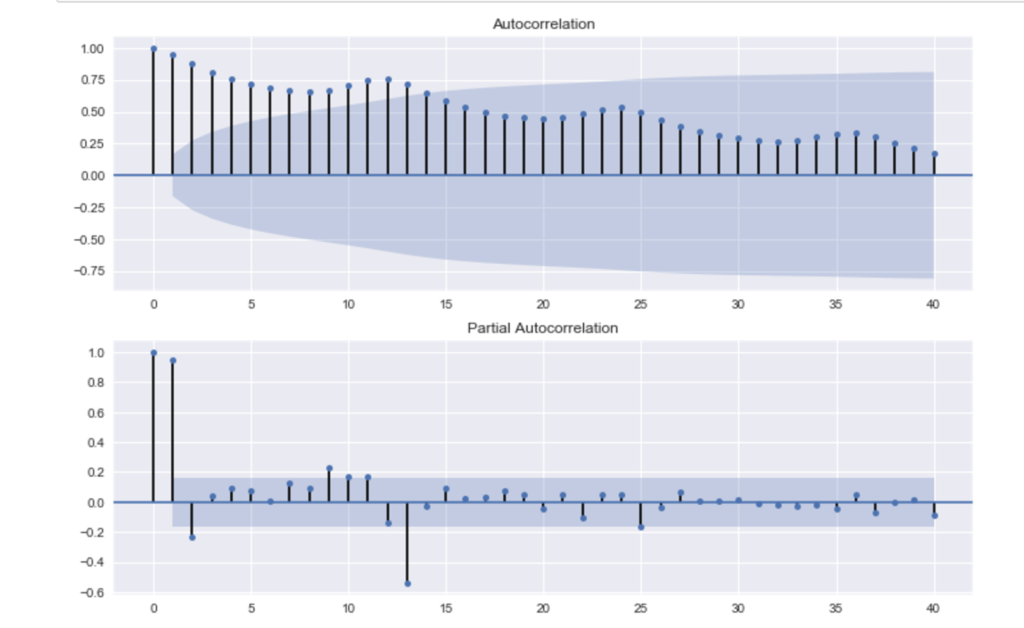
#  自己相関のグラフ
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(ts, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(ts, lags=40, ax=ax2)

偏自己相関のグラフ（2つ目のグラフ）を見ると、やはり12か月周期のそうかんがはっきりとみられます。
季節的な周期変動があることがわかります。
また、前月の乗客数が多ければ、当月も多くなることもグラフからわかります。

スポンサードリンク

5．ARIMAモデルの推定

続いて、モデル化をしましょう。
まずは一般的なARIMAモデルを推定します。
ARIMAモデルの何たるかは『時系列解析_理論編』を参照してください。
とりあえず標準的な時系列モデルです。

Pythonだと、自動でARMAの次数を決めてくれる関数はあるのですが、なぜか「ARMA」の次数しか決めてくれません。
すなわち、何回差分をするか、ということは自動では決めてくれない。

まあ、今回のデータはぱっと見で和分過程っぽいので、差分をとってから解析をすることとします。
差分をとるかどうかの判断については、最後の「自動SARIMAモデル推定」の節で改めて議論します。
結論から言うと、自分でforループを回して最適な次数を調べてやらなくてはなりません。

ここでは、決め打ちで1回差分をしてから、自動AMRA次数決定関数を適用することとします。

まとめてコードを載せます。

# たぶん和分過程なので、差分をとる
diff = ts - ts.shift()
diff = diff.dropna()

# 差分系列への自動ARMA推定関数の実行
resDiff = sm.tsa.arma_order_select_ic(diff, ic='aic', trend='nc')
resDiff

差分系列の作成に関しては説明済みなので省略します。dropnaで邪魔なNaNを消していることだけ注意してください。

『arma_order_select_ic』という関数を使うことで、ARMAの次数を決定できます。
引数としては、対象データ、情報量規準として何を使うか（ほかにはBICなどが使えます）、そしてトレンドの有無です。

原系列にはトレンドがありそうだったのですが、差分をとるとぱっと見、トレンドがなさそうだったので、今回は入れていません（本来は「ぱっと見」ではなくちゃんと確認しないといけないです。念のため）

細かい結果はリンク先を見ていただくとして、とにかく『’aic_min_order’: (3, 2)』という結果が得られます。
ARMA(3,2)が最も良いということとなりました。

最適な次数が分かったので、それでモデルを組みなおします。

# P-3, q=2 が最善となったので、それをモデル化
from statsmodels.tsa.arima_model import ARIMA
ARIMA_3_1_2 = ARIMA(ts, order=(3, 1, 2)).fit(dist=False)
ARIMA_3_1_2.params

結果はこちら

const 2.673501 ar.L1.D.#Passengers 0.261992 ar.L2.D.#Passengers 0.367827 ar.L3.D.#Passengers -0.363472 ma.L1.D.#Passengers -0.075005 ma.L2.D.#Passengers -0.924805 dtype: float64

ただ、このモデルには実は欠点があります。
周期的な季節変動をうまくモデル化できていないのです。

残差の自己相関を見ると、一目瞭然です。

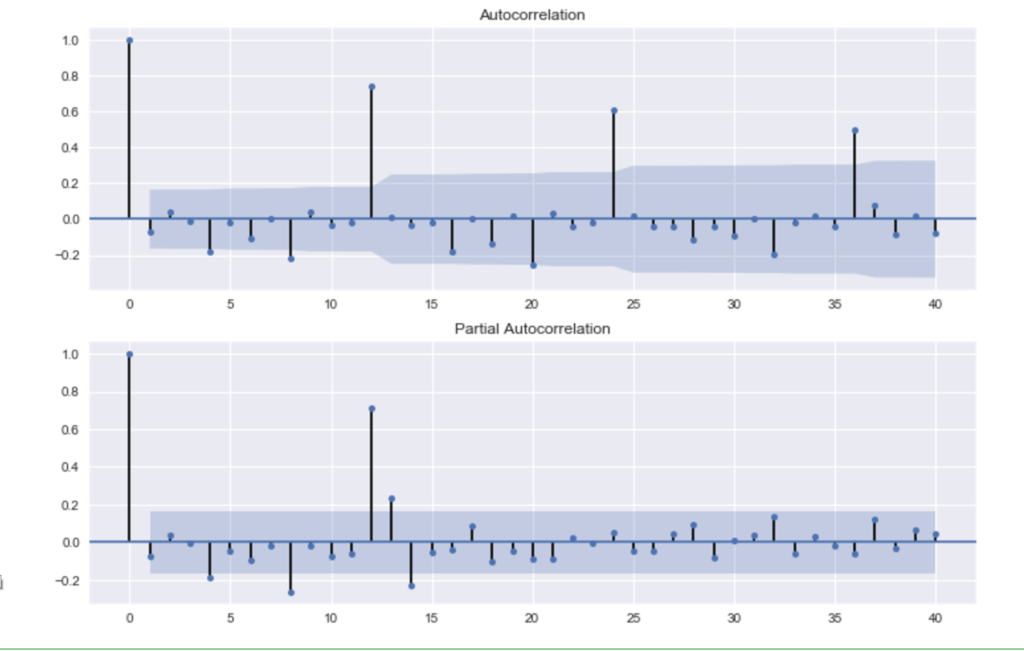
# 残差のチェック
# SARIMAじゃないので、周期性が残ってしまっている。。。
resid = ARIMA_3_1_2.resid
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax2)

12か月周期で、ピョコンピョコンと高い自己相関が残差に現れていることに注意してください。
これではだめだ、ということで、季節変動ありのARIMA、すなわちSARIMAモデルを使うこととなります。

6．SARIMAモデルの推定

計算結果はリンク先を参照してください。

SARIMAモデルを推定する前に、注意点があります。
SARIMAモデルは「statsmodels」というライブラリを使って計算するのですが、こいつのバージョン0.8.0以上でなければSARIMAモデルが入っていません。
SARIMAモデルを推定しようとして「そんな計算はできません」とPythonに怒られた場合は、statmodelsのバージョンを上げてください。

WindowsでAnacondaを使用している場合は、コマンドプロンプトを起動して、以下のコマンドを実行すればOKです。

conda install -c taugspurger statsmodels=0.8.0

準備ができたので、SARIMAモデルを推定します。
季節変動については、次数は決め打ちとします。

# SARIMAモデルを「決め打ち」で推定する
import statsmodels.api as sm

SARIMA_3_1_2_111 = sm.tsa.SARIMAX(ts, order=(3,1,2), seasonal_order=(1,1,1,12)).fit()
print(SARIMA_3_1_2_111.summary())

『SARIMAX』という関数を使います。
名前に「X」が入っているのですが、これは回帰分析のように「外部のほかの変数もモデルに組み込むことができる」ということを意味しています。
今回は一変数のみで行きます。

order=(3,1,2)でARIMAモデルの次数を、seasonal_order=(1,1,1,12)で季節変動の次数を設定します。
seasonal_order=(1,1,1,12)の最後の「12」は「12か月周期」であることを意味しています。なので、実質は(sp,sd,sq)=(1,1,1)です。

結果はこちら。
計算中に、最尤法の結果が収束していないという旨のワーニングが出てしまったのですが、とりあえず無視して先に進みます。

                                 Statespace Model Results                                 
==========================================================================================
Dep. Variable:                         Passengers   No. Observations:                  144
Model:             SARIMAX(3, 1, 2)x(1, 1, 1, 12)   Log Likelihood                -502.990
Date:                            Sat, 27 May 2017   AIC                           1021.980
Time:                                    18:50:26   BIC                           1045.738
Sample:                                01-01-1949   HQIC                          1031.634
                                     - 12-01-1960                                         
Covariance Type:                              opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1          0.5383      1.665      0.323      0.747      -2.725       3.802
ar.L2          0.2830      0.969      0.292      0.770      -1.617       2.183
ar.L3         -0.0346      0.407     -0.085      0.932      -0.832       0.762
ma.L1         -0.9231      1.690     -0.546      0.585      -4.236       2.390
ma.L2         -0.0519      1.658     -0.031      0.975      -3.302       3.198
ar.S.L12      -0.8773      0.285     -3.077      0.002      -1.436      -0.318
ma.S.L12       0.7839      0.370      2.116      0.034       0.058       1.510
sigma2       124.6735     14.315      8.709      0.000      96.616     152.731
===================================================================================
Ljung-Box (Q):                       51.03   Jarque-Bera (JB):                13.51
Prob(Q):                              0.11   Prob(JB):                         0.00
Heteroskedasticity (H):               2.60   Skew:                             0.14
Prob(H) (two-sided):                  0.00   Kurtosis:                         4.55
===================================================================================

まず目を引くのが「Statespace Model Results」というヘッダーです。
お前、いつの前に状態空間モデルが出てきたんだよ、という感じなのですが、どうも内部でパラメタ推定にカルマンフィルタを使っているようです。
状態空間モデルを使うことでBox-Jenkins法を統一的に取り扱うことができます。実際の計算にもこれを使っているのでしょう。

summaryの結果には、AICなどの情報量規準の一覧に加え、推定された係数も表示されています。
完ぺきな結果かといわれると、残念ながらそうではなさそうですが、とりあえずこのまま進めます。

残差の自己相関については、ほぼ問題なくなったでしょう。

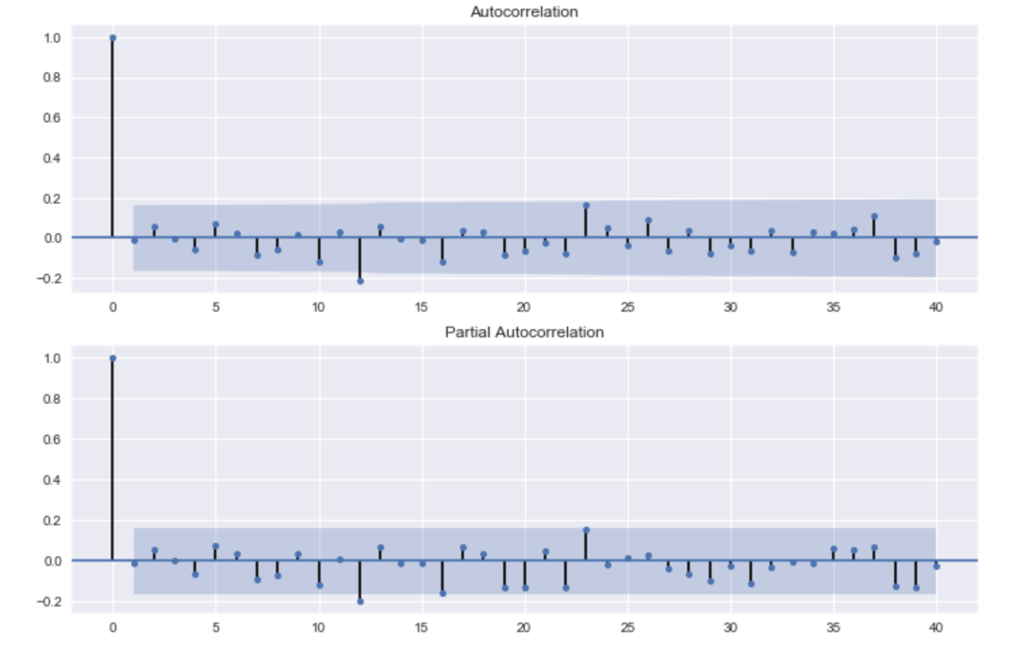
# 残差のチェック
residSARIMA = SARIMA_3_1_2_111.resid
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(residSARIMA.values.squeeze(), lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(residSARIMA, lags=40, ax=ax2)

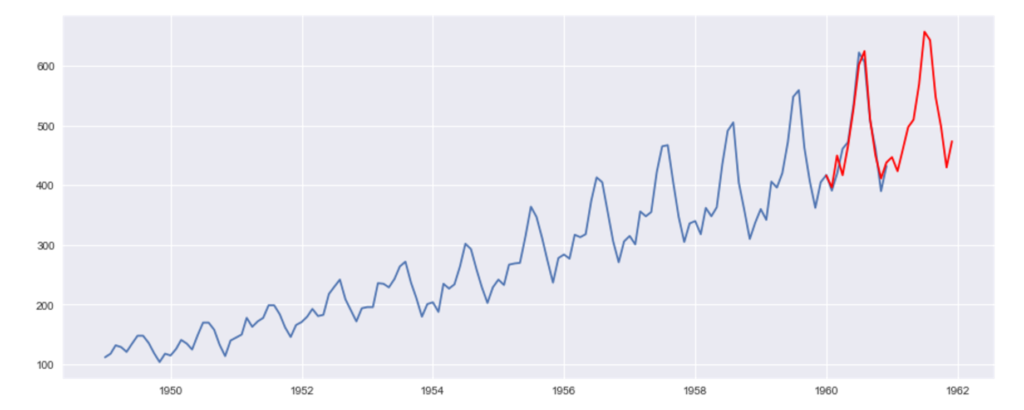
モデルが組めたので、予測をしてみます。

# 予測
pred = SARIMA_3_1_2_111.predict('1960-01-01', '1961-12-01')

# 実データと予測結果の図示
plt.plot(ts)
plt.plot(pred, "r")

予測にはそのまま『predict(予測開始日, 予測終了日)』関数を使うのですが、予測対象となる日付は「もともとのサンプルに含まれていた日付」からスタートする必要があることに注意してください。
データは1960年12月まであります。将来を予測したいのだから、1961年の1月スタートで予測したくなるのですが、そうするとエラーになります。

予測結果はこちら。
周期性も併せて予測ができました。

7．総当たり法によるSARIMAモデル次数の決定

実行結果はリンク先を参照してください。

最後に、SARIMAモデルの次数を決定する自作のプログラムを書いてみます。
やることは総当たりで次数を変えていき、AICを計算し、比較をしていくだけなのですが、いくつかはまりポイントがあったので、共有できればと思います。

まずは、AICを格納する入れ物を用意します。
最大次数を決めておけば、何パタンのモデルが作られるかを計算して求めることができるので、あらかじめ繰り返し数を求めておき、その分だけ行数を確保します。

次数に関しては、以下のルールで表記します。
ARIMA(p, d, q)
季節(sp, sd, sq)
各々、
pは自己回帰モデルの次数：AR(p)、
qは移動平均モデルの次数：MA(q)、
dは差分をとる回数：I(d)
です。

# 総当たりで、AICが最小となるSARIMAの次数を探す
max_p = 3
max_q = 3
max_d = 1
max_sp = 1
max_sq = 1
max_sd = 1

pattern = max_p*(max_q + 1)*(max_d + 1)*(max_sp + 1)*(max_sq + 1)*(max_sd + 1)

modelSelection = pd.DataFrame(index=range(pattern), columns=["model", "aic"])
pattern

これを実行すると、パターンの数は「192」となります。すなわち192回繰り返しSARIMAモデルを推定するということです。
最大次数を「３」にしたのは、ただの経験則です。これを増やすと、それだけ多くの時間がかかってしまう点だけ注意してください。
季節の次数に関しては、大きくならないイメージがあるので、小さめにとっています。
コンピュータの資源に自信がある方は、もっと大きな数値を設定してください。

なお、patternの数の計算式（９行目）においてmax_pだけプラス1されていませんが、これは誤植ではありません。
ARIMAモデルのAR項の次数を０にして実行すると、エラーが頻発してしまったため、あえてAR項は「最低次数は１とする」という条件でループさせています。
そのため、このようなやや歪な回数だけ計算を実行させることになります。

実際にSARIMAモデルを推定するコードはこちらです。
ひたすらループを回すだけです。

# 自動SARIMA選択
num = 0

for p in range(1, max_p + 1):
    for d in range(0, max_d + 1):
        for q in range(0, max_q + 1):
            for sp in range(0, max_sp + 1):
                for sd in range(0, max_sd + 1):
                    for sq in range(0, max_sq + 1):
                        sarima = sm.tsa.SARIMAX(
                            ts, order=(p,d,q), 
                            seasonal_order=(sp,sd,sq,12), 
                            enforce_stationarity = False, 
                            enforce_invertibility = False
                        ).fit()
                        modelSelection.ix[num]["model"] = "order=(" + str(p) + ","+ str(d) + ","+ str(q) + "), season=("+ str(sp) + ","+ str(sd) + "," + str(sq) + ")"
                        modelSelection.ix[num]["aic"] = sarima.aic
                        num = num + 1

pythonは中カッコを使わず、インデントでループなどを表現するのですが、ここまで多くのループを入れ子にすると、ちょっと読みづらいですね。

ここで注意してほしいのは、SARIMAX関数の中で使われている引数です。
13，14行目に各々『enforce_stationarity = False』『enforce_invertibility = False』という指定をしています。
これがないとエラーがたくさん出てきて、ループを回すどころではなくなるので注意してください。

和分過程に対して、普通の自己回帰モデルなどを適用する際に「定常過程のモデルを推定しなければならない → enforce_stationarity = True」を指定していると、そもそもモデルが推定できませんね。
普通は和分過程を相手にする場合は、必ず差分をとってから自己回帰モデルを適用するのですが、今回は次数を総当たりで変えているため、「和分過程に自己回帰モデルを適用する」という計算が行われてしまいます。
そこでエラーをなくすために無理やりこんな指定をしています。
普通は「和分過程に自己回帰モデルを適用」したような結果が選ばれることはないのですが、AIC最小だからといって手放しにそれを採用するのではなく、「まともな」次数になっているかどうかを確認してから使うようにしてください。

なお「enforce_invertibility」は移動平均モデルの反転可能条件を維持するかどうかの指定です。これもFalseにしないとエラーだらけになります。

また、エラーは出なくなったものの、パラメタ推定の結果が「収束していない」というワーニングが大量に出てきます。

★2017年5月28日追記
コードの15行目、モデルをフィットさせる際、以下のように最適化の方法を変更＋繰り返し数を増加させると、ワーニングの数を減らすことができました。
それでもすべてではなく、いくつかはワーニングが出ます。
fit(method=’bfgs’, maxiter=300, disp=False)

選ばれた結果は過剰に信用するのではなく、ある程度疑ってかかりながら解析を進めるしかないかと思います。

数分で結果が出てきます。
AIC最小モデルを拾ってくると、こうなります。

# AIC最小モデル
modelSelection[modelSelection.aic == min(modelSelection.aic)]

　　　　model　　　　　　　　　　　　　　　　aic
187　　order=(3,1,3), season=(0,1,1)　　　898.105

order=(3,1,3), season=(0,1,1)がAIC最小モデルとなったので、この次数を使ってもう一度SARIMAモデルを組みなおします。

#
#
bestSARIMA = sm.tsa.SARIMAX(ts, order=(3,1,3), seasonal_order=(0,1,1,12), enforce_stationarity = False, enforce_invertibility = False).fit()

print(bestSARIMA.summary())

結果はこちら。

                                 Statespace Model Results                                 
==========================================================================================
Dep. Variable:                         Passengers   No. Observations:                  144
Model:             SARIMAX(3, 1, 3)x(0, 1, 1, 12)   Log Likelihood                -441.052
Date:                            Sat, 27 May 2017   AIC                            898.105
Time:                                    18:53:24   BIC                            921.863
Sample:                                01-01-1949   HQIC                           907.759
                                     - 12-01-1960                                         
Covariance Type:                              opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1         -0.2231      0.097     -2.302      0.021      -0.413      -0.033
ar.L2         -0.1642      0.108     -1.515      0.130      -0.377       0.048
ar.L3          0.7244      0.094      7.704      0.000       0.540       0.909
ma.L1         -0.0837    121.897     -0.001      0.999    -238.997     238.829
ma.L2          0.1221    152.640      0.001      0.999    -299.046     299.290
ma.L3         -0.9797    266.561     -0.004      0.997    -523.429     521.469
ma.S.L12      -0.1583      0.118     -1.337      0.181      -0.390       0.074
sigma2       119.6719   3.26e+04      0.004      0.997   -6.37e+04    6.39e+04
===================================================================================
Ljung-Box (Q):                       36.68   Jarque-Bera (JB):                 4.39
Prob(Q):                              0.62   Prob(JB):                         0.11
Heteroskedasticity (H):               1.87   Skew:                             0.16
Prob(H) (two-sided):                  0.06   Kurtosis:                         3.90
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

残差も、大きくは支障なさそうです。

# 残差のチェック
residSARIMA = bestSARIMA.resid
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(residSARIMA, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(residSARIMA, lags=40, ax=ax2)

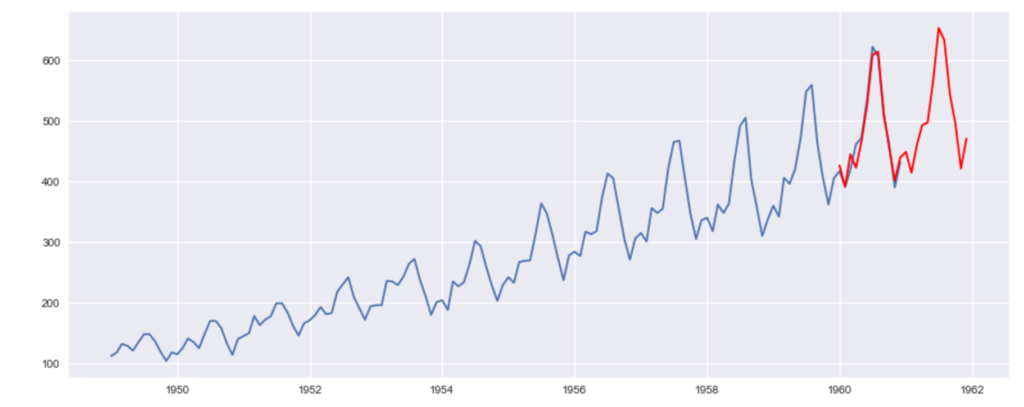
最後は予測です。

# 予測
bestPred = bestSARIMA.predict('1960-01-01', '1961-12-01')
# 実データと予測結果の図示
plt.plot(ts)
plt.plot(bestPred, "r")

駆け足ではありましたが、Pythonを使って、簡単な時系列モデルを構築～予測を出すところまで一通り流すことができました。

Pythonでの時系列分析に関する日本語の資料が少なくて、やや難儀しました。
もっとこうしたほうがいい、などのご意見があれば、メールやコメントなどいただければ幸いです。

WebでPythonを学ぶなら

実践 Python データサイエンス

動画でPythonやJupyter Notebookの使い方を学ぶことができる勉強サイトです。
Udemyを利用すると、Pythonやデータ分析を「基礎から順にステップアップする内容で、かつ動画で」学ぶことができます。
ネットで受ける通信教育、みたいな感じです。
管理人も受講してみました。体験記はこちらから読めます。

参考文献

時系列分析と状態空間モデルの基礎：
RとStanで学ぶ理論と実装

管理人の書いた時系列分析の入門書です。
時系列分析のイロハのイから解説しました。
サポートページはこちらです。目次なども公開されています。

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)

このサイトで時系列解析関連の記事を書く際は必ず参照している本です。
時系列解析の基本となる考え方から始めて、モデルの詳しい説明まで載っています。
今、時系列解析を学びたいと思った方はこの本から入ると良いでしょう。

Think Stats 第2版 ―プログラマのための統計入門

Pythonでデータ分析をするための入門書です。統計学の理論に関する説明は少なめですが、とりあえずコードを書いて勉強したいという場合に良いかと思います。
時系列分析も1章載っていますが、ARIMAモデルの説明はありません。

書籍以外の参考文献

・Statsmodels Examples
　→計算例一覧が載っています

・Autoregressive Moving Average (ARMA): Sunspots data
　→太陽黒点に対してARMAモデルを適用した計算例

・statsmodels.tsa.statespace.sarimax.SARIMAX
　→SARIMAX関数の説明

・A comprehensive beginner’s guide to create a Time Series Forecast (with Codes in Python)
　→今回最も参考になった外部サイトです。解析の手順が載っています。SARIMAの解説はないですが。

スポンサードリンク