階層分析法「AHP」の考え方とPythonによる実装

AHP(Analytic Hierarchy Process：階層分析法)は、2つ以上の評価基準がある中で意思決定を行う方法の1つです。例えば、安い代わりに品質が悪い製品と、価格は高いが品質の良い製品の、どちらを購入するかを考える時などに使われます。

この記事では AHPの基本的な理論を説明したうえで、Pythonでこれを実装する方法を説明します。
実装の際はsympyという数値計算ライブラリを用います。
分析コードはGitHubで管理しています。完全なコードはこちらで公開しています。

スポンサードリンク

目次

1. AHPとは
2. 「2つの基準・2つの選択肢」の例
   1. 今回扱う事例
   2. 直観的な考え方
   3. 「重み」に基づく判断
   4. 1対比較による比較行列の作成
   5. 比較行列と重みの関係
   6. 比較行列の固有ベクトルを計算して重みを得る
   7. 「2つの基準・2つの選択肢」のAHPのまとめ
3. Pyhonで計算するAHP
   1. 味と価格の2つの基準の重みを計算する
   2. 比較行列から重みを計算するための関数を作る
   3. 寿司と牛丼問題を解決する
4. 3つ以上の比較と比較行列の一貫性
   1. 比較行列の一貫性
   2. 推移性規則が満たされている例
   3. 推移性規則が満たされていない例
   4. 一貫性の評価
   5. Pythonによる一貫性の評価
   6. 寿司と牛丼、ラーメン問題を解決する

 

1．AHPとは

AHPは、2つ以上の評価基準がある中で意思決定を行う方法の1つです。例えば、安い代わりにあまりおいしくない料理と、価格は高いがとてもおいしい料理の、どちらを食べるかを考える時などに使われます。

2つ以上の評価基準がある、と言うと複雑に見えます。しかしAHPの目指すことは単純です。
まずは、価格と品質のどちらの基準を重要視するかを先に決めます。
そして「重要視する基準」が高い選択肢を採用します。

当たり前のことを、と思われるかもしれませんが、この手続きを標準化して、比較的簡単に計算できるように整理したことの功績は大きいと思います。

 

AHPはAnalytic Hierarchy Processの略で、日本語にすると階層分析法となります。複雑な意思決定であっても、階層を分けることで、1つ1つは機械的な手続きで意思決定ができるように工夫されています。

レベル1の階層は「意思決定の目的」です。
どの料理を選ぶか、どの商品を選ぶか、どの会社に就職するか、新しいプロジェクトとしてどのようなものを立ち上げるか。こういったものが意思決定の目的となります。
例えば、休日のランチとして、どのお店に行くかを決めることを目的とします。

レベル2の階層は「基準」です。
味という基準であったり、価格という基準などが想定されます。

レベル3の階層は「選択肢」です。
例えば、お寿司屋さんや牛丼屋さんなど、候補となるお店が列挙されます。

 

2．「2つの基準・2つの選択肢」の例

通常の教科書だと、3つ以上の基準・選択肢の例が扱われることが多いのですが、これだと考慮すべき事柄が多いので、少し難しいです。
この記事では、まず「2つの基準・2つの選択肢」という、とても単純な事例を確認してから、複雑な分析に移ることにします。

 

今回扱う事例

目的

休日のランチとして、どのお店に行くかを決める

基準

• 味
• 価格

選択肢

• 寿司屋
• 牛丼屋

 

直観的な考え方

まずは優先させたい基準が何なのかを判断します。
例えば「味を優先したいな」と思ったとします。

続いて、選択肢ごとに、基準の優劣を評価します。以下のようになったとします。
寿司屋：味は良いが、価格が高い
牛丼屋：味は悪いが、価格が安い

価格は安い方が良く、高いのは悪いという評価となります。

最終的には「味を優先してお店を決めたいので、お寿司屋に行こう」と決めることになります。
 

補足しておくと「味を優先したいな」というのは個人の好みです。私が味を優先させたいと思ったからと言って、ほかの人がそう思うかはわかりません。
あくまでも個人、あるいは単一の組織の行動を決めているのだと、ご理解ください。
今回は「寿司屋の方が味が良い」としましたが、これも好みの問題でしょう。牛丼の味の方が好きな人もいるはずです。これは、自分が意思決定をする場合には自分の心に尋ねるしかありません。相手の意思決定を支援する場合は、相手にアンケートをとって確認しておく必要があります。大変にどうでもよいですが、私自身は牛丼が大好きです。

価格に関しても、人によって価値観が異なるので注意が必要です。
例えば、私なんかだと貧乏性なので、1000円のランチと1500円のランチだと、結構な差があると感じます。でも、高給取りな方ですと、500円の差なんて気にもしないかもしれませんね。5000円以上の差が出てきて、初めて金額で優劣がつく、なんてこともあるかもしれません。このあたりの感覚は、次節で重みを評価する際に大切になってきます。

 

「重み」に基づく判断

先のやり方は単純ではあるのですが、問題もあります。
「味と価格だと、味の方を”わずかに”優先したい」という場合と「味の方を”圧倒的に”優先させたい」というのは異なるはずです。

例えば「寿司と牛丼なら、圧倒的に牛丼の方が安い」という状況だったとします。
この時「味の優先度が価格よりわずかに勝っているだけ」の場合は、牛丼が選ばれるかもしれません。
逆に「味の優先度が価格より圧倒的に勝っている」という場合は、寿司が選ばれるかもしれません。
どちらを優先するかという順序だけでなく、その度合いを評価することが必要ということです。

AHPでは、基準や選択肢を順序付けるのに「重み」あるいは「優先度」と呼ばれる数値を使います。
例えば
味：価格　＝　３：１
という比率で重みをつけることを考えたとします。重みの合計値を1とすると、味の重みは「0.75」で価格の重みは「0.25」となりますね。
このように数値で評価しておけば、優先の度合いを評価できそうです。

重みの評価ができる場合は、以下の手順で判断することになります。
1．基準の重みを評価する
2．ある1つの基準に対する、選択肢の優先度を評価する
3．すべての基準を考慮して、選択肢の総合優先度を評価する

 

計算例

基準の重み
味の重み　　0.75
価格の重み　0.25
（味：価格＝３：１）

1つの基準に対する、選択肢の優先度

①味という基準に対する優先度
寿司の重み　0.83
牛丼の重み　0.17
（寿司：牛丼＝５：１）

②価格という基準に対する優先度
寿司の重み　0.1
牛丼の重み　0.9
（寿司：牛丼＝１：９）

すべての基準を考慮して、選択肢の総合優先度を評価

以下の計算によって、総合優先度を求めます。
味の重み×（各選択肢の味の優先度）＋価格の重み×（各選択肢の価格の優先度）

寿司の総合優先度
0.75×0.83 ＋　0.25×0.1より
およそ0.65

牛丼の総合優先度
0.75×0.17 ＋　0.25×0.9より
およそ0.35

 
というわけで、総合優先度はお寿司の方が順位が高いという結果になりました。
お寿司を食べに行きましょう。

 

1対比較による比較行列の作成

基準の重みや「各基準に対する、選択肢の優先度」を計算できれば、総合的な評価に基づいて判断が下せそうです。
しかし、今回のような単純な2つの選択肢での比較ならともかくとして、比較対象が3つや4つになってくると、重みや優先度を評価するのが大変となります。
そこで、AHPでは、この作業を簡単にするために、1対比較を通して比較行列を作ります。

1対比較のもたらすご利益は、3つ以上を比較するときに得られます。3つ以上の比較を行う例は、後ほど紹介します。まずは、1対比較と比較行列の作成手順を整理します。

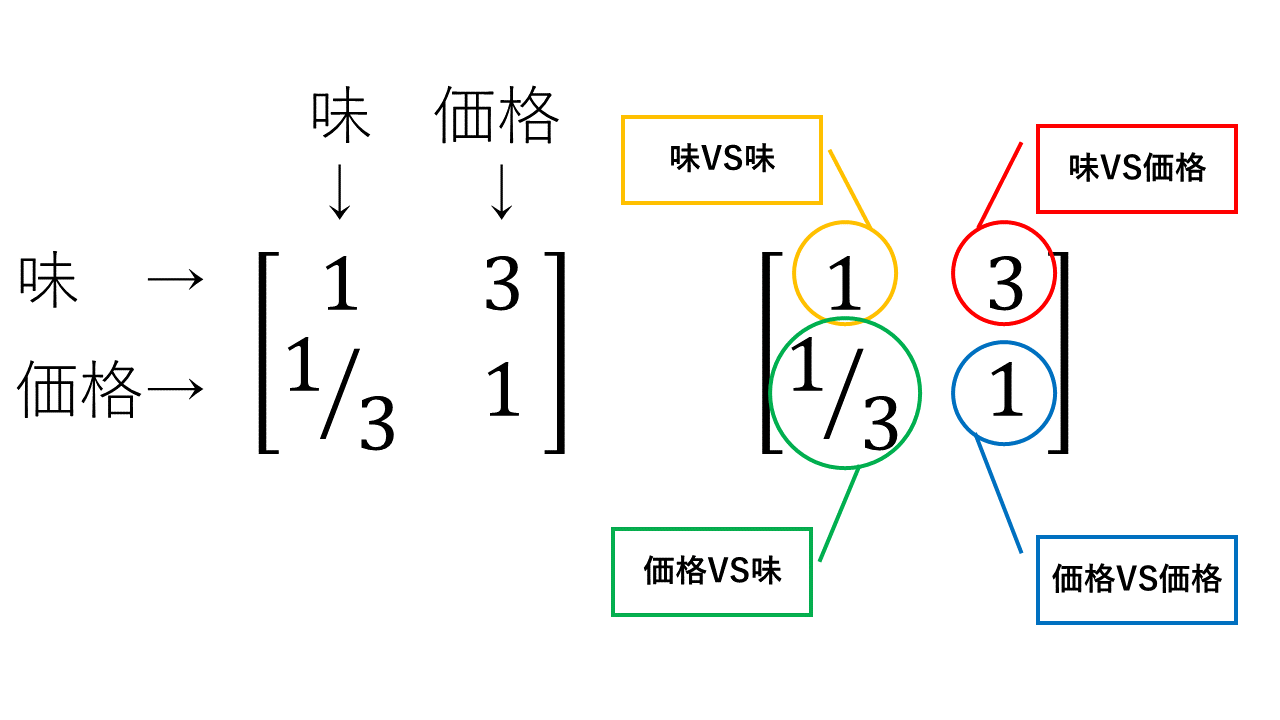
基準として、味・価格の2つがあった時「味VS価格」でその優劣を比較します。
もしも、味・価格・待ち時間の3つの基準があるときは「味VS価格」「味VS時間」「価格VS時間」の3通りの1対比較を行うことになります。
今回は2つしか基準がないことを想定しているので、1回だけ比較すれば完了ですね。

比較の際には、以下の比較尺度を使います。表現は木下(2004)を参考にしました。

言葉による表現	数値尺度
同じくらいに重要	１
やや重要	３
かなり重要	５
非常に重要	７
極めて重要	９

平たく言えば、数値が大きくなればなるほど重要だということです。なお、偶数はなるべく使わないようにします。どうしても中間的な評価をせざるを得ないときには、使うこともあるようです。

 
数値を当てはめていきます。
この時、重要なものの方が数値が大きくなります。
重要ではない方（今回は価格）は、逆数をとって「1/3」となります。

1つめの要素を「味」、2つめの要素「価格」にした時の比較行列Aは以下のようになります。
$$ \boldsymbol{ A } = \left[\begin{matrix}1 & 3\\ 1/3 & 1\end{matrix}\right] $$

 
比較行列のイメージは以下のようになります。

 

比較行列と重みの関係

良く設計された比較行列は、重み成分の比としてあらわすことができます。
「良く設計された」というのは含みを持たせた表現ですが、2つの基準・選択肢での評価においてはあまり気にする必要がないです（だから2つの評価は簡単なのです）。「良くない設計の比較行列」の例は、3つ以上での比較の際に紹介します。

基準の重みは以下のようになっていました。
味の重み　　\( w_1 = 0.75 \)
価格の重み　\( w_2 = 0.25 \)
（味：価格＝３：１）

比較行列の1行1列目は「 \( w_1 \div w_1 = 0.75÷0.75=1 \) 」となります。
比較行列の1行2列目は「 \( w_1 \div w_2 = 0.75÷0.25=3 \)」となります。
比較行列の2行1列目は「 \( w_2 \div w_1 = 0.25÷0.75=1/3 \)」となります。
比較行列の2行2列目は「 \( w_2 \div w_2 = 0.25÷0.25=1 \)」となります。

数式で表記すると以下のようになります。
$$ \boldsymbol{ A } = \left[\begin{matrix} w_1/w_1 & w_1/w_2 \\ w_2/w_1 & w_2/w_2 \end{matrix}\right] $$

「良く設計された比較行列は、重み成分の比としてあらわすことができる」という事実は、後ほど重み成分を計算で得る際に重要になってくるので覚えておいてください。

 

比較行列の固有ベクトルを計算して重みを得る

※ここでは線形代数の知識が要求されますが、難しければ飛ばし読みしても大丈夫です。最終的な計算は、プログラムを書いて行うので、手計算ができなくても大きな問題にはなりません。

良く設計された比較行列においては、その固有ベクトルを重み成分とみなすことができます。厳密にいえば「最大固有値を持つときの固有ベクトル」が「重み成分のベクトル」となります。
固有値と固有ベクトルというのは線形代数で学ぶ専門用語ですね。いろいろと難しいところもありますが、定義だけ理解しておけば、取り急ぎAHPの理解には十分かと思います。

固有値と固有ベクトルの復習

まずは（釈迦に説法かもしれませんが）表記法の整理から進めます。
まず、対象となる行列を\( \boldsymbol{ A } \)とします。行列は大文字で太文字のアルファベットで表記されます。
列数と行数が等しい行列を正方行列と呼びます。比較行列は、（行数も列数も比較対象となるものの個数と一致するので）正方行列となります。

固有ベクトルなどのベクトルは、小文字で太文字のアルファベットで表記されます。今回は2行1列の重みベクトルを求めたいわけです。
$$ \boldsymbol{ w } = \left( \begin{array}{c} w_1 \\ w_2 \\ \end{array}\right) $$
なお、すべての要素が0であるベクトルを零ベクトルと呼びます。

数値の4などは、行列でもベクトルでもありません。「普通の数値」を区別するためにスカラーと呼びます。固有値はスカラーです。

 
固有値・固有ベクトルの定義を見ます。

ある正方行列\( \boldsymbol{ A } \)、零ベクトルでないベクトル\( \boldsymbol{ w } \)、スカラー\( \lambda \)の間に以下の関係が成り立つとき、
\( \boldsymbol{ w } \)を\( \boldsymbol{ A } \)の固有ベクトル、\( \lambda \)を\( \boldsymbol{ A } \)の固有値と呼びます。

$$ \boldsymbol{ A }\boldsymbol{ w } = \lambda \boldsymbol{ w } $$

 

固有ベクトルと重みベクトルの関係

さて、いったん固有値・固有ベクトルは脇に置いておいて、良く設計された比較行列と重みベクトルの関係を確認します。

良く設計された比較行列は、以下のように、重みの比で表すことができます。
$$ \boldsymbol{ A } = \left[\begin{matrix} w_1/w_1 & w_1/w_2 \\ w_2/w_1 & w_2/w_2 \end{matrix}\right] $$

行列の掛け算の公式を思い出すと、比較行列と重みベクトルの積は、以下のように計算されることがわかります。

$$
\boldsymbol{ A }\boldsymbol{ w }
= \left[\begin{matrix} w_1/w_1 & w_1/w_2 \\ w_2/w_1 & w_2/w_2 \end{matrix}\right] \left( \begin{array}{c} w_1 \\ w_2 \\ \end{array}\right)
= \left( \begin{array}{c} w_1 + w_1 \\ w_2 + w_2 \\ \end{array}\right)
= 2 \boldsymbol{ w }
$$

すなわち「比較行列と重みベクトルの積」は「比較対象数（スカラー）と重みベクトルの積」になるわけです。

さて「行列とベクトルの積」が「スカラーとベクトルの積」になるのが固有値と固有ベクトルでした。固有値\( \lambda \)と固有ベクトル\( \boldsymbol{ w } \)は、上記の比較対象数と重みベクトルに対応します。
ところで、比較行列のように行列の要素が正である正方行列は、たった1つの最大固有値を持ち、その時の固有ベクトルの各成分が正になることが証明されています。
というわけで、比較行列\( \boldsymbol{ A } \)における、最大固有値を持つ固有ベクトルを求めると、それを重みベクトルとみなすことができそうだ、ということになるわけですね。

なお、最後に重みの合計値を1にする作業が入ります。
得られた固有ベクトルの各要素を、固有ベクトルの要素の合計値で割ってやれば、重みベクトル完成です。

ここで紹介した重みベクトルの計算方法は、固有値法と呼ばれます。
ほかにも幾何平均を使う方法などいくつかが知られています。

 

「2つの基準・2つの選択肢」のAHPのまとめ

2つの基準（味と価格）と2つの選択肢（牛丼とお寿司）があるときのAHPの流れを見てきました。
基本的な考えは以下の通りです。
1．味と価格では、味の方を優先させたいな
2．牛丼とお寿司では
　　味　：お寿司が勝っている
　　価格：牛丼が勝っている
3．味を優先させたいから、お寿司を食べよう

この流れは直観的かと思います。まずは基準の優先順位を定めてから、そのあとで選択肢の優先順位を決めよう、という階層構造があるわけです。

この次に、『味の方を優先させたいな』という言葉による表現をやめて、重み（優先度）という概念を導入しました。
例えば、「味：価格」では「3：1」の比率で重みをつけよう、といった具合です。この場合は、味の重みが0.75で、価格の重みが0.25となります。
同様に「味に関する、牛丼とお寿司の重み」と「価格に関する、牛丼とお寿司の重み」を得たうえで、重み付きの合計値を計算することで、「味と価格の総合評価」に基づく、選択肢の優先付けができるようになりました。

最後に、重みを計算するための固有値法の説明をしました。
重要さの度合いを「１，３，５，７，９」といった数値で表現し、この結果を使って比較行列を得ました。比較行列において、最大固有値を持つ固有ベクトルを得ることで、重みを機械的に計算することができました。
固有値法による重みの計算は、一見すると複雑で大変そうに見えますが、Pythonなどのプログラミング言語を使うことで、ある程度簡略化できます。

スポンサードリンク

 

3．Pyhonで計算するAHP

固有値や固有ベクトルはPythonのsympyというライブラリを使うことで精度よく計算ができます。
分析コードはGitHubで管理しています。完全なコードはこちらで公開しています。

まずはライブラリを読み込みます。
また『init_printing()』と実行することで、出力が美しくなります。

# ライブラリを読み込む
from sympy import * 

# 出力を美しくする
init_printing()

 

味と価格の2つの基準の重みを計算する

比較行列を作ります。まずは基準を対象とします。sympyで行列を作る際は『Matrix』というクラスを使います。

# 基準の行列
eval_mat_1 = Matrix(    
    [[1   , 3,],
     [1/3 , 1]]
)

固有値や固有ベクトルを得るコードは以下の通りです。
『eigenvects』という関数を使うと、固有値も併せて出力されます。

# 固有値と固有ベクトル
eigen_val_vects_1 = eval_mat_1.eigenvects()
eigen_val_vects_1

結果はこちら。固有値・固有ベクトルが2セット得られます。
本当に、以下で示すように、美しい数式の表現で得られます。sympyは便利ですね。
$$ \left [ \left ( 0, \quad 1, \quad \left [ \left[\begin{matrix}-3.0\\1.0\end{matrix}\right]\right ]\right ), \quad \left ( 2.0, \quad 1, \quad \left [ \left[\begin{matrix}3.0\\1.0\end{matrix}\right]\right ]\right )\right ] $$

 
ちなみに、0番目の要素が固有ベクトルで、1番目の要素が多重度、2番目の要素が固有ベクトルとなっています。
インデックスを忘れてしまわないように保存しておきます。

# 固有値と多重度、固有ベクトルのインデックスを保存しておく
EIGEN_VAL_IDX = 0
MULUTIPLICITY_IDX = 1
EIGEN_VEC_IDX = 2

こうしておけば、例えば以下のようにして、最大固有値とその時の固有ベクトルを取得できます。

# 最大固有値とその時の多重度・固有ベクトルを取得
max(eigen_val_vects_1, key=(lambda x: x[EIGEN_VAL_IDX]))

最大固有値とその時の多重度・固有ベクトルを個別に取得したうえで、固有ベクトルを表示させます。

# 要素ごとに分けて取得
eigen_val, multiplicity, eigen_vec = max(eigen_val_vects_1, key=(lambda x: x[EIGEN_VAL_IDX]))
eigen_vec

$$ \left [ \left[\begin{matrix}3.0\\1.0\end{matrix}\right]\right ] $$

ただ、この固有ベクトルが、なぜかlist形式になっているんですね(sympy 1.3です。『type(eigen_vec)』と実行すれば確認できます)。
これでは不便なので、以下のようにしてlistの最初の要素を取得します。そうすれば、後で計算がやりやすくなります。

# 最初の要素を取得
eigen_vec[0]

$$ \left[\begin{matrix}3.0\\1.0\end{matrix}\right] $$

得られた固有ベクトルを、合計値が1になるように標準化してやれば、重みベクトルが得られます。

# 重みの計算
eigen_vec[0] / sum(eigen_vec[0])

$$ \left[\begin{matrix}0.75\\0.25\end{matrix}\right] $$

 

比較行列から重みを計算するための関数を作る

上記の計算を何度も繰り返すのは面倒なので、関数にまとめます。

# 比較行列から重みベクトルを計算する関数
def calc_ahp_weight_vec(comparison_mat):
    '''
    比較行列から重みベクトルを計算する関数

    Arguments:

    comparison_mat -- 比較行列
    
    '''
    
    # 固有値のインデックス
    EIGEN_VAL_IDX = 0
    
    # sympyの関数を使って、固有値と固有ベクトルを得る
    eigen_val_vects = comparison_mat.eigenvects()
    
    # 最大固有値とその時の多重度・固有ベクトルを取得
    eigen_val, multiplicity, eigen_vec = max(eigen_val_vects, key=(lambda x: x[EIGEN_VAL_IDX]))
    
    # 重みの合計が1になるように標準化
    weight_vec = eigen_vec[0] / sum(eigen_vec[0])
    
    # 重みを返す
    return(weight_vec)

 
関数を作っておけば、以下のようにたった1行のコードで重みを計算できます。

# 確認
calc_ahp_weight_vec(eval_mat_1)

$$ \left[\begin{matrix}0.75\\0.25\end{matrix}\right] $$

 

寿司と牛丼問題を解決する

お寿司と牛丼のどちらを食べるか、という問題を決着させましょう。
まずは、以下の3つの比較行列を用意します。
1．基準の比較行列
2．味に関する、寿司・牛丼の比較行列
3．価格に関する、寿司・牛丼の比較行列

# 基準の行列
# 要素1が味
# 要素2が価格
eval_mat_1 = Matrix(    
    [[1   , 3,],
     [1/3 , 1]]
)

# 味に関する、お寿司と牛丼の比較行列
# 要素1がお寿司
# 要素2が牛丼
taste_mat_1 = Matrix(    
    [[1   , 5,],
     [1/5 , 1]]
)

# 価格に関する、お寿司と牛丼の比較行列
# 要素1がお寿司
# 要素2が牛丼
price_mat_1 = Matrix(    
    [[1 , 1/9,],
     [9 ,   1]]
)

 
基準の重みベクトルを計算します。

# 基準の重みベクトル
eval_weight_1 = calc_ahp_weight_vec(eval_mat_1)
eval_weight_1

$$ \left[\begin{matrix}0.75\\0.25\end{matrix}\right] $$

 
続いて、味に関する、お寿司と牛丼の重みベクトルを計算します。
細かいですが「N」という関数を使うことで、任意の桁数で出力できます。見にくいので、有効数字2桁で丸めました。

# 味に関する、お寿司と牛丼の重みベクトル
taste_weight_1 = calc_ahp_weight_vec(taste_mat_1)
N(taste_weight_1, 2)

$$ \left[\begin{matrix}0.83\\0.17\end{matrix}\right] $$

 
最後に、価格に関する、お寿司と牛丼の重みベクトルを計算します。

# 価格に関する、お寿司と牛丼の重みベクトル
price_weight_1 = calc_ahp_weight_vec(price_mat_1)
price_weight_1

$$ \left[\begin{matrix}0.1\\0.9\end{matrix}\right] $$

 
あとは、「味に関する、お寿司と牛丼の重みベクトル」と「価格に関する、お寿司と牛丼の重みベクトル」に対して、味と価格の重み付きの合計値をとれば総合評価ができますね。
愚直に計算してもよいのですが、せっかくベクトル形式になっているので、行列の掛け算の公式を使って、一発で総合評価を行いたいと思います。

まずはお寿司と牛丼の結果を結合します。

# お寿司と牛丼の結果を結合
join_mat_1 = taste_weight_1.row_join(price_weight_1)
N(join_mat_1, 2)

結果はこちら。
1行目がお寿司で2行目が牛丼です。
1列目が味で、2列目が価格です。

$$ \left[\begin{matrix}0.83 & 0.1\\0.17 & 0.9\end{matrix}\right] $$

 
先のjoin_mat_1に、基準の重みを掛け合わせてやれば、総合評価ができますね。

# 総合評価
# 要素1がお寿司
# 要素2が牛丼
join_mat_1 * eval_weight_1

$$ \left[\begin{matrix}0.65\\0.35\end{matrix}\right] $$

1行目がお寿司なので、やはりお寿司を食べに行くべきだ、という結果になりました。

 

4．3つ以上の比較と比較行列の一貫性

これから、3つ以上の要素があるときのAHPに移ります。
例えば「味・価格・待ち時間」の3つの基準がある中で、食べに行くところを判断する、などが想定されます。
最大固有値をとるときの固有ベクトルを求めるということは同じなのですが、3要素以上になると比較行列の一貫性が満たされているかどうかのチェックが必要になります。
この点をまずは説明します。

 

比較行列の一貫性

比較行列が逆数規則と推移性規則を満たすときに、一貫性を持つといいます。
順にみていきます。

 

逆数規則

たとえば「味は価格よりもやや重要である」と判断されたとき、味は「３」という数値で表現されました。
一方で価格は「1/3」とその逆数とみなされます。それで、以下のような比較行列が得られることになります。

$$ \left[\begin{matrix}1 & 3\\ 1/3 & 1\end{matrix}\right] $$

このように、「A・Bの評価が3なら、B・Aの評価は（逆数の）1/3」になるというのが逆数規則です。
これは比較行列を作る際のルールのようなものですね。ルール通りに比較行列を作成したならば、この条件は満たされているはずです。

 

推移性規則

推移性規則は、比較対象の要素数が3以上になると、考慮しなければいけなくなるものです。

例えば「味が価格よりも3倍重要」であり、かつ「価格は待ち時間よりも5倍重要」であるならば「味は待ち時間よりも3×5=15倍重要」となるとき、推移性を持つといいます。
逆に「味が価格よりも3倍重要」であり、かつ「価格は待ち時間よりも5倍重要」なのに「味は待ち時間と同じくらい重要」というのでは、推移性を持ちません。

「味は価格より大事、価格は時間より大事。それならば、味は時間よりずっと大事に違いない」というのが推移性規則のココロです。
比較対象の要素数が2つだと、気にする必要がないんですが、3つ以上に増えると、要素同士の関係性を気にしないといけないんですね。

 

推移性規則が満たされている例

Pythonによる実装を通して確認します。
まずは推移性を満たしている例から確認します。
比較行列を用意します。

# 基準の行列
# 要素1が味
# 要素2が価格
# 要素3が待ち時間
eval_mat_2 = Matrix(    
    [[1   , 3  , 15],
     [1/3 , 1  , 5],
     [1/15, 1/5, 1]]
)

例えば「味が価格よりも3倍重要」であり、かつ「価格は待ち時間よりも5倍重要」そして、「味は待ち時間よりも3×5=15倍重要」が満たされているので、推移性を満たしていそうです。

固有値、固有ベクトルの計算も問題ありません。

# 最大固有値とその時の多重度・固有ベクトルを取得
eigen_val_vects_2 = eval_mat_2.eigenvects()
max(eigen_val_vects_2, key=(lambda x: x[EIGEN_VAL_IDX]))

$$ \left ( 3.0, \quad 1, \quad \left [ \left[\begin{matrix}15.0\\5.0\\1.0\end{matrix}\right]\right ]\right ) $$

重みベクトルの計算も簡単に終わります。

# 基準の重みベクトル
eval_weight_2 = calc_ahp_weight_vec(eval_mat_2)
N(eval_weight_2, 2)

$$ \left[\begin{matrix}0.71\\0.24\\0.048\end{matrix}\right] $$

 

推移性規則が満たされていない例

続いて、推移性規則が満たされていない例を挙げます。

# 基準の行列
# 要素1が味
# 要素2が価格
# 要素3が待ち時間
eval_mat_3 = Matrix(    
    [[1   , 3  , 1],
     [1/3 , 1  , 5],
     [1   , 1/5, 1]]
)

 
この比較行列eval_mat_3の固有値、固有ベクトルを求めると、なかなか複雑な形になっています（長すぎて画面に収まらないかもしれません）。

eigen_val_vects_3 = eval_mat_3.eigenvects()
eigen_val_vects_3

$$ \left [ \left ( -0.435846103684348 – 1.78464621154911 i, \quad 1, \quad \left [ \left[\begin{matrix}-1.23310603716524 – 2.1358023074901 i\\-1.01370033259557 + 1.75578047970499 i\\1.0\end{matrix}\right]\right ]\right ), \quad \left ( -0.435846103684348 + 1.78464621154911 i, \quad 1, \quad \left [ \left[\begin{matrix}-1.23310603716524 + 2.1358023074901 i\\-1.01370033259557 – 1.75578047970499 i\\1.0\end{matrix}\right]\right ]\right ), \quad \left ( 3.8716922073687, \quad 1, \quad \left [ \left[\begin{matrix}2.46621207433047\\2.02740066519113\\1.0\end{matrix}\right]\right ]\right )\right ] $$

 
目がチカチカしそうですね。これのややこしいところは、虚数が入ってきていることです。
虚数はその大小を判断することが困難なので、以下のようにas_real_imag()を適用して、固有値を虚数部と実数部に分けます。

# 固有値を実数部と虚数部に分ける
eigen_val_vects_3[0][EIGEN_VAL_IDX].as_real_imag()

$$ \left ( -0.435846103684348, \quad -1.78464621154911\right ) $$

実数部だけを取得するコードは以下の通りです。

# 実数部のみ取得
eigen_val_vects_3[0][EIGEN_VAL_IDX].as_real_imag()[0]

$$ -0.435846103684348 $$

上記の結果を応用すると、最大固有値を持つ固有ベクトルを取り出すコードは以下のようになります。

# 実数部のみを取得して、最大固有値とその時の多重度、固有ベクトルを取得
max(eigen_val_vects_3, key=(lambda x: x[EIGEN_VAL_IDX].as_real_imag()[0]))

$$ \left ( 3.8716922073687, \quad 1, \quad \left [ \left[\begin{matrix}2.46621207433047\\2.02740066519113\\1.0\end{matrix}\right]\right ]\right ) $$

 

一貫性の評価

比較対象が3つ以上になると、一貫性(特に推移性)の評価が重要となります。

一貫性を持つ場合は、最大固有値が比較対象数と一致します。「味・価格・待ち時間」の3つがあるならば、最大固有値は3になるはずです。ここからのずれを調べれば良さそうです。
しばしば使われるのが一貫性指標CI(Constency Index)です(西崎(2017))。
CIは以下のように計算されます。ただし\( \lambda_{max} \)は最大固有値で、nは比較対象の数です。

$$ CI = \frac{ \lambda_{max} – n }{ n – 1 } $$

また、ランダムに生成された行列のCIから計算されたランダム指標RIを使う方法もあります。RIはSaaty(2013)で以下のように示されています。

n	3	4	5	6	7	8	9	10
RI	0.52	0.89	1.11	1.25	1.35	1.40	1.45	1.49

上記のRIを使って、一貫性比率CR(Constency Rate)が、以下のように計算されます。

$$ CR = \frac{ CI }{ RI } $$

CIは0.1未満（場合によっては0.15未満）であることが求められます。
CRも同様に0.1未満であることが求められます。

 

Pythonによる一貫性の評価

一貫性指標CIを計算してみます。
まずは、比較対象の数を得ます。これは、比較行列の行数(列数)を使えばよいです。

# 比較行列の、行数と列数を取得
eval_mat_3.shape

$$ \left ( 3, \quad 3\right ) $$

 
一貫性指標CIを計算します。

# 一貫性指標の計算
n = eval_mat_3.shape[0]
max_eigen_val = max(eigen_val_vects_3, key=(lambda x: x[EIGEN_VAL_IDX].as_real_imag()[EIGEN_VAL_IDX]))[EIGEN_VAL_IDX]
ci = (max_eigen_val - n) / (n - 1)
ci

$$ 0.435846103684348 $$

0.1を大きく超えているので、この比較行列は使うべきではないでしょう。
ダメ押しでCRも計算してみます。

# 西崎（2017）『意思決定の数理』を参考に、ランダム指標との比に基づいて評価する

# ランダム指標(初出はSaaty（2013）：
# 『Theory and Applications of the Analytic Network Process: Decision Making With Benefits, Opportunities, Costs, and Risks』)
ri = {3:0.52,
      4:0.89,
      5:1.11,
      6:1.25,
      7:1.35,
      8:1.40,
      9:1.45,
      10:1.49
     }

cr = ci / ri[n]
cr

$$ 0.838165584008362 $$

こちらも0.1を大きく上回ってしまいました。

 

重みベクトルを得る関数の修正

2つの比較において、重みベクトルを計算する関数を作りました。
これを改造して、一貫性指標を出力してくれるようにします。

# 重みベクトルを計算する関数を修正する
# 比較行列から重みベクトルを計算する関数
def calc_ahp_weight_vec_over3(comparison_mat):
    '''
    比較行列から重みベクトルを計算する関数
    一貫性の評価のための指標CIとCRも併せて算出して表示させる
    
    比較対象が3つ以上の時のみ使用できる

    Arguments:

    comparison_mat -- 比較行列
    '''
    
    # 固有値のインデックス
    EIGEN_VAL_IDX = 0
    
    # sympyの関数を使って、固有値と固有ベクトルを得る
    eigen_val_vects = comparison_mat.eigenvects()
    
    # 最大固有値とその時の固有ベクトルを取得
    # 固有値の大小は、実数部で評価
    eigen_val, multiplicity, eigen_vec = max(eigen_val_vects, key=(lambda x: x[EIGEN_VAL_IDX].as_real_imag()))
    
    # 計算過程を出力
    print("================================================================================")

    # ランダム指標(初出はSaaty（2013）：
    # 『Theory and Applications of the Analytic Network Process: Decision Making With Benefits, Opportunities, Costs, and Risks』)
    ri = {3:0.52,
          4:0.89,
          5:1.11,
          6:1.25,
          7:1.35,
          8:1.40,
          9:1.45,
          10:1.49
         }
    
    # 一貫性指標の計算
    n = comparison_mat.shape[0]
    ci = (eigen_val - n) / (n - 1)
    cr = ci / ri[n]

    print("一貫性の評価。CI>0.1（あるいはCI>0.15）ならば、比較行列を修正してください")
    print("比較対象数　　：", n)
    print("最大固有値　　：", N(eigen_val, 2))
    print("一貫性の指標CI：", N(ci, 2))
    print("一貫性の指標CR：", N(cr, 2))
    
    print("================================================================================")
    
    # 重みの合計が1になるように標準化
    weight_vec = eigen_vec[0] / sum(eigen_vec[0])
    
    # 重みを返す
    return(weight_vec)

 
実行すると、以下のように、CIやCRを出力してくれます。これを見て、比較行列を修正するか否かを判断することにします。

# 基準の重みベクトル
eval_weight_3 = calc_ahp_weight_vec_over3(eval_mat_3)
N(eval_weight_3, 2)


================================================================================
一貫性の評価。CI>0.1（あるいはCI>0.15）ならば、比較行列を修正してください
比較対象数　　： 3
最大固有値　　： 3.9
一貫性の指標CI： 0.44
一貫性の指標CR： 0.84
================================================================================


$$ \left[\begin{matrix}0.45\\0.37\\0.18\end{matrix}\right] $$

 

寿司と牛丼、ラーメン問題を解決する

最後に計算例を挙げておきます。

今回扱う事例

目的
休日のランチとして、どのお店に行くかを決める

基準

• 味
• 価格
• 待ち時間

選択肢

• 寿司屋
• 牛丼屋
• ラーメン屋

 

分析コード

まずは、比較行列を指定します。
計算はPythonを使えば一瞬なので、実務上は、この比較行列を得るのが最も大変かもしれませんね。

# 基準の行列
# 要素1が味
# 要素2が価格
# 要素3が時間
eval_mat_4 = Matrix(    
    [[1  , 3,    2],
     [1/3, 1,    1/2],
     [1/2, 2,    1]]
)

# 味に関する、お寿司と牛丼、ラーメンの比較行列
# 要素1がお寿司
# 要素2が牛丼
# 要素3がラーメン
taste_mat_4 = Matrix(    
    [[1  , 3,  2  ],
     [1/3, 1,  1/3],
     [1/2, 3,  1  ]]
)

# 価格に関する、お寿司と牛丼の比較行列
# 要素1がお寿司
# 要素2が牛丼
# 要素3がラーメン
price_mat_4 = Matrix(    
    [[1  , 1/9, 1/5],
     [9  , 1,   3  ],
     [5  , 1/3, 1  ]]
)

# 待ち時間に関する、お寿司と牛丼の比較行列
# 要素1がお寿司
# 要素2が牛丼
# 要素3がラーメン
time_mat_4 = Matrix(    
    [[1  , 1/9, 1/9],
     [9  , 1,   1  ],
     [9  , 1,   1  ]]
)

 
基準の重みベクトルを得ます。

# 基準の重みベクトル
eval_weight_4 = calc_ahp_weight_vec_over3(eval_mat_4)
N(eval_weight_4, 2)


================================================================================
一貫性の評価。CI>0.1（あるいはCI>0.15）ならば、比較行列を修正してください
比較対象数　　： 3
最大固有値　　： 3.0
一貫性の指標CI： 0.0046
一貫性の指標CR： 0.0089
================================================================================


$$ \left[\begin{matrix}0.54\\0.16\\0.3\end{matrix}\right] $$

 
味に関する、お寿司と牛丼、ラーメンの重みベクトルを得ます。

# 味に関する、お寿司と牛丼、ラーメンの重みベクトル
taste_weight_4 = calc_ahp_weight_vec_over3(taste_mat_4)
N(taste_weight_4, 2)


================================================================================
一貫性の評価。CI>0.1（あるいはCI>0.15）ならば、比較行列を修正してください
比較対象数　　： 3
最大固有値　　： 3.1
一貫性の指標CI： 0.027
一貫性の指標CR： 0.052
================================================================================


$$ \left[\begin{matrix}0.53\\0.14\\0.33\end{matrix}\right] $$

 
価格に関する、お寿司と牛丼、ラーメンの重みベクトルを得ます。

# 価格に関する、お寿司と牛丼、ラーメンの重みベクトル
price_weight_4 = calc_ahp_weight_vec_over3(price_mat_4)
N(price_weight_4, 2)


================================================================================
一貫性の評価。CI>0.1（あるいはCI>0.15）ならば、比較行列を修正してください
比較対象数　　： 3
最大固有値　　： 3.0
一貫性の指標CI： 0.015
一貫性の指標CR： 0.028
================================================================================


$$ \left[\begin{matrix}0.063\\0.67\\0.27\end{matrix}\right] $$

 
最後に、待ち時間に関する、お寿司と牛丼、ラーメンの重みベクトルを得ます。

# 時間に関する、お寿司と牛丼、ラーメンの重みベクトル
time_weight_4 = calc_ahp_weight_vec_over3(time_mat_4)
N(time_weight_4, 2)


================================================================================
一貫性の評価。CI>0.1（あるいはCI>0.15）ならば、比較行列を修正してください
比較対象数　　： 3
最大固有値　　： 3.0
一貫性の指標CI： 0
一貫性の指標CR： 0
================================================================================


$$ \left[\begin{matrix}0.053\\0.47\\0.47\end{matrix}\right] $$

 
お寿司・牛丼・ラーメンの結果を結合します。

# 行が選択肢　；お寿司と牛丼、ラーメンの重みベクトル
# 列が基準：味・価格・時間
join_mat_4 = taste_weight_4.row_join(price_weight_4).row_join(time_weight_4)
N(join_mat_4, 2)

$$ \left[\begin{matrix}0.53 & 0.063 & 0.053\\0.14 & 0.67 & 0.47\\0.33 & 0.27 & 0.47\end{matrix}\right] $$

 
いよいよ総合評価です。

# 総合評価
# 要素1がお寿司
# 要素2が牛丼
# 要素3がラーメン
N(join_mat_4 * eval_weight_4, 2)

$$ \left[\begin{matrix}0.31\\0.33\\0.36\end{matrix}\right] $$

僅差ではありますが、ラーメンが最も大きな値となりました。
味はお寿司が最もよかったのですが、価格も待ち時間もともに大きく劣っていたので、お寿司は選ばれなくなりました。

このように、いろいろの判断基準があるときには、AHPを使うことで総合的な評価を下すことが可能となります。

 

AHPには、今回紹介したもの以外にも、いくつかの計算の方法があります。
どのような計算であれ、パソコンを使えば一瞬で計算が終わってしまうわけですが、その内部でどのように評価がなされているのかは、理解しておいた方がよろしいかと思います。

誤り等あれば、メールやコメントなどでご指摘いただけますと大変幸いです。

 

参考文献

西崎(2017)『意思決定の数理 最適な案を選択するための理論と手法   効用分析の基礎からAHPなどの応用的な手法まで記載されている、意思決定の教科書です。

木下(2004)『Q&A:入門意思決定論―戦略的意思決定とは』   オペレーションズ・リサーチ寄りの意思決定論の入門書です。具体例をあげつつ、個別の手法について紹介していくタイプの本です。

Saaty(2013)『Theory and Applications of the Analytic Network Process: Decision Making With Benefits, Opportunities, Costs, and Risks』   AHPやANPに関する説明が詳しく載っています。 西崎(2017)でこの本を引用するときはSaaty(2005)と記載されていましたが、当方はKindle版を読んだので、出版年がずれています。書籍タイトルは同じなので、西崎(2017)で引用されているのと同じ本だと思います。

書籍以外の参考文献

・Sympyの公式ドキュメント

スポンサードリンク

 
更新履歴
2019年3月16日：新規作成