時系列データへの回帰分析
新規作成:2017年05月16日
最終更新:2017年05月16日
ここでは、時系列データを手にした際に、どのような手順で回帰分析をかけていけばいいのか、フローチャートを交えて解説します。
時系列データは特殊でして、普通の回帰分析を行うと、p値がおかしくなり、正しく検定ができなくなることがよくあります。これを見せかけの回帰と呼びます。
シミュレーションを通して、見せかけの回帰という現象を確認したうえで、それらに対応する手法としての単位根検定・共和分検定・一般化最小二乗法(GLS)の基本的な考え方とRでの実装方法について説明します。
ソースコードはまとめてこちらに置いてあります。
スポンサードリンク
目次
- 時系列データへの回帰分析フローチャート
- 単位根と見せかけの回帰
- データチェック1 単位根検定とADF検定
- 解決策1 差分系列への回帰分析
- 差分系列への回帰分析の問題点
- データチェック2 共和分とPO検定
- 自己相関と見せかけの回帰
- データチェック3 ダービンワトソン検定
- 解決策2 一般化最小二乗法(GLS)
1.時系列データへの回帰分析フローチャート
以下に、分析フローチャートを載せます。
なお、誤差分布には正規分布を仮定していることに注意してください。
正規分布以外の確率分布が相手だった場合は、状態空間モデル等で対応することになります。
この記事では状態空間モデルは使わず、比較的容易に実行できると思う計量経済学の手法を使うようにしました。
専門用語が多く出てきますが、各々のキーワードは記事の中で詳細を説明しています。
また、検定の方法はいろいろあり、このフローチャート通りにしてもうまくいかないorこのやり方以外のうまい方法がある場合もあるので、あくまで参考程度にお使いください。
単位根検定
単位根あり ↓ 単位根無し
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
↓ ↓
共和分検定:PO検定 残差の自己相関の検定:ダービンワトソン検定
↓ ↓
共和分あり ↓ 共和分無し 自己相関あり ↓ 自己相関無し
ーーーーーーーーー ーーーーーーーーーーーーーーー
↓ ↓ ↓ ↓
普通の回帰 差分系列へ回帰 一般化最小二乗法(GLS) 普通の回帰
単位根の有無を確認したのち、共和分・残差の自己相関を各々調べます。
そのうえで最適な手法を選ぶという流れになります。
2.単位根と見せかけの回帰
なぜ普通の回帰分析ではダメなのか
回帰分析は「最小二乗法」という手法を用いて推定されます。
例えば「ビールの売り上げ = 気温×傾き +切片」という回帰式を作る際の傾きや切片といったパラメタを推定する手法が最小二乗法となります。
この「普通の最小二乗法」のことをOLS(Ordinary Least Squares)と略することもあります。
この「普通の最小二乗法」はよくできていて、データ分析をする際、よくお世話になるのですが、データが満たさなくてはならない条件がいくつかあります。
その一つがデータの独立性です。
独立でないデータとは、例えば「昨日売り上げが多ければ、今日も売り上げが増える」といったように、「ほかのデータに合わせて自分の値が変わってきてしまう」データなどが挙げられます。このようなデータを「自己相関があるデータ」とも言います。
そして、時系列データでは、この独立性が満たされていることは多くない。
というわけで、「普通の最小二乗法」を使った「普通の回帰分析」では検定が正しくできないことがしばしばあります。
それは例えば「本来ならば無関係の2つのデータに対して、有意な回帰係数が得られてしまう」という問題です。
こういう問題を「見せかけの回帰」と呼びます。
なお、たまに勘違いされるのですが、単位根でなかったとしても、独立性が満たされていなければ、正しく検定することはできません。まずは単位根であるかどうかを判別することが第一ですが、単位根がなかったとしても、自己相関があるかどうかは必ずチェックをします。
単位根とは
単位根をもつデータを「単位根過程」と呼びます。
単位根過程は別名「1次和分過程」とも言われます。
和分とは、文字通り「足し合わせる」という意味ですね。
なので、単位根とは「値が足しあわされて出来上がったデータである」と言えます。
単位根過程の代表として挙げられるのが「ランダムウォーク」です。
ランダムウォークはホワイトノイズの累積和として定義されます。
ホワイトノイズは、自己相関も何もない、正規分布に従った、ただの「ノイズ」です。
このようなノイズの累積和のことを単位根と呼びます。
※単位根の正確な定義は「原系列が非定常過程であり、差分系列が定常過程となる系列のこと」を指しますが、ここでは話の単純化のため、ランダムウォークに絞って解説しています。
単位根過程に対して回帰分析を行うとどうなるか
単位根過程に対して、普通の最小二乗法を適用するとどうなるか、シミュレーションをして確かめてみましょう。
まずは、単位根でない、独立なデータに対して回帰分析を200回実行します。
#--------------------------------------------------------------------------------
# シミュレーションによる回帰係数のp値の確認
# 正しく検定できている場合
#--------------------------------------------------------------------------------
# シミュレーションの回数など
Nsim <- 200
Nsample <- 400
pValues <- numeric(Nsim)
set.seed(1)
for(i in 1:Nsim){
# 自己相関のないシミュレーションデータ
y <- rnorm(Nsample, sd = sqrt(10))
x <- rnorm(Nsample, sd = sqrt(10))
# 線形回帰分析の実行
mod <- lm(y ~ x)
# p値を保存
pValues[i] <- summary(mod)$coefficients[2,4]
}
7,8行目:シミュレーション回数(Nsim)は200回。一回のシミュレーションにおけるサンプルサイズ(Nsample)は400としておきました。
10行目:p値を格納する入れ物を作ります。
12行目:乱数を固定します。乱数は本来、実行するたびに値が変わるのですが、set.seedとすることで、一定の乱数を発生させることができます。
13~23行目:forループを使って、Nsim回(200回)だけ回帰分析を繰り返します。
15,16行目:ただの正規乱数として、x,yの二つのデータを作ります。もちろん両者には何の関係もなく、有意な回帰係数が得られる可能性は低いだろうと予想されます。
19行目:回帰分析を実行して
22行目:p値を保存します。
続いて単位根過程であるランダムウォークにおいて、先ほどと同じようにシミュレーションを行います。
#--------------------------------------------------------------------------------
# シミュレーションによる、見せかけの回帰の確認
# 単位根過程の場合
#--------------------------------------------------------------------------------
pValuesRW <- numeric(Nsim)
set.seed(1)
for(i in 1:Nsim){
# ランダムウォークするシミュレーションデータ
y <- cumsum(rnorm(n=Nsample))
x <- cumsum(rnorm(n=Nsample))
# 線形回帰分析の実行
mod <- lm(y ~ x)
# p値を保存
pValuesRW[i] <- summary(mod)$coefficients[2,4]
}
先ほどと違うのは、『cumsum(rnorm(n=Nsample))』とすることで、乱数の累積和を計算して、それに対して回帰分析を実行している部分です。
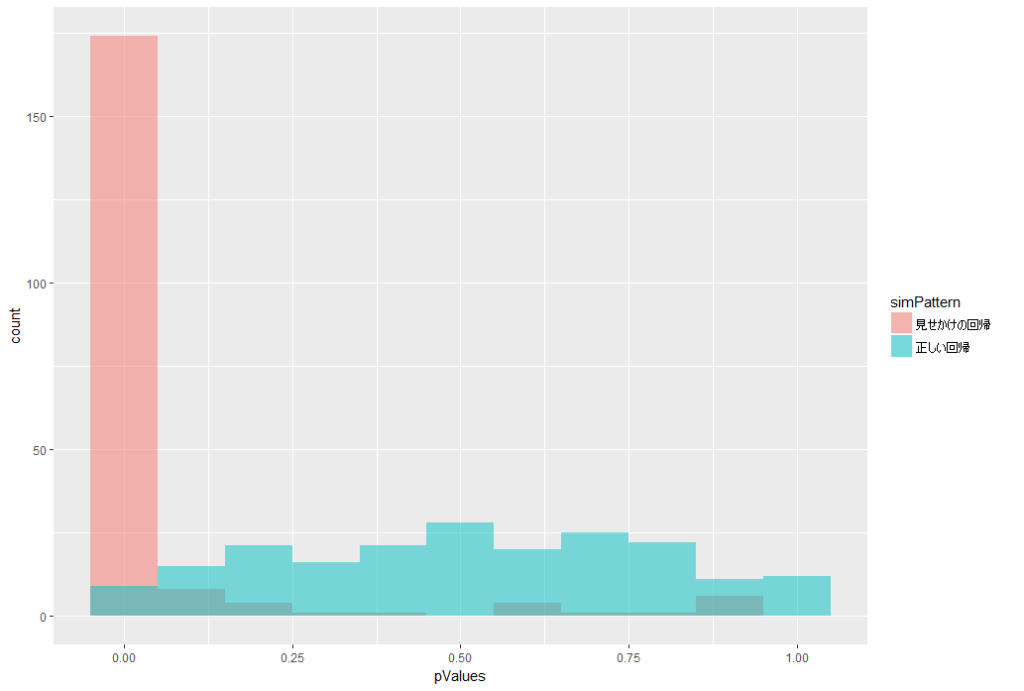
p値のヒストグラムを描きます。
ggplot2というパッケージを使っていることに注意してください。
必要ならば『install.packages(“ggplot2”)』というコマンドを実行して、インストールします。
# データを結合
simResult <- data.frame(
pValues = c(pValues, pValuesRW),
simPattern = rep(c("正しい回帰", "見せかけの回帰"), each = Nsim)
)
# ヒストグラムの描画
library(ggplot2)
histPlot <- ggplot(
simResult,
aes(
x = pValues,
fill = simPattern
)
)
histPlot <- histPlot + geom_histogram(
alpha = 0.5,
position = "identity",
binwidth = 0.1
)
plot(histPlot)
このヒストグラムは、横軸がp値、縦軸が回数となっています。
赤色の、ランダムウォーク系列への回帰分析の結果では、p値が小さな値になっていることがほとんど、すなわち、有意な回帰係数が得られてしまっていることがわかります。
本来ならば無関係な2つの系列に対して、有意な回帰係数が得られてしまう、見せかけの回帰が起こりました。
3.データチェック1 単位根検定とADF検定
単位根系列に対して、普通の回帰分析を行うと良くなさそうでした。
そこで、データが単位根を持っているのか否かをチェックする必要があります。
そこで使われるのが単位根検定です。
単位根検定にはいろいろな種類があるのですが、今回はADF検定を使用します。
ADF検定では、
帰無仮説:単位根がある
対立仮説:単位根がない
として検定します。
なので、p値<0.05であり、帰無仮説が棄却されれば、単位根はないと言えることになります。
「単位根があることの証明」とはならないことに注意してください。
Rでやってみます。
tseriesパッケージの『adf.test』という関数を使います。
またランダムウォークをシミュレーションして作って、y、xという名称で保存しておきます。それらに対してADF検定をかけます。
シミュレーションデータは先ほどのforループの中のコード一部を取り出してきて作りました。
#--------------------------------------------------------------------------------
# 単位根検定
#--------------------------------------------------------------------------------
# ランダムウォークするシミュレーションデータ
set.seed(1)
y <- cumsum(rnorm(n=Nsample))
x <- cumsum(rnorm(n=Nsample))
# install.packages("tseries")
library(tseries)
# 帰無仮説は「単位根過程である」
# 対立仮説は「単位根じゃない」
# 帰無仮説を棄却できないので、「単位根ではないと主張することが難しい」状態。
adf.test(y)
adf.test(x)
結果はこちら
> # 帰無仮説は「単位根過程である」 > # 対立仮説は「単位根じゃない」 > # 帰無仮説を棄却できないので、「単位根ではないと主張することが難しい」状態。 > adf.test(y) Augmented Dickey-Fuller Test data: y Dickey-Fuller = -2.6253, Lag order = 7, p-value = 0.3132 alternative hypothesis: stationary > adf.test(x) Augmented Dickey-Fuller Test data: x Dickey-Fuller = -1.7154, Lag order = 7, p-value = 0.6975 alternative hypothesis: stationary
単位根であることを棄却できませんでした。
このような場合は、データが単位根を持っていることを前提として解析を進めなければなりません。
なお、単位根検定には、ADF検定以外にもPP検定やKPSS検定などもあります。これらを併用して、結果もすべて合わせて記載する論文も見受けられます。
今回はADF検定だけを実行して次に移ります。
4.解決策1 差分系列への回帰分析
単位根を持つデータへ回帰分析をする最も簡単な方法は、差分系列に対して回帰分析を行うことです。
単位根は、和分過程でした。なので、その差分をとってやれば、和分過程ではなくなります。
やってみましょう。
シミュレーションをして、その成果を確認します。
#--------------------------------------------------------------------------------
# 差分系列への回帰分析
#--------------------------------------------------------------------------------
pValuesDiff <- numeric(Nsim)
set.seed(1)
for(i in 1:Nsim){
# ランダムウォークするシミュレーションデータ
y <- cumsum(rnorm(n=Nsample))
x <- cumsum(rnorm(n=Nsample))
# 線形回帰分析の実行
mod <- lm(y ~ x)
# 差分系列をとる
yDiff <- diff(y)
xDiff <- diff(x)
modDiff <- lm(yDiff ~ xDiff)
pValuesDiff[i] <- summary(modDiff)$coefficients[2,4]
}
18,19行目において、データの差分をとっていることに注意してください。
これも200回分のp値を保存してあるので、今までのシミュレーションデータと合わせてp値を比較してみます。
# データを結合
simResult <- data.frame(
pValues = c(pValues, pValuesRW, pValuesDiff),
simPattern = rep(c("正しい回帰", "見せかけの回帰", "差分系列への回帰"), each = Nsim)
)
# ヒストグラムの描画
histPlot <- ggplot(
simResult,
aes(
x = pValues,
fill = simPattern
)
)
histPlot <- histPlot + geom_histogram(
alpha = 0.5,
position = "identity",
binwidth = 0.1
)
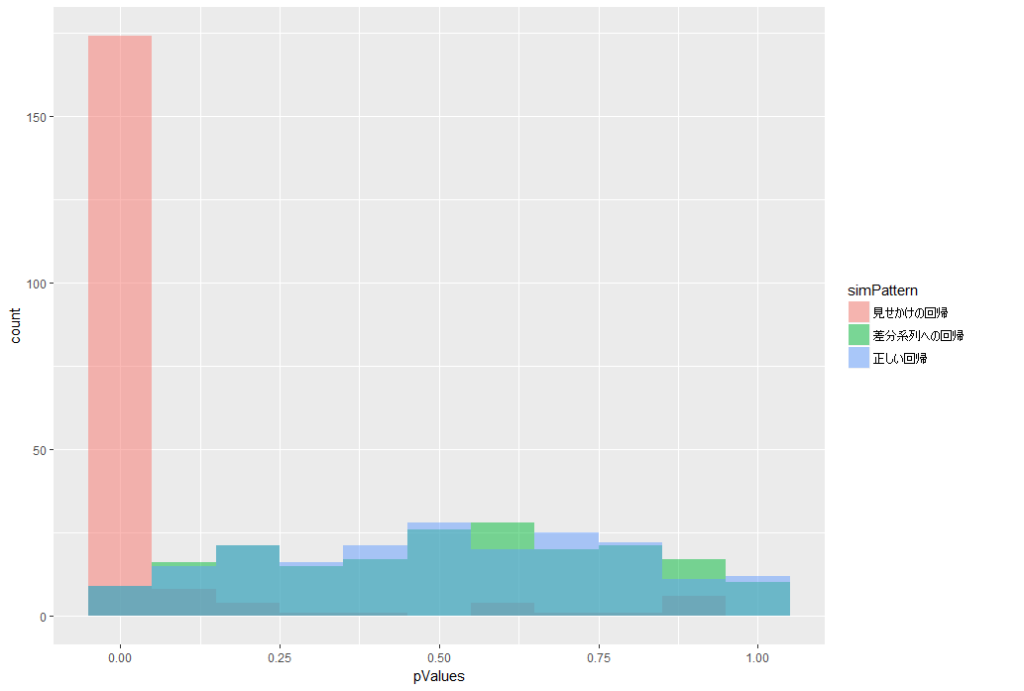
結果はこちら
緑色が、差分系列への回帰分析をした時のp値のヒストグラムです。
青色(正しい回帰)とほぼ同じ結果となっています。
p値が小さくなりすぎる(有意になりやすくなる)ことがなく、正しく検定できました。
5.差分系列への回帰分析の問題点
差分をとってから回帰分析をかける方法には、いくつかの問題点があります。
1つは過剰に差分をとってしまうと、正しく検定ができなくなってしまう問題です。
なので、必ず単位根検定を実施して「単位根がある」と分かった場合のみ、差分をとるようにします。
2つ目の問題は共和分がある時です。
共和分という考え方は次の節で説明しますが、これがある時に差分をとってしまうと、見せかけの回帰とは逆に「本来ならば関係があるのにかかわらず、関係がないと勘違いしてしまう」というミスを犯してしまします。
なので、以下で説明する共和分検定を実施して、共和分がないことを確認してから差分をとるようにします。
※個人的には差分をとるなどのデータの変換はなるべく行いたくないので、状態空間モデルを使用することも検討したほうが良いとは思います。状態空間モデルならば、非定常過程をそのままモデリングできますので。
6.データチェック2 共和分とPO検定
単位根を持つデータ同士に、ある係数をかけてから合計すると、たまに「単位根がなくなる」ことがあります。
そんな関係のことを「共和分」と呼びます。
データが共和分を持っている場合は、たとえ単位根があったとしても、そのまま回帰分析を実行して支障ありません。
共和分を持っているかどうかは、以下の手順で判断します。
1.もともとのデータが単位根を持っていることを確認する
2.単位根があるデータにおいて、回帰分析を実行する
3.回帰分析の結果得られた「残差」が単位根を持っているかどうかを検定する
→単位根がなければ、共和分とみなせる
単純に、実際に回帰分析をしてみて「単位根がなくなる」ことを確認すればよいという理屈です。
なお、この方法をEngle-Grangerの方法と呼びます。
なお、「残差に対する単位根検定」は普通のADF検定ではうまくいきません。
とりあえず「原系列への分析と、一回別の分析を行った後の残差に対する分析とでは、異なる手法を使わなければならないのだ」ということだけ覚えておけばよいかと思います。
そこでADF検定ではなくPO検定を使います。
Engle-Grangerの方法以外にもベクトル誤差修正モデルを用いた方法もあります。
変数が増えた場合は「どの組み合わせが共和分の関係にあるのか」が判別しにくくなります。
そんな時にはベクトル誤差修正モデルを用いて検定を行うのが便利です。
今回はxとyの2つしか変数がない状況を扱うので、Engle-Grangerの方法を採用しました。
やってみましょう。urcaパッケージの『ca.po』という関数を使います。
#--------------------------------------------------------------------------------
# 共和分検定:Engle-Grangerの方法
#--------------------------------------------------------------------------------
# install.packages("urca")
library(urca)
Nsim <- 200
Nsample <- 400
# シミュレーションデータの作成
set.seed(1)
y <- cumsum(rnorm(n=Nsample))
x <- cumsum(rnorm(n=Nsample))
# データをmatrix形式にまとめる
dataM <- matrix(nrow = Nsample, ncol = 2)
dataM[,1] <- y
dataM[,2] <- x
# PO検定の実施
summary(ca.po(dataM, demean = "none"))
ca.po関数には、matrix形式のデータを入れるので、少し整形しておきました。
結果はこちら。
>
> # PO検定の実施
> summary(ca.po(dataM, demean = "none"))
########################################
# Phillips and Ouliaris Unit Root Test #
########################################
Test of type Pu
detrending of series none
Call:
lm(formula = z[, 1] ~ z[, -1] - 1)
Residuals:
Min 1Q Median 3Q Max
-8.767 -1.283 1.796 5.479 13.091
Coefficients:
Estimate Std. Error t value Pr(>|t|)
z[, -1] -0.53200 0.01421 -37.45 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.884 on 399 degrees of freedom
Multiple R-squared: 0.7785, Adjusted R-squared: 0.778
F-statistic: 1403 on 1 and 399 DF, p-value: < 2.2e-16
Value of test-statistic is: 14.861
Critical values of Pu are:
10pct 5pct 1pct
critical values 20.3933 25.9711 38.3413
統計量が「14.861」であり、5パーセント点が「25.9711」です。
帰無仮説:残差が単位根を持つ
対立仮説:残差は単位根を持たない
であるため「残差が単位根を持たないとは言えない」という結果となりました。
普通のランダムウォーク系列同士の回帰分析でしたので、共和分の関係にはなかったということでしょう。
こういうデータであれば、差分をとってから回帰分析をしても、それほど大きな情報の損失にはなりません。
せっかくですので共和分をもつデータもシミュレーションして作ってみましょう。
シミュレーションのコツは「もともとは単位根を持つんだけど、2つの系列を足し合わせると単位根が消える」状況を作ることです。
参考文献にも挙げた沖本先生の本(経済・ファイナンスデータの計量時系列分析)を参考にしてデータを作ります。
#-------------------------------------------------------------------------------- # 参考 # 共和分となっているデータを作って、共和分検定をしてみる #-------------------------------------------------------------------------------- set.seed(1) RW <- cumsum(rnorm(n=Nsample)) x2 <- 0.6 * RW + rnorm(n=Nsample) y2 <- 0.4 * RW + rnorm(n=Nsample)
x2とy2とでおなじ「RW」という変数を使っています。
この「RW」はランダムウォーク系列なので、それを使っているx2,y2もやはり単位根を持ちます。
しかし、x2 – (0.6/0.4)*y2 の計算をしてやると、「RW」が打ち消しあって消えますね。もちろん単位根も消えるはずです。
なので、x2,y2は共和分の関係を持ちます。
まずは、原系列に対して単位根検定(ADF検定)をかけてみます。
> # 両方ともに単位根であることを棄却できない > adf.test(y2) Augmented Dickey-Fuller Test data: y2 Dickey-Fuller = -2.7173, Lag order = 7, p-value = 0.2743 alternative hypothesis: stationary > adf.test(x2) Augmented Dickey-Fuller Test data: x2 Dickey-Fuller = -2.4897, Lag order = 7, p-value = 0.3704 alternative hypothesis: stationary
p値が0.05よりも大きいので「単位根であることを棄却できない」ことになります。
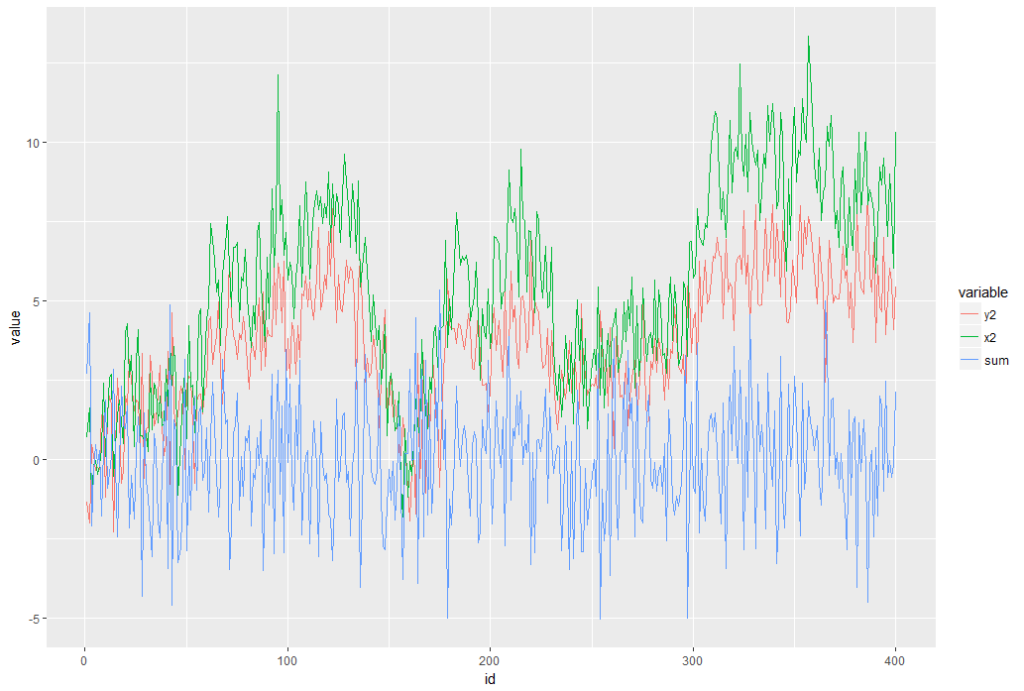
共和分しているデータをグラフに描画してみます。
ggplot2とreshape2パッケージを使っていることに注意してください。
# グラフを見ると、やはりランダムウォークに見える
# ただし特定の係数をかけてから和をとると、ランダムウォークには見えなくなる
df <- data.frame(
id = 1:Nsample,
y2 = y2,
x2 = x2,
sum = x2 - (0.6/0.4)*y2
)
df <- melt(df, id = "id")
linePlot <- ggplot(
df,
aes(
x = id,
y = value,
group = variable,
colour = variable
)
) + geom_line()
plot(linePlot)
結果はこちら。
青い線が「RW」を消したあとの「単位根がなくなった状態」を表しています。
元のx2やy2は上がったり下がったり、ふらふらと移動していきますが、青い線はほぼ一定の値を維持していることに注意してください。
これが共和分の特徴です。
このデータに対して、共和分検定をしてやりましょう。
> # 共和分検定
> dataM2 <- matrix(nrow = Nsample, ncol = 2)
> dataM2[,1] <- y2
> dataM2[,2] <- x2
> summary(ca.po(dataM2, demean = "none"))
########################################
# Phillips and Ouliaris Unit Root Test #
########################################
Test of type Pu
detrending of series none
Call:
lm(formula = z[, 1] ~ z[, -1] - 1)
Residuals:
Min 1Q Median 3Q Max
-3.4650 -0.6586 0.0970 0.9177 3.4208
Coefficients:
Estimate Std. Error t value Pr(>|t|)
z[, -1] 0.64249 0.00997 64.44 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.251 on 399 degrees of freedom
Multiple R-squared: 0.9123, Adjusted R-squared: 0.9121
F-statistic: 4153 on 1 and 399 DF, p-value: < 2.2e-16
Value of test-statistic is: 236.8936
Critical values of Pu are:
10pct 5pct 1pct
critical values 20.3933 25.9711 38.3413
5%点が26くらいなのに関わらず、統計量がおよそ237もありますね。
これで「残差が単位根を持っている」という帰無仮説を棄却することができました。
すなわち、残差には単位根がなく、共和分の関係にあると言えるということです。
この結果に出てきている「Coefficients」は、普通の回帰分析を行った時と変わらない結果ですので、この値を使って考察をしてもかまわないということになります。
なお、うっかりで、共和分を持つデータに対して、差分系列への回帰分析を実行したらどうなってしまうのか、確認してみましょう。
> # 共和分のあるデータに、差分をとってから回帰すると、関係が見えなくなっていしまう
> y2Diff <- diff(y2)
> x2Diff <- diff(x2)
>
> modLmDiffDame <- lm(y2Diff ~ x2Diff)
> summary(modLmDiffDame)
Call:
lm(formula = y2Diff ~ x2Diff)
Residuals:
Min 1Q Median 3Q Max
-4.2689 -0.9975 -0.0603 0.9983 5.4392
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.01614 0.07767 0.208 0.836
x2Diff 0.03659 0.04712 0.777 0.438
Residual standard error: 1.551 on 397 degrees of freedom
Multiple R-squared: 0.001517, Adjusted R-squared: -0.0009984
F-statistic: 0.603 on 1 and 397 DF, p-value: 0.4379
回帰係数は有意とはなりませんでした。
本来ならばx2とy2の間には、何らかの関係があるはずです。それを見過ごしてしまうことになってしまいました。
差分系列への回帰分析は、きわめて簡便で効果の高い手法ではありますが、このような欠点があることも覚えておくとよいかと思います。
スポンサードリンク
7.自己相関と見せかけの回帰
今までの手順で「単位根がある時」の回帰分析ができるようになりました。
次は単位根がないときです。
単位根がないから大丈夫、と安心はできません。
単位根がなかったとしても、自己相関を持つデータであれば、正しく検定ができなくなることが知られています。
※ただし単位根がある時よりかはマシです
少し専門的な話になりますが、OLS推定量の不偏性は担保されます。ただし有効性が担保されないので、やはり検定はしちゃダメです。。
これもシミュレーションをして確認してみましょう。
また、ごくまれに「検定がダメでもAICなら大丈夫なのでは?」と勘違いされる方がいるので、これも確認しておきます。
結論から言うと、AICでもダメです。
#--------------------------------------------------------------------------------
# シミュレーションによる、見せかけの回帰の確認
# 定常過程の場合
#--------------------------------------------------------------------------------
Nsim <- 200
Nsample <- 400
pValuesAutoCol <- numeric(Nsim)
set.seed(1)
AIClm <- numeric(Nsim)
AICnull <- numeric(Nsim)
for(i in 1:Nsim){
# 自己相関のあるシミュレーションデータ
y <- arima.sim(
n = Nsample,sd = sqrt(10),
model = list(order = c(1,0,0), ar = c(0.8))
)
x <- arima.sim(
n = Nsample,sd = sqrt(10),
model = list(order = c(1,0,0), ar = c(0.8))
)
# 線形回帰分析の実行
mod <- lm(y ~ x)
# p値を保存
pValuesAutoCol[i] <- summary(mod)$coefficients[2,4]
# AIC
AIClm[i] <- AIC(mod)
AICnull[i] <- AIC(lm(y ~ 1))
}
『arima.sim』という関数を使うことで、自己相関のあるデータを作成することができます。
p値に加えて「説明変数がある時とないときのAIC」も併せて保存するようにしておきました。
『lm(y ~ 1)』で、説明変数がないときの回帰分析が実行されていることに注意してください。
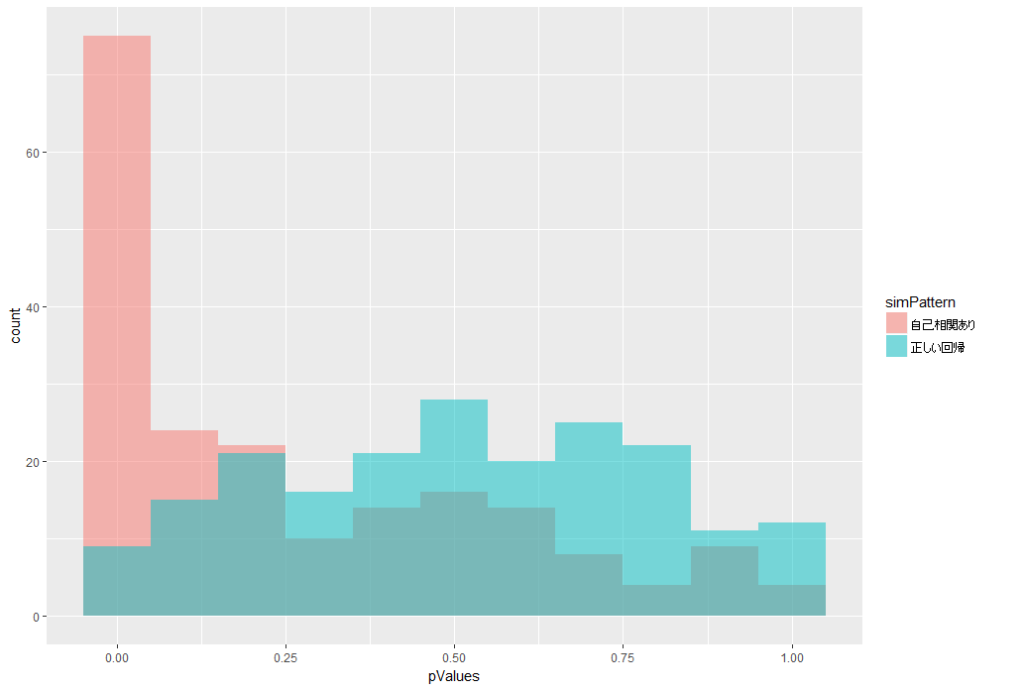
例によってp値のヒストグラムを描いてみます。
ggplot2が使われていることに注意してください。
# データを結合
simResult <- data.frame(
pValues = c(pValues, pValuesAutoCol),
simPattern = rep(c("正しい回帰", "自己相関あり"), each = Nsim)
)
# ヒストグラムの描画
histPlot <- ggplot(
simResult,
aes(
x = pValues,
fill = simPattern
)
)
histPlot <- histPlot + geom_histogram(
alpha = 0.5,
position = "identity",
binwidth = 0.1
)
plot(histPlot)
結果はこちら。
やはりp値が小さくなりやすいことがわかります。
AICも、200回シミュレーションしたうちの半分ほどが誤ったモデルを採用してしまっていることがわかります。
> # AICによるモデル選択もダメ > sum(AIClm < AICnull) / Nsim [1] 0.515
8.データチェック3 ダービンワトソン検定
自己相関が悪い影響を持つことがわかりました。
ということで、自己相関があるかどうかを検定しましょう。
やり方としては、まず普通に回帰分析を行い、その残差を求めます。
その残差に自己相関があるかどうかを検定します。
PO検定の時と同じように、「別の解析を行った結果をさらに検定にかける」ということをするので、少し特別な検定方法を使います。
標準的な方法としてはダービンワトソン検定が挙げられます。
まずはシミュレーションして、データを作ってみます。
先ほどのforループの中の一部を取り出してきました。
#-------------------------------------------------------------------------------- # 残差の自己相関の検定 #-------------------------------------------------------------------------------- set.seed(2) # 自己相関のあるシミュレーションデータ y <- arima.sim( n = Nsample,sd = sqrt(10), model = list(order = c(1,0,0), ar = c(0.8)) ) x <- arima.sim( n = Nsample,sd = sqrt(10), model = list(order = c(1,0,0), ar = c(0.8)) ) autoCorData <- data.frame( y = y, x = x ) # 普通の回帰分析 lmModel <- lm(y ~ x, data = autoCorData)
ダービンワトソン検定はlmtestパッケージの『dwtest』関数を使うことで計算できます。
この関数の引数には、lm関数で推定された回帰モデルを突っ込むことに注意してください。
> # ダービンワトソン検定により、系列相関の有無を検定する
> # 必要なら、パッケージをインストールします
> # install.packages("lmtest")
> library(lmtest)
>
> dwtest(lmModel)
Durbin-Watson test
data: lmModel
DW = 0.3874, p-value < 2.2e-16
alternative hypothesis: true autocorrelation is greater than 0
帰無仮説:残差に自己相関はない
対立仮説:自己相関あり
で、p値がとても小さい(10のマイナス16乗)となったので、自己相関ありとみなすことになります。
9.解決策2 一般化最小二乗法(GLS)
残差に自己相関があることが分かったならば、「普通の最小二乗法(OLS)」は使うことができません。
そこで使われるのが一般化最小二乗法(GLS)です。
GLSだと、残差の自己相関をモデルの中に組み込むことができます。
一般化線形モデル(GLM)と勘違いしやすいので気を付けてください。
MじゃなくてSです。
GLSはnlmeパッケージの、その名も『gls』関数を使うことで計算できます。
残差の自己相関としてはARMAモデルを指定することができます。
ARMAモデルについては時系列解析理論編を参照してください。
とりあえずここでは「様々な残差のパターンを指定することができる」ということだけ覚えていただければOKです。
で、問題はどの残差のパターンにするかです。
それを決めるのにはAICなどのモデル選択の手法を使うのがセオリーです。
やってみます。
#--------------------------------------------------------------------------------
# 一般化最小二乗法の実行
#--------------------------------------------------------------------------------
# install.packages("nlme")
library(nlme)
# 字数を調べる
glsModel_0 <- gls(y ~ x, correlation = NULL , data = autoCorData)
glsModel_1 <- gls(y ~ x, correlation = corARMA(p = 1), data = autoCorData)
glsModel_2 <- gls(y ~ x, correlation = corARMA(p = 2), data = autoCorData)
まずはモデルを組みました。
correlationという引数で、ARMAモデルを指定します。ここを複雑にすると、計算に時間がかかることもあるので気を付けてください。
今回はAR(1)とAR(2)の2つを対象としてみました。
比較のために、自己相関がないモデルも作ってあります。
AICを各々計算して比較します。
> # AR(1)がAIC最小となった
> AIC(
+ glsModel_0,
+ glsModel_1,
+ glsModel_2
+ )
df AIC
glsModel_0 3 2514.397
glsModel_1 4 2090.640
glsModel_2 5 2092.454
AR(1)を残差に組み込んだ「glsModel_1」がAIC最小モデルとなりました。
もちろんAICではなく尤度比検定でもモデル選択は可能です。
これは普通の回帰モデルや一般化線形モデルと同じですね。
> # 尤度比検定もできる。こちらもAR(1)が選ばれた
> anova(glsModel_0, glsModel_1)
Model df AIC BIC logLik Test L.Ratio p-value
glsModel_0 1 3 2514.397 2526.357 -1254.199
glsModel_1 2 4 2090.640 2106.586 -1041.320 1 vs 2 425.7569 <.0001
> anova(glsModel_1, glsModel_2)
Model df AIC BIC logLik Test L.Ratio p-value
glsModel_1 1 4 2090.640 2106.586 -1041.320
glsModel_2 2 5 2092.454 2112.387 -1041.227 1 vs 2 0.1861273 0.6662
> anova(glsModel_0, glsModel_2)
Model df AIC BIC logLik Test L.Ratio p-value
glsModel_0 1 3 2514.397 2526.357 -1254.199
glsModel_2 2 5 2092.454 2112.387 -1041.227 1 vs 2 425.943 <.0001
AIC最小モデルの結果はこちら。
有意な回帰係数は得られないという結果となりました。
> # 推定結果
> summary(glsModel_1)
Generalized least squares fit by REML
Model: y ~ x
Data: autoCorData
AIC BIC logLik
2090.64 2106.586 -1041.32
Correlation Structure: AR(1)
Formula: ~1
Parameter estimate(s):
Phi
0.8165839
Coefficients:
Value Std.Error t-value p-value
(Intercept) 1.4846091 0.8807621 1.6855962 0.0927
x -0.0157816 0.0513654 -0.3072424 0.7588
Correlation:
(Intr)
x -0.054
Standardized residuals:
Min Q1 Med Q3 Max
-2.57816753 -0.77693814 0.01240527 0.65788286 2.68824774
Residual standard error: 5.651155
Degrees of freedom: 400 total; 398 residual
せっかくですので、GLSも200回ほどのシミュレーションにかけてみてp値のヒストグラムを描いてみましょう。
コードを一気に載せます。
これは、計算にやや時間がかかることに注意してください。1、2分くらいです。
#--------------------------------------------------------------------------------
# 一般化最小二乗法のシミュレーション
#--------------------------------------------------------------------------------
pValuesGls <- numeric(Nsim)
set.seed(1)
for(i in 1:Nsim){
# 自己相関のあるシミュレーションデータ
y <- arima.sim(
n = Nsample,
model = list(order = c(1,0,0), ar = c(0.8)),
sd = sqrt(10)
)
x <- arima.sim(
n = Nsample,
model = list(order = c(1,0,0), ar = c(0.8)),
sd = sqrt(10)
)
# 線形回帰分析の実行
mod <- gls(y ~ x, correlation = corARMA(p = 1))
# p値を保存
pValuesGls[i] <- summary(mod)$tTable[2,4]
}
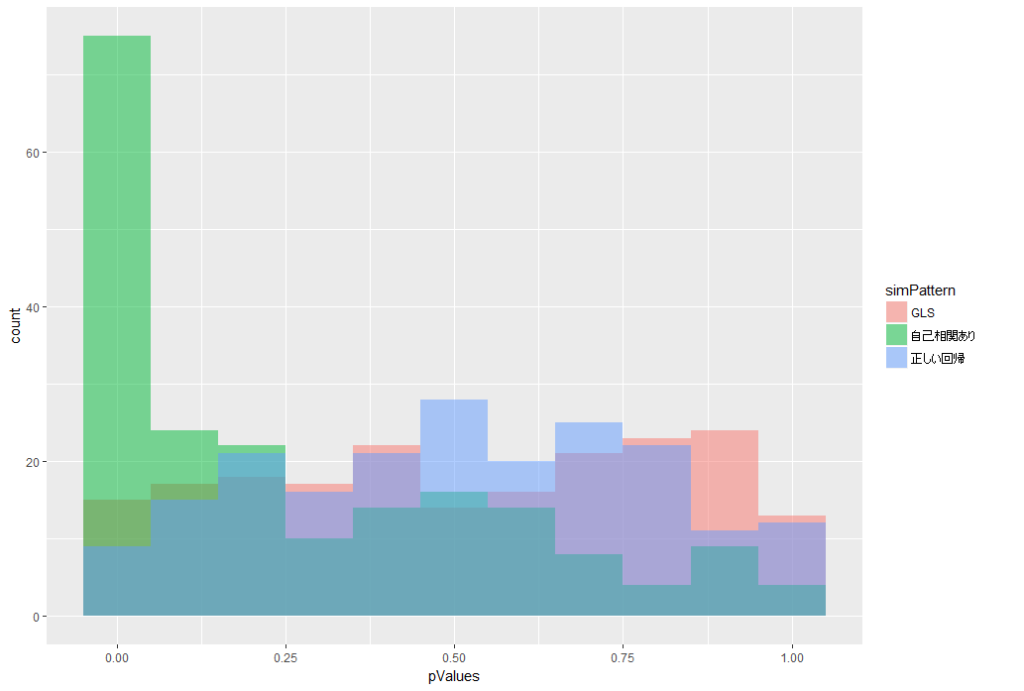
# データを結合
simResult <- data.frame(
pValues = c(pValues, pValuesAutoCol, pValuesGls),
simPattern = rep(c("正しい回帰", "自己相関あり", "GLS"), each = Nsim)
)
# ヒストグラムの描画
histPlot <- ggplot(
simResult,
aes(
x = pValues,
fill = simPattern
)
)
histPlot <- histPlot + geom_histogram(
alpha = 0.5,
position = "identity",
binwidth = 0.1
)
plot(histPlot)
結果はこちら。
赤色がGLSです。p値の偏りがなくなったことがわかります。
今回はシミュレーションデータを使ったので、毎回きれいな結果となりましたが、現実はなかなか泥臭い作業となります。
単位根があることが分かった~差分系列をとった。とした後にもやはり「単位根検定」と「残差の自己相関の検定」は行ったほうが良いかと思います。差分をとったから大丈夫、という訳にはいきません。
今回はデータの特徴がわかっていたのですんなり検定できましたが、単位根検定一つとっても「ドリフトあり」か「定数項あり」か「なにもなし」かで検定のパタンが変わってきます。
実際のデータを扱う際はそこも注意して分析してください。
参考文献
|
Rによる計量経済分析 その名の通り、Rを用いた計量経済分析の手法が一通り載った書籍です。 時系列解析関連の内容も多いです。 今回のRのコードは、多くをこの本を参考にしました。 |
 |
|
経済・ファイナンスデータの計量時系列分析 (統計ライブラリー) このサイトで時系列解析関連の記事を書く際は必ず参照している本です。 時系列解析の基本となる考え方から始めて、モデルの詳しい説明まで載っています。 今、時系列解析を学びたいと思った方はこの本から入ると良いでしょう。 単位根検定や共和分の解説も載っています。 |
 |
書籍以外の参考文献
・六本木で働くデータサイエンティストのブログ|見せかけの回帰について(そして単位根過程・共和分など)
有名なブログ様です。単位根過程における見せかけの回帰についての解説があります。ベクトル誤差修正モデルについても一部言及されているので、興味のある方はぜひ。
スポンサードリンク


はじめてコメントさせて頂きます。初歩的な質問で申し訳ないですが、そもそもデータ同士が共和分関係になる理由は何なのでしょうか?背景にある現象としてはどのようなものがありますか?よく株式のペアトレードでも、共和分が使用されますけど、何故そのペアが共和分になるか背景メカニズムがわかりません。
コメントありがとうございます。
返信が遅れてすいません。
共和分が起こるメカニズムは様々あり、一概には言えません。
2つ以上のデータがいわゆる均衡の関係にあるだろうと想定できる理由があれば、それが共和分を生じさせることがあります。
沖本(2010)「計量時系列分析」では、購買力平価仮説が紹介されていますね。
これは
1.商品Aに対して、
安い国で買って、高い国で売れば、濡れ手で粟で儲かる
2.そんなうまい儲け話は、長く続かないはずだ
3.為替レートを調整すれば、国ごとに価格の違いは生まれないはずだ
→というわけで、為替レートと物価水準は(長期的に見たら)均衡関係にある
この仮定が満たされる場合には、購買力平価仮説が、
為替レートと物価水準の間で共和分を生じさせるメカニズムになります。
ペアトレードの場合は、メカニズムには着目せずに
「共和分があれば、均衡関係がある」という信念だけに着目しているのでしょう。