2017年5月30日 / 最終更新日時 : 2017年9月9日馬場真哉 Pythonデータ分析

Pythonによる状態空間モデル

最終更新：2017年06月06日

Pythonを用いた、状態空間モデルの実装方法について説明します。
なお、正規線形状態空間モデル（動的線形モデル）のみをここでは扱います。

Pythonを使えば、カルマンフィルタや最尤法によるパラメタ推定を短いコードで簡潔に実装することができます。

なお、この記事ではOSはWindows。Pythonは『Python 3.6.0 :: Anaconda custom (64-bit)』を使用して、JupyterNotebook上で計算を実行しました。
JupyterNotebookの出力はリンク先を参照してください。

スポンサードリンク

1．状態空間モデルとPython時系列分析

今までのARIMAモデルを主とした時系列モデルは、予測しかできませんでした。
しかし、状態空間モデルを使えば、予測だけでなく、「データの解釈」を進めることができます。

毎日の売り上げデータや、時間ごとの電力需要量データといった「時系列データ」を分析するモチベーションとしては、まずは「将来を予測したい」というのがあげられるでしょう。
昨日売り上げが多かったら、今日も多いだろう、という予測ができれば、商品を多めに仕入れておくなどの対策をとることができますね。電力需要に関しても同じです。
将来起こることが予測できていれば、あらかじめ対策をとることができます。

しかし、ARIMAモデルなどのBox-Jenkins法は、内部がブラックボックス化しており、データの解釈は困難でした。

そこで出てくるのが状態空間モデルです。
「なぜ状態空間モデルを使うのか」でも説明したように、状態空間モデルは色々なバリエーションを持たせることができる、汎用的な統計モデルです。
データの構造を想像しながら、データによく合うモデルを自由に選ぶことができます。
先に紹介したARIMAモデルも状態空間モデルとして表現し、モデル化することができます。より「一般的な」統計モデルが状態空間モデルなのです。
データによく合うモデルを構築することができれば、予測精度も向上するかもしれませんね。

この記事では、様々な「状態空間モデルの型」をデータに対して適用していきます。
型を変えることによって、結果が柔軟に変わっていく様子をぜひ確認して下さい。

また、赤池の情報量規準(AIC)を使ったモデル選択も行うことができるので「最も良い型」を選ぶこともできます。

もちろん既存のARIMAモデルなどのBox-Jenkins法が悪いわけではありません。
予測だけでよいというのならば、これらも候補に入ってくるでしょう。
Pythonを使ったARIMAモデルの推定に関しては「Pythonによる時系列分析の基礎」を参照してください。

状態空間モデルの詳しい解説はこの記事では行いません。
興味のある方は「状態空間モデル」の記事を参照してください。R言語を使っていますが、考え方は変わりません。

2．データの読み込み

Jupyter NoteBookの計算結果はリンク先に載せてあります。

まずは、ライブラリを一気に読み込みます。

# 基本のライブラリを読み込む
import numpy as np
import pandas as pd
from scipy import stats

# グラフ描画
from matplotlib import pylab as plt
import seaborn as sns
%matplotlib inline

# グラフを横長にする
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 15, 6

# 統計モデル
import statsmodels.api as sm

今回は、月ごとの飛行機の乗客数データを対象とします。期間は1949年1月から1960年12月までです。
初出は「Box, G. E. P., Jenkins, G. M. and Reinsel, G. C. (1976) Time Series Analysis, Forecasting and Control. Third Edition. Holden-Day. Series G.」となります。
以下のURLから、データの詳細を確認できます（R言語の記事です）
https://stat.ethz.ch/R-manual/R-devel/library/datasets/html/AirPassengers.html

R言語では組み込みデータセットとして用意されているのですが、Pythonだと見当たらなかったので、CSVファイルから読み込みます。
以下のサイトにファイルがあったので、それを使いました。

A comprehensive beginner’s guide to create a Time Series Forecast (with Codes in Python)

ダウンロードする対象のファイルのリンクも張っておきます（外部サイトです）
AirPassengers

なお、このデータの1列目は日付です。そのためExcelなどで開いてから保存すると、よくわからない形式に変換されてしまうので気を付けてください。ファイルを開く場合は、メモ帳などのテキストエディタを使うようにしてください。

データを読み込み「ts」という名称で日付形式にして保存します。
何をやっているのか全く分からん、という方は「Pythonによる時系列分析の基礎」も参照してください。

# 日付形式で読み込む
dateparse = lambda dates: pd.datetime.strptime(dates, '%Y-%m')
data = pd.read_csv('AirPassengers.csv', index_col='Month', date_parser=dateparse, dtype='float')

# 日付形式にする
ts = data['#Passengers'] 
ts.head()

# プロット
plt.plot(ts)

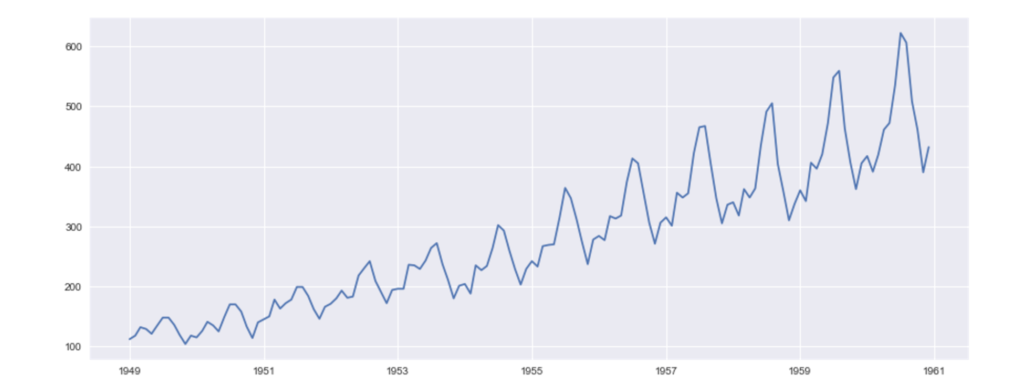
プロットした結果は以下の通りです。
右肩上がりのトレンド、年単位での周期的な変動があることが想像できます。

3．ローカルレベルモデルの推定

Jupyter NoteBookの計算結果はリンク先に載せてあります。

ローカルレベルモデルの詳細は「ローカルレベルモデル」を参照してください。
ここではごく簡単な解説にとどめます。

まず、時系列データがどのように作られているかを考えます。

状態空間モデルでは「状態空間表現」という便利な表現のためのフレームワークが用意されているのでそれを使いましょう。

まずは一番単純な形を考えてみます。

　　　　状態＝前期の状態
　　　　 ↓
観測＝状態

このパターンだと、「ずーっとおなじデータが得られる」ことになります。
例えば1950年1月の飛行機乗客数が100人だったら、2月も3月もずーっと100人。

こんなはずはないだろうと。
そこで「不確実なノイズ」を突っ込みます。

　　　　状態＝前期の状態
　　　　 ↓
観測～状態＋観測誤差

これで「状態がずーっと100人のまま」だったとしても、観測結果が得られるたびにノイズが入ってくるので、乗客数は102人とか95人とかにぶれることになります。

でも、このやり方だと「ずーっと100人の前後をばらつくだけ」ということになります。
データを見た感じだと、そんなことなさそうでしたよね。
やっぱり状態も毎年変わってほしいかなーと思うわけです。

なので、以下のようにします。

　　　　状態～前期の状態　＋システム誤差
　　　　 ↓
観測～状態＋観測誤差

状態も毎回ノイズが入って、脈々と変わっていきます。
1949年の初期のころにはお客さんの数は少なかったんだけど、1960年まで来るとお客さんの数は増えている。そんな状況もある程度これであらわすことができますね。

ただ単にノイズを突っ込んだだけなのですが、その割にはとても高い表現力を持っているのがこの「ローカルレベルモデル」です。

実装してみましょう。
Pythonのstatmodelsライブラリを使えば支障なく計算できます。

ただしこいつのバージョン0.8.0以上でなければ状態空間モデルが推定できません。
以下のコードを実行しようとして「そんな計算はできません」とPythonに怒られた場合は、statmodelsのバージョンを上げてください。

WindowsでAnacondaを使用している場合は、コマンドプロンプトを起動して、以下のコマンドを実行すればOKです。
なお、2017年5月30日時点では0.8.0でよいのですが、この記事をご覧になっている方がもっと未来に読まれていた場合は、適宜最新のバージョンを入れるようにしてください。

conda install -c taugspurger statsmodels=0.8.0

では、ローカルレベルモデルを推定します。
モデルの作成～パラメタ推定～推定されたパラメタの表示～推定された状態の図示まで一気にやってしまいます。

# ローカルレベルモデルの推定
mod_local_level = sm.tsa.UnobservedComponents(ts, 'local level')

# 最尤法によるパラメタの推定
res_local_level = mod_local_level.fit()

# 推定されたパラメタ一覧
print(res_local_level.summary())

# 推定された状態・トレンドの描画
rcParams['figure.figsize'] = 15, 15
fig = res_local_level.plot_components()

まず、状態空間モデルは『UnobservedComponents』という関数を使って推定します。
引数には、対象となるデータと「推定したいモデルの型」を入れておきます。今回はローカルレベルモデルなので「local level」としておきます。

パラメタの推定は「fit」関数を適用するだけです。
今回は引数無しで実行しました。

8行目で『summary』関数を適用して推定されたパラメタ（今回は観測誤差と過程誤差（システムノイズ）の分散）の一覧などを表示させます。

12行目で推定された状態を図示します。

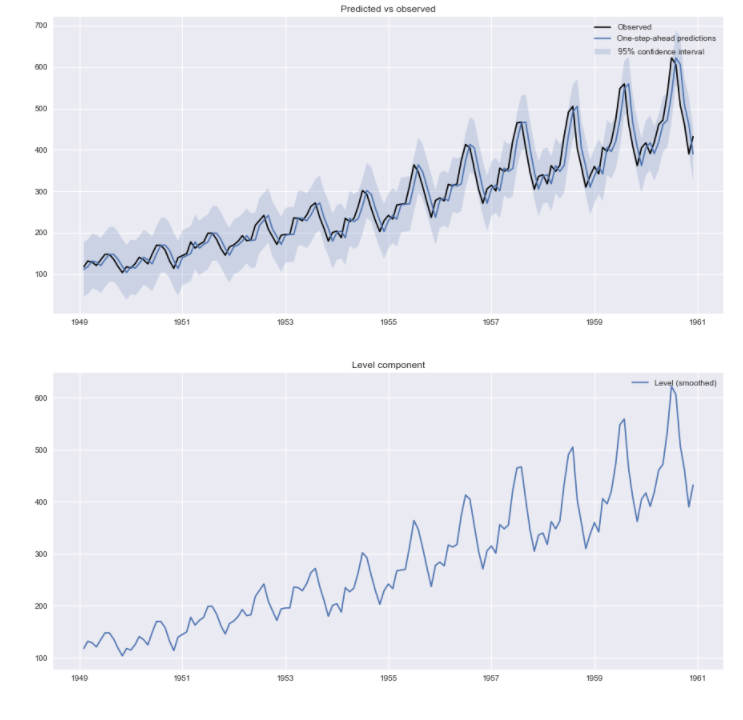
パラメタについてはリンク先を見ていただくとして、推定された状態のグラフを見てみましょう。

一つ目のグラフが、観測値と予測結果の比較のグラフ。2つ目が推定された状態のグラフです。
1つ目を見ると黒い線の観測値と青い線の予測値がちょうど1か月だけずれていることがわかります。
ローカルレベルモデルは推定は簡単なのですが、じつは「来期の予測値は前期の観測値と同じ」という予測結果を出します。なので予測はあまりぱっとしない感じになります。
逆に言えば、ローカルレベルモデル以上の予測結果が出せなければ、複雑なモデルを使う意味がないということですね。

というわけで、少しずつモデルを複雑にしていきましょう。

4．ローカル線形トレンドモデルの推定

なんだか右肩上がりのトレンドがありそうでしたので、「状態は毎年トレンドに従って上下する」と考えてモデルを組みなおしましょう。

　　　　　　　　　　　　　　　　　　トレンド　～　前期のトレンド　＋　システム誤差２
　　　　　　　　　　　　　　　　　　　 ↓
　　　　　状態　～　前期の状態　＋　トレンド　＋　システム誤差１
　　　　　 ↓
観測　～　状態　＋　観測誤差

トレンドが入りました。
なお、このトレンドも毎期にノイズが入って変化します。
1949年はすごく大きな上昇トレンドがあるが、1960年に入ると伸び悩む、なんてことがもしあるならば、これでうまくモデル化ができるはずです。

やってみましょう。
実装は難しくありません。さっき「local level」と指定していた部分を「local linear trend」に変えてやるだけでOKです。

# ローカル線形トレンドモデル

mod_trend = sm.tsa.UnobservedComponents(
    ts,
    'local linear trend'
)

# 最尤法によるパラメタの推定
# ワーニングが出たのでBFGS法で最適化する
res_trend = mod_trend.fit(method='bfgs')

# 推定されたパラメタ一覧
print(res_trend.summary())

# 推定された状態・トレンドの描画
rcParams['figure.figsize'] = 15, 20
fig = res_trend.plot_components()

なお、最尤法の実行の際、ワーニングが出たので、最適化の手法をBFGSに変えてあります（もともとはL-BFGS）。

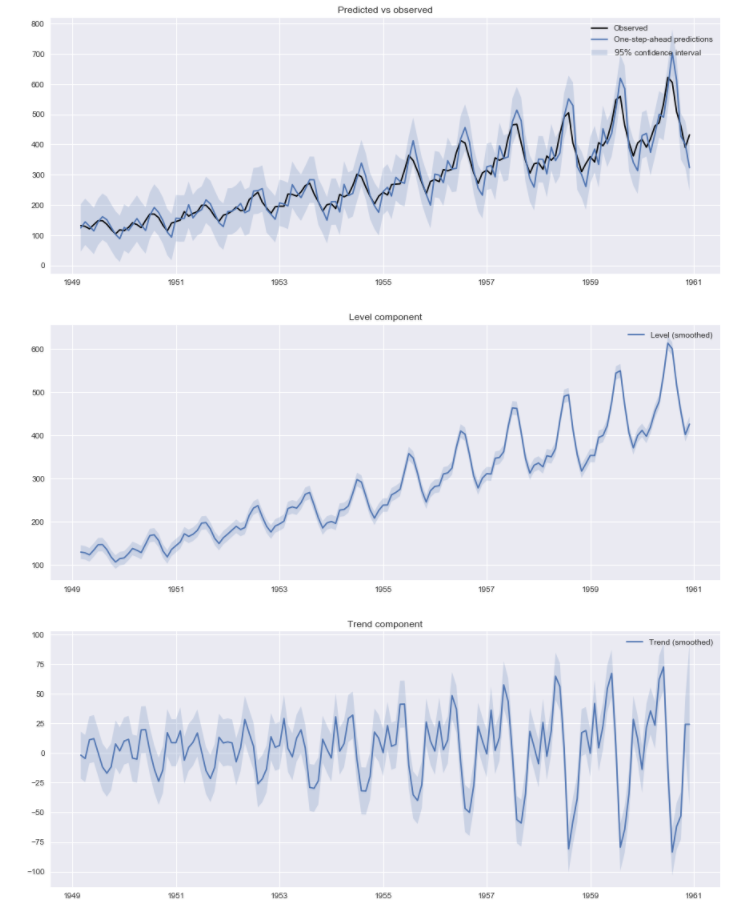
こちらも推定結果のグラフだけ載せておきます。

3つ目のグラフがトレンドを表しているのですが、相当にグネグネと変わってきています。
これは季節の周期的な変動をトレンドで無理やり表そうとしたのが原因でしょう。
というわけで、次は季節をモデルに組み込みます。

スポンサードリンク

5．季節変動の取り込み

季節の効果をモデルに組み込みましょう。
Pythonでは引数に「seasonal=12」と指定するだけで12か月単位の周期を表すことができます。
せっかくですので、ローカルレベルモデルとローカル線形トレンドモデルの両方で季節変動を組み込んでみます。

# 季節変動ありのローカルレベルモデル

mod_season_local_level = sm.tsa.UnobservedComponents(
    ts,
    'local level',
    seasonal=12
)

# まずはNelder-Meadでパラメタを推定し、その結果を初期値としてまた最適化する。2回目はBFGSを使用。
res_season_local_level = mod_season_local_level.fit(
    method='bfgs', 
    maxiter=500, 
    start_params=mod_season_local_level.fit(method='nm', maxiter=500).params,
)

# 推定されたパラメタ一覧
print(res_season_local_level.summary())

# 推定された状態・トレンド・季節の影響の描画
rcParams['figure.figsize'] = 15, 20
fig = res_season_local_level.plot_components()

6行目に「seasonal=12」を指定して、季節成分を入れています。
また、ここからは、パラメタ推定がなかなかうまくいかないことが増えてきますので、最適化を2回実行するようにしました。

ちょっと工夫したパラメタの推定の方法について説明します。10行目以降に注目してください。
パラメタ推定の際「パラメタの初期値」を指定してやることができます。
その初期値に「method=’nm’」で指定されたNelder-Mead法で推定されたパラメタを使います。
Nelder-Meadで推定されたパラメタを初期値としてつかって、さらにBFGS法でパラメタを推定しました。
これくらいやらないとうまくパラメタが推定できません。

fit関数についてはこちらの資料でその詳細を確認することができます。
一度は読んでおいた方がよろしいかと思います。
methodとmaxiter（最大繰り返し数）は頻繁に弄ることになりますので。

なお、2段階に分けてパラメタを推定したからといってうまくいく保証はありません。
どうもR言語のdlmパッケージで推定されたパラメタとはちょっと違う結果になっているようです。
ここでは細かいパラメタの推定値の評価は行わず、モデルの実装方法のみを解説します。
実際のデータ分析に応用する際には、図示やパラメタの評価を通して「まとも」あるいは「直観に合致する」モデルになっているかどうかを必ず確認するようにしてください。

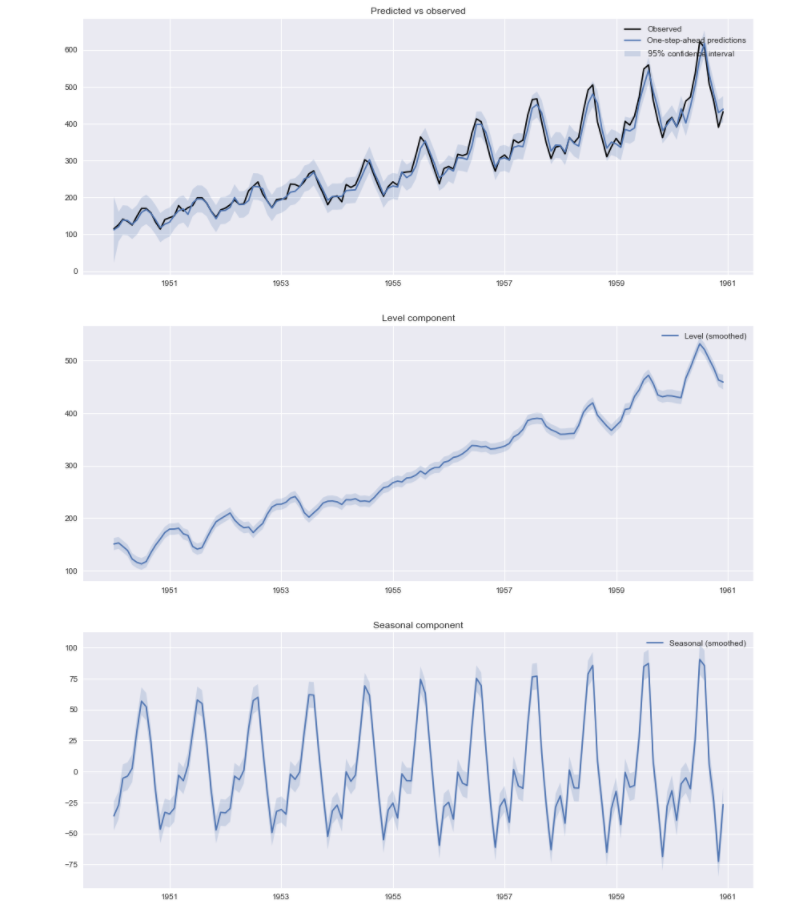
季節成分有りのローカルレベルモデルの推定結果はこちら。

一番下が季節成分です。

次は、季節成分有りのローカル線形トレンドモデルを推定してみましょう。

# 季節変動ありのローカル線形トレンドモデル

mod_season_trend = sm.tsa.UnobservedComponents(
    ts,
    'local linear trend',
    seasonal=12
)

# まずはNelder-Meadでパラメタを推定し、その結果を初期値としてまた最適化する。2回目はBFGSを使用。
res_season_trend = mod_season_trend.fit(
    method='bfgs', 
    maxiter=500, 
    start_params=mod_season_trend.fit(method='nm', maxiter=500).params,
)

# 推定されたパラメタ一覧
print(res_season_trend.summary())

# 推定された状態・トレンド・季節の影響の描画
rcParams['figure.figsize'] = 15, 20
fig = res_season_trend.plot_components()

結果はこちら。
トレンドがほぼ一定の値となったことに注目してください。

6．推定するパラメタの数を減らす

先ほどの「季節成分有りのローカル線形トレンドモデル」のパラメタの推定結果を見てみます。

sigma2.irregular　　5.508e-12 sigma2.level　　　　161.5594 sigma2.trend　　　　1.934e-11 sigma2.seasonal　　 18.8401

上から順番に
観測誤差の分散（sigma2.irregular）
状態のシステムノイズ（sigma2.level）
トレンドのシステムノイズ（sigma2.trend）
季節成分のシステムノイズ（sigma2.seasonal）
です。

観測誤差の分散（sigma2.irregular）とトレンドのシステムノイズ（sigma2.trend）がとても小さくなっていることがわかります。
トレンドは毎月一定である（毎月同じペースで乗客数が増えている）のかもしれませんね。
また、乗客数は飛行場で厳密に記録されているため、観測誤差を0とみなすこともできるのかもしれません。
観測誤差がないということは野外の調査では考えにくいのですが、飛行機の乗客数なら、集計ミスがない限りはこのように考えることもできなくはありません。

というわけで、各々のノイズを取り除いてみましょう。

まずは見るからになさそうだった、トレンドのシステムノイズを除外します。
このとき『UnobservedComponents』の引数に「local linear deterministic trend」を指定します。こうすることで、ローカル線形トレンドモデルからトレンドのシステムノイズだけをなくすことができます。
こういった引数に何を入れるかについては『UnobservedComponents』のマニュアルに細かく載っていますので合わせて参照してください。

コードだけ載せます。

# 詳細は以下の資料を参照してください
# http://www.statsmodels.org/stable/generated/statsmodels.tsa.statespace.structural.UnobservedComponents.html#statsmodels.tsa.statespace.structural.UnobservedComponents

# 季節変動ありのローカル線形トレンドモデル
# ただし、トレンドの分散は無し

mod_season_trend_d = sm.tsa.UnobservedComponents(
    ts,
    'local linear deterministic trend',
    seasonal=12
)

# まずはNelder-Meadでパラメタを推定し、その結果を初期値としてまた最適化する。2回目はBFGSを使用。
res_season_trend_d = mod_season_trend_d.fit(
    method='bfgs', 
    maxiter=500, 
    start_params=mod_season_trend_d.fit(method='nm', maxiter=500).params,
)

# 推定されたパラメタ一覧
print(res_season_trend_d.summary())

# 推定された状態・トレンド・季節の影響の描画
rcParams['figure.figsize'] = 15, 20
fig = res_season_trend_d.plot_components()

次は観測誤差の分散も、推定するのをやめにします。
モデルの型に「random walk with drift」を指定します。

# 詳細は以下の資料を参照してください
# http://www.statsmodels.org/stable/generated/statsmodels.tsa.statespace.structural.UnobservedComponents.html#statsmodels.tsa.statespace.structural.UnobservedComponents

# 季節変動ありのローカル線形トレンドモデル
# ただし、トレンドと観測誤差の分散は無し

mod_season_rw = sm.tsa.UnobservedComponents(
    ts,
    'random walk with drift',
    seasonal=12
)

# まずはNelder-Meadでパラメタを推定し、その結果を初期値としてまた最適化する。2回目はBFGSを使用。
res_season_rw = mod_season_rw.fit(
    method='bfgs', 
    maxiter=500, 
    start_params=mod_season_rw.fit(method='nm', maxiter=500).params,
)

# 推定されたパラメタ一覧
print(res_season_rw.summary())

# 推定された状態・トレンド・季節の影響の描画
rcParams['figure.figsize'] = 15, 20
fig = res_season_rw.plot_components()

7．モデルの比較と将来予測

今まで、かなりたくさんのパターンのモデルを作って来ました。
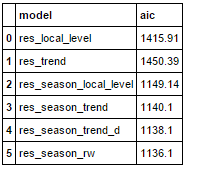
この中で最もAICが低いモデルを選びます。

# 今まで計算してきたモデルのAICを格納する
aic_list = pd.DataFrame(index=range(6), columns=["model", "aic"])

aic_list.ix[0]["model"] = "res_local_level"
aic_list.ix[0]["aic"] = res_local_level.aic

aic_list.ix[1]["model"] = "res_trend"
aic_list.ix[1]["aic"] = res_trend.aic

aic_list.ix[2]["model"] = "res_season_local_level"
aic_list.ix[2]["aic"] = res_season_local_level.aic

aic_list.ix[3]["model"] = "res_season_trend"
aic_list.ix[3]["aic"] = res_season_trend.aic

aic_list.ix[4]["model"] = "res_season_trend_d"
aic_list.ix[4]["aic"] = res_season_trend_d.aic

aic_list.ix[5]["model"] = "res_season_rw"
aic_list.ix[5]["aic"] = res_season_rw.aic

# 結果の表示
aic_list

結果はこちら。
どうやら、最後に組んだ「トレンドのシステムノイズと観測誤差がない、季節付きローカル線形トレンドモデル」が最も良いことになりました。
このモデルはマニュアルでは「ドリフト付きランダムウォークモデル」と呼ばれているようです。

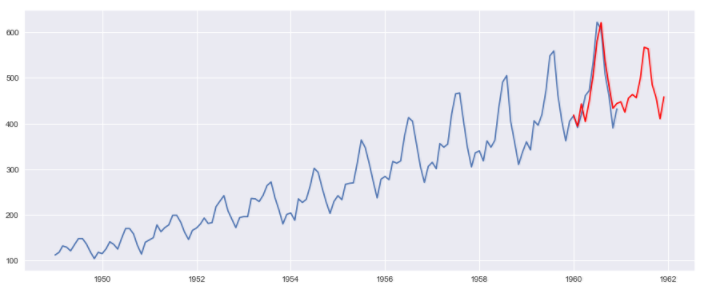
それでは、AIC最小モデルを使って予測をしてみましょう。

# 予測
pred = res_season_rw.predict('1960-01-01', '1961-12-01')

# 実データと予測結果の図示
rcParams['figure.figsize'] = 15, 6
plt.plot(ts)
plt.plot(pred, "r")

実装の方法だけで見ると、かなり洗練されており、R言語のdlmパッケージを使った場合よりも短いコードでモデル化～図示、予測が可能です。

WebでPythonを学ぶなら

実践 Python データサイエンス

動画でPythonやJupyter Notebookの使い方を学ぶことができる勉強サイトです。
Udemyを利用すると、Pythonやデータ分析を「基礎から順にステップアップする内容で、かつ動画で」学ぶことができます。
ネットで受ける通信教育、みたいな感じです。
管理人も受講してみました。体験記はこちらから読めます。

参考文献

予測にいかす統計モデリングの基本

この記事で扱っているカルマンフィルタではなく粒子フィルタが主ではありますが、図を使って状態空間モデルを解説しているので、状態空間モデルの構造がわかりやすくなっています。
予測～フィルタリング～スムージングの流れに関しても図で解説があります。

カルマンフィルタ ―Rを使った時系列予測と状態空間モデル―

薄い本ですが、内容は濃いです。数式だけでなくR言語を使った解説があるのがポイント。
この手の薄い本はえげつないくらい数式が多いのがたまにあるのですが、これはそこまでではありません。日本語での解説も丁寧ですのでお勧め。これも良書だと思います。

状態空間時系列分析入門

このサイトでもよく紹介している状態空間モデルの入門書です。
状態空間モデルというモデルの考え方を解説した、初学者向けの良書です。

Think Stats 第2版 ―プログラマのための統計入門

Pythonでデータ分析をするための入門書です。統計学の理論に関する説明は少なめですが、とりあえずコードを書いて勉強したいという場合に良いかと思います。
状態空間モデルの解説はないものの、時系列分析も1章載っています。

書籍以外の参考文献

statsmodels.tsa.statespace.structural.UnobservedComponents
状態空間モデルを推定する関数のマニュアルです。

スポンサードリンク