カルマンフィルタの考え方
カルマンフィルタは、状態空間モデルにおいて、内部の見えない「状態」を効率的に推定するための計算手法です。
カルマンフィルタを理解するためには、まず状態空間モデルが何なのかを理解することが必要です。そのうえでカルマンフィルタの考え方と計算方法を学びます。
この記事では、状態空間モデルもカルマンフィルタもあまり詳しくないという方を対象として、カルマンフィルタの考え方とライブラリを使わない実装方法について説明します。
最後に、R言語における有名なカルマンフィルタの計算パッケージである「dlmパッケージ」の簡単な使い方も解説します。
ソースコードはまとめてこちらに載せてあります。
ブログの内容が本になりました。
書籍サポートページはこちらです
スポンサードリンク
目次
- 状態空間モデルの概要
- 状態空間モデルとカルマンフィルタの関係
- カルマンフィルタの考え方
- ライブラリを使わないカルマンフィルタの実装
- パラメタを変えたときの挙動
- dlmパッケージを使ったカルマンフィルタ
1.状態空間モデルの概要
状態空間モデルとは
状態空間モデルは、その名の通り「状態」を推定します。
例えば、ある湖で魚釣りをしたとしましょう。5尾釣れました。翌日は7尾つれました。
釣れた尾数は「観測値」と呼ばれます。
ところで、2日目のほうが魚が多く釣れたようですが、これは、湖の中にいる魚の数が増えたとみなすことができるでしょうか。
釣れた尾数であるところの「観測値」対比として、湖にいる魚の数を「状態」と呼びます。
私たちが得ることができるのは「観測値」だけです。
けれども、湖の中にどれくらい魚がいるのかを推定できれば、魚の数を維持・管理しやすくなりますね。だから「状態」を知りたい。
そういったニーズに対応してくれるのが状態空間モデルです。
状態空間モデルは、大きく2つの領域で使われます。
1つは制御。
センサーなどから得られる情報を「観測値」として、そこから「状態」を推定します。推定された「状態」に基づいて制御を行います。例えばアポロ計画では、センサーの情報から、宇宙船の正しい位置を推定し、進行方向の調整などを行いました。
モノづくりなどにも応用されていますね。
2つ目はデータ分析です。
釣獲尾数から魚の資源量を推定したり、売り上げという「観測値」から潜在顧客数という「状態」を推定することもできるでしょう。
観測方程式と状態方程式
状態空間モデルといっても、様々なバリエーションがあります。
例えば、魚の数を推定するモデルと、宇宙船の場所を調べるモデルがまったく同じということは考えにくいですね。
「観測値」と「状態」というように分類をして、現象をモデル化するという考え方のことを状態空間モデルと呼ぶ、と考えた方がわかりよいかもしれません。
状態空間モデルでは、内部に2つの方程式をもち、その方程式をどのように定義するかによって、挙動を大きく変えることができます。
まずは、「観測値」を得る方程式から説明しましょう。
「状態」から「観測値」を得る方程式を観測方程式と呼びます。
例えば、釣り人の腕の良さによって、釣獲尾数は変わりますね。たとえ湖の中にいる魚の数「状態」が同じだったとしても、釣り人の腕によって釣獲尾数「観測値」が変わる。じゃあどのくらい、どのように変わるのかを観測方程式で指定します。
次は「状態」を得る方程式です。
「状態」は前期の「状態」から計算されます。
例えば、去年の魚の数が多ければ、親が多いわけですから子供もたくさん生まれそうですね。だから前年の魚の数「状態」が多ければ今年の魚の数「状態」も多いと計算されます。
もしも、状態空間モデルが推定できていたとしたら
状態空間モデルが推定できていたとしたら、観測方程式と状態方程式がわかっていることになりますね。
この2つを使えば、流れるように将来の「状態」と「観測値」を推定・予測することができます。
釣獲尾数を「観測値」、湖の中にいる魚の数を「状態」とする例をそのまま続けます。
以下のように将来を予測します。
2000年 2001年 2002年 ・・・
状態 10 →状態方程式→ 15 →状態方程式→ 17 ・・・
↓ ↓ ↓
観測方程式 観測方程式 観測方程式
↓ ↓ ↓
観測値 4 6 7 ・・・
状態方程式があれば、過去の「状態」から将来の「状態」を脈々と予測していくことができます。
「状態」がわかれば、そこから「観測値」の計算もできます。
もちろん将来の「観測値」がわかるのであれば、それを制御することもできるでしょう。
状態を推定するために
状態方程式と観測方程式、ひいては将来の「状態」「観測値」が推定できれば、ありがたいわけですが、これを推定するのに私たちが使うことができるのは「観測値」だけです。
だって、湖の中にいる魚の数を私たちは知らない。
というわけで、「状態」を推定する手法であるカルマンフィルタを学びましょうというお話です。
ローカルレベルモデル
観測方程式や状態方程式はいくらでも複雑にすることができます。
しかし、最初に学ぶときは簡単なものから始めたいですね。
ローカルレベルモデルは、とても単純な状態空間モデルです。
観測方程式と状態方程式は以下のようになります。
観測方程式
「観測値」 ~ 「状態」 + ノイズ
状態方程式
「状態」 ~ 「前期の状態」 + ノイズ
ノイズは、平均が0の正規分布に従います。分散は正の値であればいくつでも構いません。
難しければ「プラスになるかマイナスになるか半々の確率で発生するノイズだ」とまずは理解してください。
ノイズが乗っているものの、その期待値は0です。
ということで、観測方程式においては『観測値は状態と同じ』と計算されます。
同様に、状態方程式においては『今期の状態は、前期の状態と同じ値である』と計算されることになります。
とても単純な予測ですね。
ノイズは、平均をとると0になるのですが、各々の値は-5.01であったり+3.24であったりします。
このノイズの大きさを決めるのが分散です。
分散が大きいと、ノイズも大きくなります。例えば -30.65であったり、+54.76であったり。
分散が小さいと、ノイズも小さくなります。例えば-0.41であったり、+0.02であったり。
まずは単純なローカルレベルモデルから始めて、カルマンフィルタの計算方法を説明します。
以下の説明は、特に指定がない限り、ローカルレベルモデルを前提としていることに注意してください。
2.状態空間モデルとカルマンフィルタの関係
状態空間モデルにおいて、「状態」を効率的に推定する計算アルゴリズムが、今回の主役カルマンフィルタです。
とはいえ、カルマンフィルタだけを知っていても、実用的な状態空間モデルは推定できません。
何度も繰り返しているように、カルマンフィルタがあれば、「観測値」と観測方程式・状態方程式から「状態」を推定することができます。
しかし、カルマンフィルタの計算に用いる「パラメタ」は事前に与えなくてはなりません。
状態空間モデルを学ぶには、カルマンフィルタだけではなく、観測方程式と状態方程式を推定する方法も学ぶ必要があります。
方程式には、いくつかのパラメタが含まれます。そのパラメタを推定するのです。最尤法と呼ばれる手法を使います。
ローカルレベルモデルの場合は、とても単純な観測・状態方程式でしたが、推定すべきパラメタが0個というわけではありません。
具体的には、ノイズの大きさ、すなわちノイズの分散を推定する必要があります。
観測方程式のノイズの分散と状態方程式のノイズの分散という2つのパラメタを、最尤法という手法を使って推定します。
最尤法を使うためには「尤度」と呼ばれる指標を計算する必要があるのですが、この尤度の計算にもカルマンフィルタが一役買います。
この記事では、まずは最尤法は置いておいて、パラメタが与えられた時に、どうやって「状態」を推定していくのか、その流れを説明します。
状態空間モデルを学ぶには
1.事前にパラメタを決める方法
2.パラメタを使って、カルマンフィルタを実行し、「状態」を推定する方法
この2つのやり方を知っておく必要があるということだけご理解ください。
そして、この記事で解説するのは、2番だけです。
3.カルマンフィルタの考え方
フィルタリングして、状態推定値を修正する流れ
ローカルレベルモデルを例として、カルマンフィルタの計算の流れを説明します。
以下のような流れで計算します。
1.1期前の状態推定値を使って、次の「状態」を予測する
→これは状態方程式を使えばすぐに計算できます
2.予測された状態推定値を、当期の観測値を使って修正する
→厳密にはこれがフィルタリングです。
例を挙げます。2000年の状態が10だとわかっていたとしましょう。湖の中にいる魚の数が10尾だと推定されている、とイメージしてください。
2000年 2001年 2002年 2003年 2004年
状態 10
観測値
予測をすると、2001年の状態推定値も10だと予測されました
2000年 2001年 2002年 2003年 2004年
状態 10 → 10
観測値
しかし、2001年に釣りをすると、5尾しかいないようでした。
2000年 2001年 2002年 2003年 2004年
状態 10 → 10
観測値 5
というわけで、2001年の状態推定値を補正します。ちょっと減って、7になりました。
2000年 2001年 2002年 2003年 2004年
状態 10 → 7
観測値 5
これがフィルタリングです。
「観測値」を使って、予測された「状態」を補正していることがわかります。
次、2002年の状態を推定するときには、2001年の状態がわかっていればよいです。2000年の「観測値」や状態は全く不要です。
2001年 2002年 2003年 2004年
状態 7
観測値
あとはこの繰り返し。
観測値が来るたびに、「1期前の状態推定値から、1期後の状態推定値を予測する」という処理と「当期の観測値を使って、当期の状態推定値を修正する」という処理を逐次的に行っています。
これがカルマンフィルタでやっていることです(厳密には「当期の観測値を使って、当期の状態推定値を修正する」の部分だけがフィルタリングです)。
カルマンフィルタのキモは「当期の観測値を使って、当期の状態推定値を修正する」部分だということをまずは理解してください。
では、どのようにして補正するのでしょうか。
カルマンゲインとその計算方法
カルマンフィルタでは以下の補正の式を使います。
補正後の状態 = 補正前の状態 + カルマンゲイン ×(本物の観測値-予測された観測値)
「本物の観測値」と「予測された観測値」が大きく離れていれば、大きく補正されることがわかりますね。
気になるのはカルマンゲインです。カルマンゲインが大きければ、大きく補正されます。逆にカルマンゲインが小さければ、ほとんど補正が入らないことになります。
カルマンゲインはどのようにして求めましょうか。
「観測値」があまり「状態」と関連していないとしたら、「観測値」を基に補正をかけるのは無駄な気がしますね。
例えば、どんなに湖に魚がいなくても、なぜか魚を常にたくさん釣ってくるゴッドハンドをお持ちの方が釣りをした翌日に、管理人のような残念な釣り人が釣りをした結果を観測したならば、その釣獲尾数(観測値)を基に補正をするのはだめだとわかります。
「観測値」が「状態」とあまり関係していないとは、観測方程式におけるノイズが大きいことを意味します。
もう一つの要素が、「状態」の将来予測の精度です。
将来予測の結果があまり当たらないとわかっているならば、たくさん補正をかけた方がいいですね。
予測は当たっとるんや! という絶対の自信があれば、「本物の観測値」が「予測された観測値」と異なっていても『そんなものは観測方程式におけるノイズの範囲内なんや!』と押し通すので、補正はほとんど入りません。
というわけで、カルマンゲインは以下のように計算されます。
カルマンゲイン = 状態の予測誤差の分散 ÷(状態の予測誤差の分散+観測方程式のノイズの分散)
将来予測が当たる(「状態の予測誤差の分散」が小さい)と判断されていれば、補正は少なくなります。
また、観測方程式におけるノイズが大きいと判断されても、やはり補正幅は小さくなります。
逆に、予測なんて当たらないよ(「状態の予測誤差の分散」が大きい)あるいは「観測値」と「状態」の違いが小さい(観測方程式のノイズの分散が小さい)ならば、「本物の観測値」を信用して大きく補正されることになります。
これがカルマンフィルタの基本となる考え方です。
「状態の予測誤差の分散」の時系列変化
カルマンゲインの計算に使われる「状態の予測誤差の分散」って、どうやって判断すればいいと思いますか?
これは状態方程式におけるノイズの分散を使って計算できます。
ローカルレベルモデルの状態方程式を再掲します。
状態方程式
「状態」 ~ 「前期の状態」 + ノイズ
極端な話、状態方程式のノイズの分散が0.00001だったら、『今期の状態は、前期の状態とほとんど一緒』と判断されるため、予測の外れようがありません。
なので、この場合は、「状態の予測誤差の分散」も小さくなると考えられます。
この場合は、「観測値」が入っても、カルマンゲインが小さくなるため、ほとんど補正が入りません。
「状態」の予測誤差は、時間を経るにしたがって変化します。
例えば、明日の売り上げを予測するのと、明後日の売り上げを予測するのであれば、明日のほうが精度よく予測ができそうです。予測が長期になればなるほど、予測誤差の分散は大きくなる(予測が当たりにくくなる)ことが想像できます。
ローカルレベルモデルの場合は、シンプルに、状態方程式のノイズの分散がどんどんと足しあわされて増えていきます。
2000年の「状態」はすでに分かっており(予測誤差なし)、状態方程式のノイズの分散を1だと仮定すると、以下のようになります。
2000年 2001年 2002年 2003年 2004年
予測誤差分散 0 → 1 → 2 → 3 → 4
計算式は以下の通りです
今期の状態の予測誤差の分散 = 前期の状態の予測誤差の分散 + 状態方程式のノイズの分散
ただし、これもやはり「本物の観測値」が手に入ると、予測誤差の分散も小さくなります。
「観測値」を基にして「状態の予測誤差の分散」を修正するのも、カルマンフィルタの役割です。
具体的には、以下の計算式を用います。
補正後の状態の予測誤差の分散 =(1ーカルマンゲイン)× 補正前の状態の予測誤差の分散
カルマンゲインは、定義上、1を超えないことに注意してください。
カルマンゲインが大きいと、「状態」に大きく補正が入ります。
「状態」が正しく補正されるのですから、予測誤差の分散は小さくなるというわけです。カルマンゲインが0.9ならば、予測誤差の分散は一気に10分の1にまで減りますね。
逆に、(観測方程式のノイズの分散がとても大きいなどの理由で)カルマンゲインが0に近いならば、「状態」の補正はほとんど行われず、予測誤差の分散も大きな値のままとなってしまいます。
次からは、もう少し具体的な計算方法に移ります。
スポンサードリンク
4.ライブラリを使わないカルマンフィルタの実装
カルマンフィルタする関数の作成
特別なライブラリを使わなくても、ローカルレベルモデルくらいであれば比較的簡単に推定をすることができます。
ローカルレベルモデルを推定する関数をRで作ったので、それを参照しながら解説していきます。
ソースコードはまとめてこちらに載せてあります。
# --------------------------------------------------------------------------------------
# ライブラリを使わないカルマンフィルタの実装
# --------------------------------------------------------------------------------------
localLevelModel <- function(y, xPre, pPre, sigmaW, sigmaV) {
# お手製のカルマンフィルタ関数
# 状態の予測(ローカルレベルモデルなので、予測値は、前期の値と同じ)
xForecast <- xPre
# 状態の予測誤差の分散
pForecast <- pPre + sigmaW
# カルマンゲイン
kGain <- pForecast / (pForecast + sigmaV)
# カルマンゲインを使って補正された状態
xFiltered <- xForecast + kGain * (y - xForecast)
# 補正された状態の予測誤差の分散
pFiltered <- (1 - kGain) * pForecast
# 結果の格納
result <- data.frame(
xFiltered = xFiltered,
pFiltered = pFiltered
)
return(result)
}
実質10行ほどで計算ができますね。5行目からが実際のコードとなります。順に説明します。
5行目:関数を作成しますよという指定。
この関数では、「当期の観測値」と前期の「状態」と観測誤差・過程誤差の分散を使って、今期の「状態」を推定します。実際のフィルタリングでは、この関数を、データをずらしながら何度も使っていくことになります。
引数は以下の通りです
y :当期の観測値
xPre :前期の状態
pPre :前期の状態の予測誤差の分散
sigmaW:状態方程式のノイズの分散
sigmaV :観測方程式のノイズの分散
9行目:「前期の状態(xPre)」から「今期の状態(xForecast)」を予測する。
ローカルレベルモデルですので、予測値は前期の状態の値とまったく同じとなります。
12行目:今期の「状態の予測誤差の分散(pForecast)」の計算
以下の式に従って計算します。
今期の状態の予測誤差の分散 = 前期の状態の予測誤差の分散 + 状態方程式のノイズの分散
15行目:カルマンゲインの計算
カルマンゲインの計算式に従って求めます。
カルマンゲイン = 状態の予測誤差の分散 ÷(状態の予測誤差の分散+観測方程式のノイズの分散)
18行目:観測値とカルマンゲインから、「状態」を補正する
以下の補正式に従って計算します。
補正後の状態 = 補正前の状態 + カルマンゲイン ×(本物の観測値-予測された観測値)
21行目:カルマンゲインから、「状態の予測誤差の分散」を補正する
補正後の状態の予測誤差の分散 =(1ーカルマンゲイン)× 補正前の状態の予測誤差の分散
24行目以降:補正された「状態」と「状態の予測誤差の分散」を返す
来期以降は、この補正された値を引数にして、またこの関数を呼ぶことになります。
計算例
先ほど作った関数を、実際に使ってみましょう。
ナイル川の流量データを対象とします。
> # ナイル川流量データで計算 > Nile Time Series: Start = 1871 End = 1970 Frequency = 1 [1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994 1020 960 1180 799 958 1140 1100 [22] 1210 1150 1250 1260 1220 1030 1100 774 840 874 694 940 833 701 916 692 1020 1050 969 831 726 [43] 456 824 702 1120 1100 832 764 821 768 845 864 862 698 845 744 796 1040 759 781 865 845 [64] 944 984 897 822 1010 771 676 649 846 812 742 801 1040 860 874 848 890 744 749 838 1050 [85] 918 986 797 923 975 815 1020 906 901 1170 912 746 919 718 714 740
推定する「状態」と「状態の予測誤差の分散」を格納する入れ物を用意します。
# サンプルサイズ N <- length(Nile) # 状態の推定値 x <- numeric(N) # 状態の予測誤差の分散 P <- numeric(N)
ナイル川の流量データは1871年から存在するのですが、1871年のデータをフィルタリングするためには、前期であるところの1870年における「状態」と「状態の予測誤差の分散」が必要となります。
こういった初期値は、あらかじめ「えいや」で指定しておく必要があります。
「状態」の初期値は0に、「状態の予測誤差の分散」の初期値は1000としておきましょう。
> # 「状態」の初期値は0とします > x <- c(0, x) > x [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 [54] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 > > # 「状態の予測誤差の分散」の初期値は1000にします > P <- c(1000, P) > P [1] 1000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 [22] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 [43] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 [64] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 [85] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
先ほど作ったカルマンフィルタ関数を、全ての年に対して順繰りに実行していきます。
「状態」の初期値はx[1]に入っています。「状態の予測誤差の分散」はP[1]に入っていますね。
それと当期の観測値を使って、まずは最初のフィルタリングを行います。
補正された「状態」はx[2]に入ります。「状態の予測誤差の分散」はP[2]に入ります。
次は、その、補正された「状態」と「状態の予測誤差の分散」を引数にしてもう一度フィルタリングを行う……という流れとなります。
# カルマンフィルタの逐次計算を行う
for(i in 1:N) {
kekka <- localLevelModel(Nile[i], x[i], P[i], sigmaW = 1000, sigmaV = 10000)
x[i + 1] <- kekka$xFiltered
P[i + 1] <- kekka$pFiltered
}
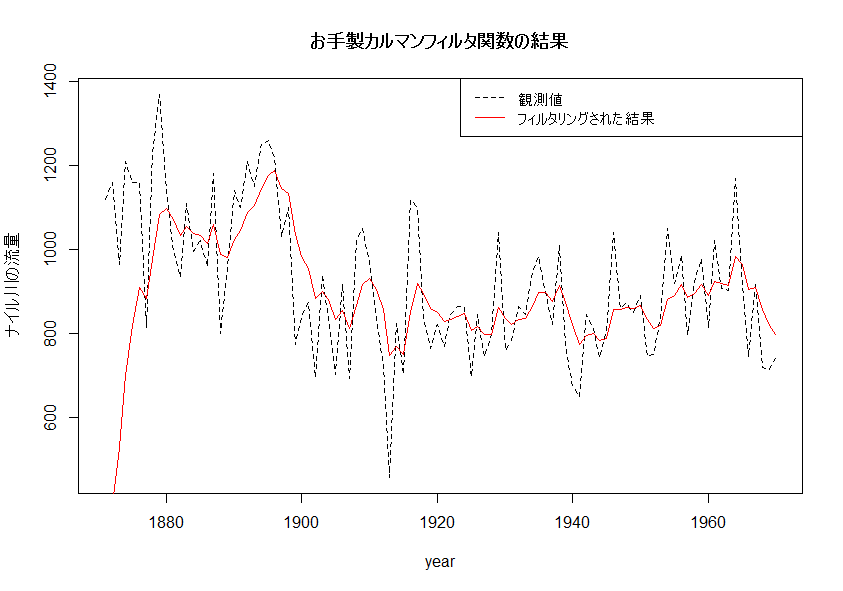
フィルタリングの結果を図示してみましょう。
推定された状態の最初の値(x[1])は、初期値ですので、使いません。x[-1]で消しておきました。
# 結果の図示
year <- 1871:1970
plot(
as.numeric(Nile) ~ year,
main="お手製カルマンフィルタ関数の結果",
ylab="ナイル川の流量",
type="l", lty=2
)
lines(x[-1] ~ year, type="l", col=2)
legend(
"topright",
legend = c("観測値", "フィルタリングされた結果"),
lty = c(2,1), col = c(1,2)
)
5.パラメタを変えたときの挙動
状態推定をする関数を作る
パラメタをいろいろ変えて計算していきますが、何度も長いコードを書くのは面倒ですね。
先ほどの計算に使ったコードをまとめて関数にしておきます。
あとは、引数のパラメタをいろいろ変えてやれば、簡単に実験ができます。
calcState <- function(data, x0, P0, sigmaW, sigmaV){
# カルマンフィルタを使って、状態を一気に推定する
# サンプルサイズ
N <- length(data)
# 状態の予測誤差の分散
P <- numeric(N)
# 「状態の予測誤差の分散」の初期値の設定
P <- c(P0, P)
# 状態の推定値
x <- numeric(N)
# 「状態」の初期値の設定
x <- c(x0, x)
# カルマンフィルタの逐次計算を行う
for(i in 1:N) {
kekka <- localLevelModel(Nile[i],x[i],P[i], sigmaW = sigmaW, sigmaV = sigmaV)
x[i + 1] <- kekka$xFiltered
P[i + 1] <- kekka$pFiltered
}
# 推定された状態を返す
return(x[-1])
}
パラメタを変えたときの挙動
色々とパラメタを変えて、状態を推定してみます。
# 最初に計算したパラメタと同じ x1 <- calcState(data=Nile, x0=0, P0=1000, sigmaW=1000, sigmaV=10000) # 「状態の予測誤差の分散」の初期値を増やした x2 <- calcState(data=Nile, x0=0, P0=100000, sigmaW=1000, sigmaV=10000) # 状態方程式のノイズの分散をとても小さくした x3 <- calcState(data=Nile, x0=1000, P0=0.1, sigmaW=0.001,sigmaV=1000000) # 観測方程式のノイズの分散をとても小さくした x4 <- calcState(data=Nile, x0=1000, P0=100000, sigmaW=10000, sigmaV=100)
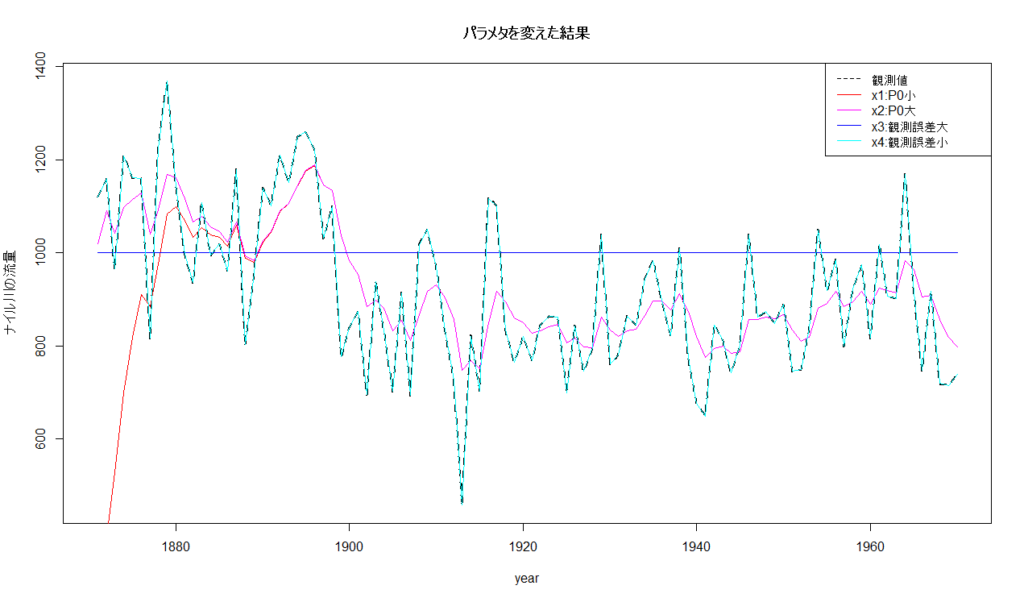
結果はこちら(画像をクリックすると大きくなります)。
点線が実際の「観測値」です。
赤い線(x1)は「状態の予測誤差の分散」の初期値が1000と小さめとなっています。なので、状態の推定を始めた直後は「状態」と「観測値」で大きなかい離が見られます。
紫の線(x2)は「状態の予測誤差の分散」の初期値を増やしました。なので、状態の推定を始めた直後から、比較的「観測値」と近い値となっています。
これは「状態の予測誤差の分散」が大きいから、予測結果は信用ならない → 大幅に状態を修正しよう! とした結果ですね。
赤い線と紫の線は、1880年台後半からほとんど同じ値となっていることに注目してください。時間をかければ、両者ともに補正が働いて、大体同じ推定結果となっていきます。
カルマンフィルタが、パラメタに対してある程度頑健であることがわかります。これは素晴らしい特徴ですね。
パラメタをうっかり変な値にしても、それほどはずれないということです。
青い線(x3)は状態方程式のノイズの分散をとても小さく、逆に観測方程式におけるノイズの分散を大きくしています。
なお、「状態」の初期値には1000を指定してあります。
すると、時間がたって、どれだけ「観測値」が増えたとしても、「状態」の推定値はずっと1000(初期値)のままとなります。
観測誤差が大きいから、「観測値」は一切信用しない。なので、「状態」の値は初期値からほぼまったく補正がなされないままとなります。とんでもないパラメタにすると、こうなってしまいます。
水色の線(x4)はその逆に、観測方程式におけるノイズの分散をとても小さくしています。
すると、大きく補正が働き、推定された「状態」は、「観測値」とほとんど同じとなっています(点線と水色の線がほぼ完全に重なっている)。
「観測値」に誤差がないんだから、「状態」は「観測値」とほとんど一緒、ということになるわけです。
なお、観測方程式・状態方程式におけるノイズの分散は「最尤法」と呼ばれる手法を用いて推定されます。
しかし、「状態」の初期値や「状態の予測誤差の分散」の初期値は「えいや!」で決めてやることが多いです。
とは言え、初期値が多少違っていても、(赤の線と紫の線のように)データが増えていけば、最終的にはほぼ同じ「状態」の推定値になります。
また、こういった初期値に依存しない方法として「散漫なカルマンフィルタ」という計算方法もあります。
最尤法や散漫なカルマンフィルタについては、別の記事で解説します。
最尤法については「カルマンフィルタと最尤法」の記事を参照してください。
6.dlmパッケージを使ったカルマンフィルタ
最後に、Rのdlmパッケージを使ったカルマンフィルタの実装例を紹介します。
dlmパッケージの使い方は、詳しくは「dlmの使い方」を参照してください。
ここでは、カルマンフィルタを実行するところまでを紹介します。
# -------------------------------------------------------------------------------------- # dlmパッケージを使ったカルマンフィルタ # -------------------------------------------------------------------------------------- library(dlm) # 参考 x5 <- calcState(data=Nile, x0=0, P0=10000000, sigmaW=1000, sigmaV=10000) # dlmのパラメタの設定 modelDlm <- dlmModPoly(order=1, m0=0, C0=10000000, dW = 1000, dV = 10000) # カルマンフィルタの実行 Filter <- dlmFilter(Nile, modelDlm)
お手製のカルマンフィルタ関数と計算結果を比較してみます。
5行目:今回使用する「dlm」というパッケージを読み込みます
8行目:参考のため、自作カルマンフィルタでも計算してみました
11行目:パラメタの設定
dlmパッケージでは、『dlmModPoly(order=1』と記述することでローカルレベルモデルを推定することができます。
m0が「状態」の初期値。
C0が「状態の予測誤差の分散」の初期値
dWが状態方程式のノイズの分散
dVが観測方程式のノイズの分散
を各々表します。
14行目:指定されたパラメタを使って、カルマンフィルタを実行する
ライブラリを使った結果と、お手製関数の結果を比較します。
なお、dlmを使った場合は、状態の推定値は「m」という変数に格納されています。
また、やはり初期値が残ったままなので、最初のデータは切り落とします。
よって、『Filter$m[-1]』が、推定された「状態」を表していることに注意してください。
> # 結果の比較 > sum((Filter$m[-1] - x5)^2) [1] 1.279545e-24
10の-24乗ほどの差しかないですので、同じとみなして差し支えないでしょう。
カルマンフィルタは応用範囲の広い技術ですので、色々なプログラミング言語で実装できる(やろうと思えばExcelでもOK)ということは覚えておいて損はないかなと思います。
ローカルレベルモデル以外のモデルですと、計算が若干複雑になりますが、考え方はあまり変わりません。
ただし、行列演算が必要になる点だけ注意してください。行列演算ができるライブラリをあらかじめ探しておくといろいろ捗ります。
参考文献
タイトル・画像はAmazonへのリンクです。
|
時系列分析と状態空間モデルの基礎:RとStanによる理論と実装 このブログの管理人が書いた、時系列分析の入門書です。カルマンフィルタや散漫カルマンフィルタについての解説があります。 サポートページはこちらです。 アマゾンさんはたまに在庫切れになります。その場合は、hontoさんの利用をお願いします。
|
 |
|
カルマンフィルタの基礎 カルマンフィルタの考え方を理解したければ、まずはこの一冊がおすすめです。 数式は多めですが、数値例も豊富です。検算ができるのが嬉しいですね。 |
 |
|
カルマンフィルタ ―Rを使った時系列予測と状態空間モデル― 薄い本ですが、内容は濃いです。数式だけでなくR言語を使った解説があるのがポイント。 この手の薄い本はえげつないくらい数式が多いのがたまにあるのですが、これはそこまでではありません。日本語での解説も丁寧ですのでお勧め。これも良書だと思います。 |
 |
|
状態空間時系列分析入門 このサイトでもよく紹介している状態空間モデルの入門書です。 カルマンフィルタの解説は少ないですが、状態空間モデルというモデルの考え方を解説した、初学者向けの良書です。 が、絶版になっているのかどうか知りませんが、中古価格が高騰中です。良い本なので再販してほしいのですが。。。 |
 |
スポンサードリンク
2017年04月15日:新規作成
2017年04月16日:リンクの追加など
2018年10月08日:リンクの追加など