”慣れ”の統計モデリング:Stanで推定する時変係数モデル
新規作成:2015年12月13日
最終更新:2016年9月22日
ローカルレベルモデルくらいでしたらdlmパッケージでも簡単に推定できます。
せっかくStanを使うのですから、もっと複雑なモデルを作ってみましょう。
今回は回帰係数が時間によって変化するモデルを作成します。
なお、今回の記事はちょっと複雑なモデルを作成する都合上、実験的な要素もあります。
そのため、ほかの記事に比べると、記載内容の精度が落ちております。この記事を参考にされる場合は、この点、注意してください。
すべてのコードをまとめたものはこちらにおいておきました。コピペする際はこちらを使用してください。
この記事はベイズ推定を応用して状態空間モデルを推定する一連の記事の一つです。
記事の一覧とそのリンクは以下の通りです。
・ベイズ統計学基礎
・ベイズと統計モデルの関係
・ベイズとMCMCと統計モデルの関係
・Stanによるベイズ推定の基礎
・Stanで推定するローカルレベルモデル
スポンサードリンク
目次
1.今回扱うモデルの説明
2.シミュレーションデータの作成
3.Stanによる状態空間モデルのベイズ推定
4.結果の答え合わせ
5.推定結果の図示
1.今回扱うモデルの説明
Stanによる状態空間モデル推定の応用編として、今回は“慣れ”をモデリングします。
最初は効果があったのに、時間がたつにつれて効果が薄くなってくること、よくありますよね。
その「時間がたつにつれて効果が薄くなる」ことを統計モデルで表します。
具体的には、「回帰係数が時間によって変化する」統計モデルを作ります。
例えば、血圧を下げる薬があったとします。
血圧 ~ 切片 + 回帰係数×薬
上記の式は普通に回帰分析をすれば推定できるのですが、この回帰係数を時間によって変化するようにしてやりましょう。
そうすれば「徐々に回帰係数が0に近づく→薬に慣れて効果が薄くなる」ことを表すことができます。
ローカルレベルモデルだけですとなんだかベイズ推定のありがたみがありませんでした。
Stanは本来、今回のモデルのように複雑なモデルを推定するのにつかわれるべきでしょう。
Stanを使うことによって、現象を非常に柔軟にモデリングすることができます。
Stanによるベイズ推定の優秀性を確認いただければと思います。
そして、複雑なモデルであっても、基本はローカルレベルモデルと同じだということも感じ取ってもらえれば幸いです。
2.シミュレーションデータの作成
今回は血圧を下げる薬の効果が徐々になくなる(薬に慣れてしまう)ことをモデル化します。
しかし、血圧の実データは持っていないですので、シミュレーションして作ります。
結果の見やすさのため、少々現実離れした設定にしてあります。ご容赦ください。
また、ややこしくなるのを防ぐため、収縮期血圧だけを対象としました。
ちなみに、期間は110日間。
最初の10日は薬を入れていません。
後の100日に薬を投与したという前提で進めていきます。
# ==================================================
# シミュレーションデータの作成
# 収縮期血圧をシミュレーションします
# ==================================================
# ------------------------------
# 薬を投与しなかった時の「状態」
# ------------------------------
N_NotMedicine <- 10 # 薬を投与しなかった日数
N_Medicine <- 100 # 薬を投与した日数
N <- N_NotMedicine + N_Medicine # 合計日数
muZero <- 160 # 初期の血圧の「状態」
# 血圧の「状態」のシミュレーション
mu <- numeric()
set.seed(12)
mu[1] <- rnorm(1, mean=muZero, sd=3)
for(i in 2:N) {
mu[i] <- rnorm(1, mean=mu[i-1], sd=3)
}
まずは、薬を一切投与しなかった時の血圧の値をシミュレーションしました。
ここは単純にランダムウォークを仮定しています。
この値はdlmパッケージに合わせて「mu」という名前にしています。
血圧の「状態」の初期値を160として、そこから、平均0、標準偏差3の正規分布に従う正規乱数を足し合わせています。
ランダムウォークがわからない方はこちらの記事をご覧ください。
シミュレーションの結果はこちら。
データを表示させた後に描画しました。
> mu [1] 155.5583 160.2898 157.4196 154.6596 148.6666 147.8497 146.9037 145.0189 [9] 144.6995 145.9836 143.6504 139.7688 137.4301 137.4659 137.0087 134.8983 [17] 138.4649 139.4865 141.0074 140.1275 140.7984 146.8200 149.8559 148.9485 [25] 145.8728 145.0707 144.4733 144.8667 145.3041 146.3903 148.4122 154.6283 [33] 153.0053 149.7938 148.6764 147.2210 148.0453 146.6068 149.0011 145.9878 [41] 146.3027 142.8347 144.5691 139.7823 138.8568 140.2052 137.2740 137.8440 [49] 140.0384 138.5606 138.4325 138.0945 139.4650 145.5260 142.3733 144.5773 [57] 146.1950 142.2522 141.5021 142.4447 143.6643 146.6476 149.2149 149.8063 [65] 152.3093 154.8496 160.7119 154.2642 157.1775 160.6127 159.0365 159.7875 [73] 158.4992 157.9517 157.6418 155.7402 151.9271 150.7752 152.3255 151.7916 [81] 151.8044 147.9822 147.3759 150.8693 150.7991 153.4906 152.9604 156.3015 [89] 154.6759 151.7857 152.9150 149.9610 152.6537 153.0415 156.1426 155.1157 [97] 156.4726 154.3883 153.6713 150.6494 156.4296 156.5838 161.9854 160.3310 [105] 160.6522 163.0196 162.2868 163.4394 159.9317 164.4865 > > plot(mu, type="b")
次はこの「ランダムウォークしている血圧 mu 」に薬の影響を入れていきます。
以下のようなモデルになります。
血圧 ~ 切片(ランダムウォークしている) + 傾き×薬の量
薬を使うと、血圧が下がることを想定しているので、傾きはマイナスになるはずです。
今回はさらに傾き(回帰係数)が時間によって変化するようにします。
”慣れ”をモデル化するという名目なので、薬の回帰係数が徐々に0に近づくようにしてやりましょう。
そこで、回帰係数にローカル線形トレンドモデルを用います。
ローカル線形トレンドモデルについてわからない方はこちらを参照してください。
こちらでは簡単な説明をするにとどめます。
ローカル線形トレンドモデルは、以下のように考えます。
1.薬の効果には、毎回「トレンド」の値が追加される
例:トレンドが常に「+1」のときは、薬を入れても毎日1ずつ「血圧が下がりにくくなる」ことになる
10日後には、「血圧が10下がりにくくなる」ことになる
初期に「血圧を―25する効果」があったとしたら、10日後には「血圧を―15する効果」でしかなくなっているというわけ。
これが”慣れ”ですね。
2.「薬の効果」はランダムウォークしている
3.「トレンド」の値もランダムウォークする
ランダムウォークするのは、「薬の効果」と、「薬の効果のトレンド」の2つであることに注意してください。
まずは、「薬の効果のトレンド」からシミュレーションします。
# --------------------------------------------------
# 時間によって変化する(慣れる)薬の効果のシミュレーション
# --------------------------------------------------
# 薬を使っても、徐々に血圧は下がらなくなっていく
coefMedicineTrendZero <- 0.005
# 時間的に変化する薬の効果
coefMedicine <- numeric(N_Medicine)
coefMedicineTrend <- numeric(N_Medicine)
# 薬の効果をトレンドモデルで表す
set.seed(1)
coefMedicineTrend[1] <- rnorm(1, mean=coefMedicineTrendZero, sd=0.03)
# トレンドのシミュレーション
for(i in 2:N_Medicine) {
coefMedicineTrend[i] <- rnorm(1, mean=coefMedicineTrend[i-1], sd=0.03)
}
「薬の効果のトレンド」は初期値が0.005で、そこから平均0で標準偏差0.03の正規分布に従う乱数が足しあわされていったものだと仮定しています。
どんな結果になったのか確認してみます。
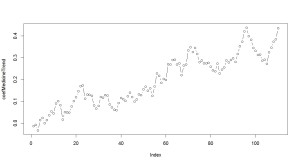
> # シミュレーション結果の確認 > > plot(coefMedicineTrend, type="b") > > sum(coefMedicineTrend) [1] 18.12397
トレンドの合計値は18です。
100日後には、「血圧が18だけ”下がりにくくなる”」ことがわかります。
本当はこんなあっけなく薬が効かなくなることはないと思います。
結果の見やすさのため、少々現実と違う前提にしてあることはご容赦ください。
次は、薬の効果のシミュレーションです。
先ほどシミュレーションされた「薬の効果のトレンド」が足しあわされていることに注意してください。
# 薬の効果のシミュレーション
# 薬の効果の初期値
coefMedicineZero <- -25
coefMedicine[1] <- rnorm(1, mean=coefMedicineTrend[1] + coefMedicineZero, sd=0.5)
for(i in 2:N_Medicine) {
coefMedicine[i] <- rnorm(1, mean=coefMedicineTrend[i] + coefMedicine[i-1], sd=0.5)
}
図示します。
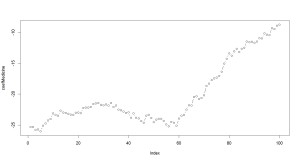
> # 図示 > > plot(coefMedicine, type="b")
最初は、薬を入れると、血圧が25も小さくなっていました。
しかし、徐々に慣れていくので、100日後には、血圧を7~8くらいしか下げる効果がないようです。
実際の薬の効果は、さらにノイズが加わると仮定しましょう。
最終的な薬の効果の時間的な変化は、以下のようになります。
# 実際の薬の効果は、さらにノイズが加わるとする
coefMedicineReal <- numeric(100)
set.seed(1)
for(i in 1:100) {
coefMedicineReal[i] <- rnorm(1, mean=coefMedicine[i], sd=2)
}
図示します。
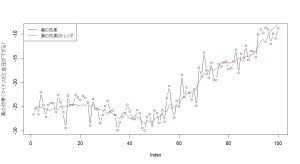
> plot(coefMedicineReal, type="b", ylab="薬の効果(マイナスだと血圧が下がる)")
> lines(coefMedicine, col=2)
> legend(
+ "topleft",
+ legend=c("薬の効果", "薬の効果のトレンド"),
+ col=c(1,2),
+ lwd=1
+ )
黒い線が、実際の薬の効果。赤い線がノイズをの取り除いた薬の効果を表しています。「トレンド」という言葉が少々紛らわしいのですが、ノイズや周期変動を取り除いた結果のこともトレンドといいます。
これでようやく「時間によって変化する薬の効果」をシミュレーションできました。
あとは、昔作った「ランダムウォークする血圧 mu」に薬の効果を足してやるだけです。
最初の10日は薬なしで、11~70日は薬あり。
効きが悪くなったので、71日後に薬の量を倍にし、101日後には初期の3倍の量にまで増やしたことにします。
# -------------------------------
# 血圧の観測値のシミュレーション
# -------------------------------
# 最初の10日は薬なし
# 70日後に薬を倍にした
# 100日後に薬を3倍にした
medicine <- c(rep(0, N_NotMedicine), rep(1, 60), rep(2, 30), rep(3, 10))
medicine
bloodPressure <- numeric(N)
bloodPressureMean <- numeric(N)
set.seed(1)
# 最初の10日は薬なし
for(i in 1:N_NotMedicine) {
bloodPressureMean[i] <- mu[i]
bloodPressure[i] <- rnorm(1, mean=bloodPressureMean[i], sd=10)
}
# 薬を投与した後の血圧のシミュレーション
for(i in (N_NotMedicine+1):N) {
bloodPressureMean[i] <- mu[i] + coefMedicineReal[i-10] * medicine[i]
bloodPressure[i] <- rnorm(1, mean=bloodPressureMean[i], sd=10)
}
どんな結果になったか、確認してみます。
薬の量を変えた日には縦線を入れておきました。
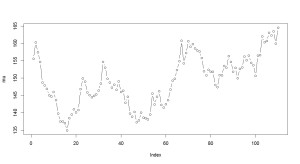
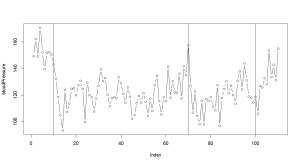
> # 実際の血圧のプロット > > plot(bloodPressure, type="b") > abline(v=10) > abline(v=70) > abline(v=100)
なんとなくそれっぽい結果になっていますね。
最初は薬を入れると、血圧がガクッと下がるんですが、徐々に血圧が上がっていきます。
薬を増やすと血圧は下がるんですが、徐々に効果がなくなっていく。
実際はここまで顕著ではないでしょうか、勉強のためのシミュレーションデータとしてはまずまずです。
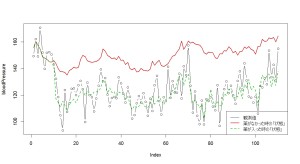
せっかくなので、「状態」の値も重ね合わせてみましょう。
> plot(bloodPressure, type="b")
> lines(mu, col=2, lwd=2)
> lines(bloodPressureMean, col=3, lty=2, lwd=2)
> legend(
+ "bottomright",
+ legend=c("観測値", "薬がなかった時の「状態」", "薬が入った時の「状態」"),
+ lwd=c(1,2,2),
+ col=c(1,2,3),
+ lty=c(1,1,2)
+ )
この緑線だの赤線だのの「状態」を今からStanを使って推定するわけです。
やってみましょう。
3.Stanによる状態空間モデルのベイズ推定
Stanでベイズ推定します。
やり方は以前と同じですので、ごく簡単に解説します。
ステップ1:Stanを使用する準備
まずは、Stanを使用する準備からです。
Stanをインストールした後に、以下を実行してください。
Stanのインストール方法などは以前の記事を参考にしてください。
#--------------------------------- # ステップ1:Stanを使用する準備 #--------------------------------- # ライブラリの読み込み require(rstan) # 計算の並列化 rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores())
ステップ2:統計モデルの記述
統計モデルに関しては、ローカルレベルモデルよりも大分と複雑になっています。
ですが、今回に限ってはそれほど難しくありません。
なぜならば、シミュレーションデータの作成とまったく同じ式を書くだけだからです。
モデルの記述は以下のようになります。
#---------------------------------
# ステップ2:統計モデルの記述
#---------------------------------
# モデルの作成
time_variant_coef <- "
data {
int N_Medicine; # 薬を投与した日数
int N; # 合計日数
vector[N] bloodPressure; # 収縮期血圧値
vector[N] medicine; # 投与した薬の量
}
parameters {
real muZero; # 血圧の「状態」の初期値
vector[N] mu; # 血圧の「状態」
real<lower=0> sigmaV; # 観測誤差の大きさ
real<lower=0> sigmaW; # 過程誤差の大きさ
real coefMedicineTrendZero; # 薬の効果のトレンドの初期値
real coefMedicineZero; # 薬の効果の初期値
vector[N_Medicine] coefMedicineTrend; # 薬の効果のトレンド
vector[N_Medicine] coefMedicine; # 薬の効果
vector[N_Medicine] coefMedicineReal; # ノイズの入った後の薬の効果
real<lower=0> sigmaWcoef; # 薬の係数の過程誤差の大きさ
real<lower=0> sigmaWcoefTrend; # 薬の係数のトレンドの過程誤差の大きさ
real<lower=0> sigmaVcoef; # 薬の係数の観測誤差の大きさ
}
model {
# 状態方程式の部分
# 血圧の状態の推定
# 左端から初年度の状態を推定する
mu[1] ~ normal(muZero, sigmaW/100);
# 血圧の状態の遷移
for(i in 2:N) {
mu[i] ~ normal(mu[i-1], sigmaW/100);
}
# 薬の効果の変化をモデル化する部分
# 初年度の薬の効果のトレンドを推定する
coefMedicineTrend[1] ~ normal(coefMedicineTrendZero, sigmaWcoefTrend/100);
# 薬の効果のトレンドの遷移
for(i in 2:N_Medicine) {
coefMedicineTrend[i] ~ normal(coefMedicineTrend[i-1], sigmaWcoefTrend/100);
}
# 初年度の薬の効果を推定する
coefMedicine[1] ~ normal(coefMedicineTrend[1] + coefMedicineZero, sigmaWcoef/100);
# 薬の効果の遷移
for(i in 2:N_Medicine) {
coefMedicine[i] ~ normal(coefMedicineTrend[i] + coefMedicine[i-1], sigmaWcoef/100);
}
# 薬の効果にノイズが入る
for(i in 1:N_Medicine) {
coefMedicineReal[i] ~ normal(coefMedicine[i], sigmaVcoef/100);
}
# 観測方程式の部分(薬なし)
for(i in 1:10) {
bloodPressure[i] ~ normal(mu[i], sigmaV/100);
}
# 観測方程式の部分(薬あり)
for(i in 11:N) {
bloodPressure[i] ~ normal(mu[i] + coefMedicineReal[i-10]*medicine[i], sigmaV/100);
}
}
"
dataブロック
data {
int N_Medicine; # 薬を投与した日数
int N; # 合計日数
vector[N] bloodPressure; # 収縮期血圧値
vector[N] medicine; # 投与した薬の量
}
dataブロックでは、サンプルサイズや血圧の値、薬の量を入れています。
parametersブロック
parameters {
real muZero; # 血圧の「状態」の初期値
vector[N] mu; # 血圧の「状態」
real<lower=0> sigmaV; # 観測誤差の大きさ
real<lower=0> sigmaW; # 過程誤差の大きさ
real coefMedicineTrendZero; # 薬の効果のトレンドの初期値
real coefMedicineZero; # 薬の効果の初期値
vector[N_Medicine] coefMedicineTrend; # 薬の効果のトレンド
vector[N_Medicine] coefMedicine; # 薬の効果
vector[N_Medicine] coefMedicineReal; # ノイズの入った後の薬の効果
real<lower=0> sigmaWcoef; # 薬の係数の過程誤差の大きさ
real<lower=0> sigmaWcoefTrend; # 薬の係数のトレンドの過程誤差の大きさ
real<lower=0> sigmaVcoef; # 薬の係数の観測誤差の大きさ
}
parametersブロックはちょっと長いんですが、ローカルレベルモデルで推定されたものと解釈は同じです。
ローカル線形トレンドモデルや時変係数モデルは、ローカルレベルモデルを足し合わせたものなので。
ちなみに、データは自分で作りましたので、正しいパラメタはわかっています。
一覧を記していおきます。
muZero:160
sigmaV:10(標準偏差です。シミュレーションの最後の段階でノイズを加えるときにsd=10と出てきています)
sigmaW:3(標準偏差です)
coefMedicineTrendZero:0.005
coefMedicineZero:-25
sigmaWcoef:0.5(標準偏差です)
sigmaWcoefTrend:0.03(標準偏差です)
sigmaVcoef:2(標準偏差です)
modelブロック
model {
# 状態方程式の部分
# 血圧の状態の推定
# 左端から初年度の状態を推定する
mu[1] ~ normal(muZero, sigmaW/100);
# 血圧の状態の遷移
for(i in 2:N) {
mu[i] ~ normal(mu[i-1], sigmaW/100);
}
# 薬の効果の変化をモデル化する部分
# 初年度の薬の効果のトレンドを推定する
coefMedicineTrend[1] ~ normal(coefMedicineTrendZero, sigmaWcoefTrend/100);
# 薬の効果のトレンドの遷移
for(i in 2:N_Medicine) {
coefMedicineTrend[i] ~ normal(coefMedicineTrend[i-1], sigmaWcoefTrend/100);
}
# 初年度の薬の効果を推定する
coefMedicine[1] ~ normal(coefMedicineTrend[1] + coefMedicineZero, sigmaWcoef/100);
# 薬の効果の遷移
for(i in 2:N_Medicine) {
coefMedicine[i] ~ normal(coefMedicineTrend[i] + coefMedicine[i-1], sigmaWcoef/100);
}
# 薬の効果にノイズが入る
for(i in 1:N_Medicine) {
coefMedicineReal[i] ~ normal(coefMedicine[i], sigmaVcoef/100);
}
# 観測方程式の部分(薬なし)
for(i in 1:10) {
bloodPressure[i] ~ normal(mu[i], sigmaV/100);
}
# 観測方程式の部分(薬あり)
for(i in 11:N) {
bloodPressure[i] ~ normal(mu[i] + coefMedicineReal[i-10]*medicine[i], sigmaV/100);
}
}
大変長くて恐縮なのですが、シミュレーションデータ作成時とほぼほぼ同じfor分が出てきているので、対応はつかめるかと思います。
ちなみに、標準偏差の値が軒並み100で割られています。これは、標準偏差がとても小さな値になることがあるからです(例えばsigmaWcoefTrendは0.03です)。
あんまりにも絶対値が小さい値を推定するのはちょっと難儀なので、補正してみました。
ですので、標準偏差に関しては、推定された値を100で割ったものが正確な標準偏差になることには注意してください。
ステップ3:データの指定
#--------------------------------- # ステップ3:データの指定 #--------------------------------- # Stanに渡すために整形 stanData <- list( N_Medicine = N_Medicine, N = N, bloodPressure = bloodPressure, medicine = medicine )
Stanに渡すデータを作ります。
結果はこんな感じ。
> stanData $N_Medicine [1] 100 $N [1] 110 $bloodPressure [1] 149.29376 162.12624 149.06329 170.61236 151.96171 139.64506 151.77799 152.40218 150.45735 [10] 142.92970 132.18367 118.46373 104.65843 93.31067 123.63889 107.33327 113.65754 124.67812 [19] 124.94871 119.98925 127.38231 130.56485 124.47869 99.67208 129.36767 119.87160 118.34687 [28] 107.56877 117.44763 126.99728 139.25371 130.45737 132.76207 120.36170 111.51491 117.68982 [37] 118.49654 117.59473 133.30827 128.76936 120.85159 114.27748 125.79208 118.61439 102.11582 [46] 104.89868 113.83460 119.18229 114.33592 121.41410 114.93621 104.41282 117.18018 107.93158 [55] 127.28805 134.48931 115.38457 105.30249 118.36619 115.33829 141.33881 117.92316 130.37528 [64] 121.97715 121.75112 136.03796 117.35701 141.73396 134.88257 157.40427 126.91868 106.69661 [73] 122.56858 104.43091 98.04414 115.83592 97.92867 116.90669 115.50529 118.28625 111.18448 [82] 108.59336 127.31302 96.77801 117.68534 124.36536 130.21267 121.44288 126.97684 119.99539 [91] 113.42024 130.58334 137.87064 124.13684 143.85829 130.96815 118.91190 117.93367 114.39183 [100] 118.68522 105.98207 126.75058 125.77507 132.67392 128.02486 153.50165 133.45262 142.71959 [109] 131.06140 154.86355 $medicine [1] 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 [47] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 [93] 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3
ステップ4:ベイズ推定の実行
ベイズ推定します。
ちなみに、この計算は、管理人のPCで2.5時間ほどかかりました。
お出かけ前や、寝る前に計算されることをお勧めします。
#---------------------------------
# ステップ4:ベイズ推定の実行
# 注意。相当時間がかかります(2時間以上)
#---------------------------------
# 乱数の種
set.seed(1)
# ローカルレベルモデル
time_variant_coef_Model_1 <- stan(
model_code = time_variant_coef,
data=stanData,
iter=45000,
warmup=35000,
thin=10,
chains=3,
control=list(
adapt_delta=0.9,
max_treedepth=13
)
)
# 警告メッセージが出てしまいますが、今回はそのまま使いました(本当はあまりよくはありません)。
# 警告メッセージ:
#1: There were 26 divergent transitions after warmup. Increasing adapt_delta may help.
#2: There were 70 transitions after warmup that exceeded the maximum treedepth. Increase max_treedepth.
#3: Examine the pairs() plot to diagnose sampling problems
コメントにも書いたのですが、警告メッセージが出てしまいました。
警告が出ないようにとcontrolを追加したのですが、ちょっとうまくいかなかったのでそのまま載せています。
本当はあまりよくないのですが、今回は答えがわかっているデータを相手にして、答え合わせができますので、そのままにしておいています。
今後、警告が出ないようなパラメタの設定(あるいはモデル式の修正)ができれば追記いたします。
4.結果の答え合わせ
> #---------------------------------------
> # ステップ5:うまく推定されているかをチェック~修正
> #---------------------------------------
>
> # 結果の確認
> # 推定されたパラメタ
> time_variant_coef_Model_1
Inference for Stan model: 99781873c16b815690901921a0596860.
3 chains, each with iter=45000; warmup=35000; thin=10;
post-warmup draws per chain=1000, total post-warmup draws=3000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
muZero 153.11 0.11 4.84 144.07 150.08 153.01 156.08 162.87 1796 1.00
mu[1] 153.10 0.10 4.17 145.07 150.37 153.04 155.71 161.62 1721 1.00
mu[2] 153.33 0.12 3.89 146.13 150.74 153.27 155.94 161.27 1077 1.00
mu[3] 153.17 0.10 3.66 146.14 150.79 153.23 155.52 160.32 1255 1.00
・・・以下略
ちょっとえげつない量の結果が出てくるのですが、とりあえずRhat<1.1は満たされているようです。
ちなみに、traceplotを見ると、やはりあまりきれいな結果にはなっていませんでした。
本当は修正が必要なのでしょうが、今回はそのまま進めます。
推定されたパラメタの答え合わせをします。
> print(summary(time_variant_coef_Model_1)$summary,3)
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
muZero 153.113 0.1142 4.839 144.070 150.079 153.015 156.080 162.87 1795.9 1.00
sigmaV 924.473 3.2399 94.811 743.925 863.324 923.349 983.602 1118.55 856.4 1.00
sigmaW 186.121 12.6175 122.252 20.032 90.726 167.359 258.103 478.79 93.9 1.03
coefMedicineTrendZero 0.137 0.0174 0.678 -1.396 -0.143 0.198 0.464 1.42 1519.6 1.00
coefMedicineZero -34.003 0.2070 7.331 -47.452 -38.954 -34.199 -29.306 -18.65 1253.8 1.01
sigmaWcoef 150.506 6.3552 87.099 20.649 82.797 141.705 207.776 343.52 187.8 1.01
sigmaWcoefTrend 12.742 1.3239 12.331 0.772 4.317 8.944 16.770 47.84 86.7 1.05
sigmaVcoef 170.677 15.1781 109.016 12.247 86.179 154.160 239.318 416.03 51.6 1.05
>
ちなみに、答えは以下の通りです。95%区間には一応入っているようです(標準偏差はすべて100で割らなければいけないことに注意してください)。
muZero:160
sigmaV:10(標準偏差です。シミュレーションの最後の段階でノイズを加えるときにsd=10と出てきています)
sigmaW:3(標準偏差です)
coefMedicineTrendZero:0.005
coefMedicineZero:-25
sigmaWcoef:0.5(標準偏差です)
sigmaWcoefTrend:0.03(標準偏差です)
sigmaVcoef:2(標準偏差です)
とりあえず、答えとそこまでかい離していなかったので、そのまま続けます。
5.推定結果の図示
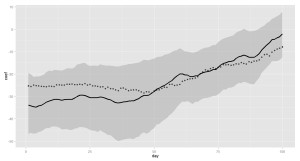
時間的に変化する回帰係数を図示します。
まずは、係数の95%区間をとります。
# 係数の時間的変化 coefEAP <- summary(time_variant_coef_Model_1)$summary coefLower95 <- summary(time_variant_coef_Model_1)$summary coefUpper95 <- summary(time_variant_coef_Model_1)$summary
後は、ggplot2を使って図示します。
実際の回帰係数(答え)を点線で表示するようにしました。
# 係数の変化の図示
library("ggplot2")
# 描画したいデータをまとめる
d1 <- data.frame(day=1:100, coef=coefMedicine[1:100])
d2 <- data.frame(day=1:100, EAP=coefEAP , lower=coefLower95, upper=coefUpper95)
head(d1)
head(d2)
# グラフの外枠の作成
coefGraph <- ggplot(
data=d1,
aes(
x=day,
y=coef
)
)
# データ点を追加
coefGraph <- coefGraph + geom_point()
# EAP推定量と95%信用区間を追加
coefGraph <- coefGraph + geom_smooth(
aes(
ymin=lower, ymax=upper, y=EAP
),
lwd=1.2,
color=1,
data=d2,
stat="identity"
)
# 描画
plot(coefGraph)
時間がたつにつれて、血圧が下がりにくい(回帰係数が0に近づく)ことがわかります。
答えも、一応95%信用区間には含まれているようです。
今回は若干荒いところもありましたが、複雑なモデルを推定する雰囲気が伝わればと思います。
パラメタの収束が悪かった件に関しては、パラメタの事前分布を変えるなど、いろいろのやり方が考えられます。
今後、追記、修正していく予定です。
参考文献
|
基礎からのベイズ統計学: ハミルトニアンモンテカルロ法による実践的入門 何度も紹介していますが、ベイズ推定について書かれた良書です。 巻末の付録にStanの使い方も書かれています。 |
 |
|
岩波データサイエンス Vol.1 特集「ベイズ推論とMCMCのフリーソフト」 こちらも何度も紹介している本です。 ソフトの使い方に関しては、こちらのほうが詳しいです。 状態空間モデルは、季節調整モデルなどの解説があります。 |
 |
スポンサードリンク


馬場様
いつも勉強させていただいております。特に状態空間モデルの説明は、他のサイトで数式に圧倒されて気力をそがれていたのですが、このサイトを入り口としてまずはイメージをつかむところから始めています。
今回、Stanを用いて回帰係数が時々刻々と変化するモデルの作り方を紹介されていますが、このときのカルマンフィルターやスムージングとの関係はどうなるのでしょうか?以前の記事で状態空間モデルの流れは以下の4Stepだと説明されているのをお見かけいたしました。
Step1 状態空間モデルの「型」を決める
Step2 その「型」にいれるパラメタを推定する
Step3 Step2で推定されたパラメタを「型」に入れてカルマンフィルターを回す
Step4 カルマンフィルターの結果を使ってスムージングする
ですが、今回の記事ではStep2 のパラメタを推定するところでとまっているように感じてしまいました。何かカルマンフィルターやスムージングの概念を勘違いしていますでしょうか?時変係数のモデルだけでなくローカルレベルモデルの場合でもそう感じていました。
yamamoto様
コメントありがとうございます。
少々時間がかかってしまいましたが、回答用のページを書いてみました。
よろしければ、ご参照ください。
http://logics-of-blue.com/%E7%8A%B6%E6%85%8B%E7%A9%BA%E9%96%93%E3%83%A2%E3%83%87%E3%83%AB%E3%81%AE%E6%8E%A8%E5%AE%9A%E6%96%B9%E6%B3%95%E3%81%AE%E5%88%86%E9%A1%9E/
よろしくお願いします。
馬場様
大変ためになる資料の数々,誠にありがとうございます。このサイトにはいつも助けられております。
一点ご質問させていただきたいのですが,時変係数モデルでは,外生変数から観測値への影響に時間的なラグがある場合のモデルを作ることは可能でしょうか?
薬の例ですと,飲んだ当日には血圧に影響はないが,翌日から効いてくるといった想定です。さらに,その効果は三日後まで減衰しながら継続するという状況なども考えられると思います(推定するパラメータ数が非常に多くなるように思いますが…)
ご説明の内容を勘違いしていたら申し訳ありません。
お忙しいところ恐縮ですがご返信いただければ幸いです。
藤川様
コメントありがとうございます。
管理人の馬場です。
> 外生変数から観測値への影響に時間的なラグがある場合のモデルを作ることは可能でしょうか?
もちろん可能だと思います。一番単純なやり方は、ラグを取った説明変数を使うことでしょうか(1日前の薬の服用の有無を説明変数として使う)。
あるいは薬を飲んだ後の5日ほど連続で「薬を飲んだ直後フラグ」を1とした説明変数を入れる方法もあるかもしれません(薬を飲んだ直後以外はフラグは0)。
「広告の効果が徐々に減衰する」のと似たような形で「薬の効果が徐々に減衰する」のを表現できるかもしれません。ただ、広告と違ってフラグを入れる期間を恣意的に決めざる負えないのが難しいところですね。
馬場様
早速のお返事,また丁寧なご回答誠にありがとうございます。
こちらで操作した変数からの影響,つまり伝達関数のようなものが算出できないだろうかと考えていたのですが,「薬を飲んだ直後フラグ」が近いように思います。
(時変係数ではないですが。。。)
非常に参考になりました。ありがとうございます。
今後のブログ更新も楽しみにしております。