Stanで推定するローカルレベルモデル
新規作成日:2015年12月6日
最終更新日:2016年9月22日
Stanを使って、ローカルレベルモデルを推定しましょう。
今回はナイル川の流量データを対象として、ローカルレベルモデルを推定します。
なお、Stanとベイズ推定の基礎に関しては、以下の記事をご覧ください
ベイズ統計学基礎
ベイズと統計モデルの関係
ベイズとMCMCと統計モデルの関係
Stanによるベイズ推定の基礎
状態空間モデルの基礎に関しては、以下の記事をご覧ください
状態空間モデルとは
dlmの使い方(Stanを使わないで状態空間モデルを推定する方法について書いてあります)
ローカルレベルモデル
季節とトレンド
コードをまとめたものはこちらにおいておきます。コピペする際はこちらをお使いください。
スポンサードリンク
目次
1.ローカルレベルモデルとは
2.状態空間モデルの「左端」の問題
3.Stanによるローカルレベルモデルの推定
4.推定結果の取得と利用方法
おまけ1.ggplot2を使ったきれいなグラフを作る
おまけ2.乱数の一覧を取得する方法
おまけ3.結果の保存
1.ローカルレベルモデルとは
ローカルレベルモデルについては、それだけで一つの記事を書いていますので、こちらをご覧ください。
ここでは簡単な紹介をするにとどめます。
状態空間モデルはその名の通り「状態」を推定します。
私たちが手に入れたデータは「観測」結果として「状態」とは明確に区別します。
状態の変化の仕方を表す部分を「状態方程式」と呼びます。
状態から観測データが得られるプロセスを表す部分を「観測方程式」と呼びます。
ローカルレベルモデルは、「状態」の変化の仕方をランダムウォークだと仮定します。
「観測」の結果は、「状態」に正規分布に従うノイズが加わったものだと仮定します。
なので、ローカルレベルモデルは、別名「ランダムウォーク・プラス・ノイズ モデル」と呼ばれます。
ランダムウォークに従って遷移する「状態」にノイズが加わって「観測」データが得られると仮定しているからです。
ランダムウォークとは、「一期前の値からスタートしてノイズを付け加えていった結果」だと思っていただければ結構です。
一回のノイズはあまり大きな値をとらないかもしれません。でも、ノイズが累積されていくと、大きな変化を生み出す時があります。
例えばノイズが「1,2,1,-1,3」だとしましょう。
「一期前の値からスタートしてノイズを付け加えていった結果」は以下のようになります
1
↓
1+2 = 3
↓
3+1 = 4
↓
4-1 = 3
↓
3+3 = 6
というわけで、ノイズの累積和は「1,3,4,3,6」ですね。
一つ一つのノイズを見ると最大値は3なのですが、累積和をとるとどんどん大きくなっていくこともあります。
もちろん、負のノイズが累積されると、どんどん小さな値になっていくこともあり得ます。
私たちの目に見えない「状態」にランダムウォークを仮定し、その「状態」にノイズが付け加わったものが「観測」データです。
「状態」に付け加わるノイズのことを「過程誤差」と呼びます。
「観測」が得られる際に入るノイズのことを「観測誤差」と呼びます。
今回は、「過程誤差」も「観測誤差」も平均値が0の正規分布に従うホワイトノイズだと仮定します。
よって、「過程誤差」と「観測誤差」の分散の値が推定できれば、ローカルレベルモデルが推定できることになります。
2.状態空間モデルの「左端」の問題
状態空間モデルを推定するにあたって、悩ましいのが「左端」の存在です。「左端」は私の造語ですが、ほかの言い方が難しいですのでそのまま使っています。よい用語があれば教えてください。
ランダムウォークとは、「一期前の値からスタートしてノイズを付け加えていった結果」です。
今回はナイル川の流量データをモデリングします。
ナイル川の流量データは1871年から1970年まで、100年間分のデータがあります。
ランダムウォークしていると仮定する以上、1970年の「状態」は、1969年の「状態」に過程誤差が加わって生成されますね。
1969年の「状態」は1968年の「状態」に過程誤差が加わって生成されます。
それをずーっと戻していきます。
1872年の「状態」は1871年の「状態」に過程誤差が加わって生成されます。
では、初年度である1871年の「状態」は、いったいどこから推定すればよいのでしょう。1870年のデータは存在しないのに。
1870年の「観測」データは存在しないんですけど、1870年の「状態」は計算できなきゃ困ります。
というわけで、1870年の「状態」をこの記事では「左端」と呼んで、別途推定することにします。
この「左端」もStanを使えばちゃんとベイズ推定できますので心配はいりません。
とはいえ、コードを理解するためには、「左端」の存在を理解しなければいけないですので、ここで補足しておきました。
3.Stanによるローカルレベルモデルの推定
Stanを使って、ローカルレベルモデルを推定してみます。
コードをまとめたものはこちらにおいておきます。コピペする際はこちらをお使いください。
Stanの基礎やインストールの方法についてはこちらを参照してください。
以下の5つのステップを踏んで、モデルを推定します。
ステップ1:Stanを使用する準備
ステップ2:統計モデルの記述
ステップ3:データの指定
ステップ4:ベイズ推定の実行
ステップ5:うまく推定されているかをチェック~修正
順にみていきます。
ステップ1:Stanを使用する準備
Stanがインストールできていれば、ライブラリを読み込むだけでOKです。
計算の並列化も試してみます。
#--------------------------------- # ステップ1:Stanを使用する準備 #--------------------------------- # ライブラリの読み込み require(rstan) # 計算の並列化 rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores())
ステップ2:統計モデルの記述
ローカルレベルモデルは、以下のように記述します。
#---------------------------------
# ステップ2:統計モデルの記述
#---------------------------------
# モデルの作成
localLevelModel_2 <- "
data {
int n; # サンプルサイズ
vector[n] Nile; # ナイル川の流量データ
}
parameters {
real muZero; # 左端
vector[n] mu; # 確率的レベル
real<lower=0> sigmaV; # 観測誤差の大きさ
real<lower=0> sigmaW; # 過程誤差の大きさ
}
model {
# 状態方程式の部分
# 左端から初年度の状態を推定する
mu[1] ~ normal(muZero, sqrt(sigmaW));
# 状態の遷移
for(i in 2:n) {
mu[i] ~ normal(mu[i-1], sqrt(sigmaW));
}
# 観測方程式の部分
for(i in 1:n) {
Nile[i] ~ normal(mu[i], sqrt(sigmaV));
}
}
"
上記のコードをもう少し詳しく見ていきます。
dataブロック
data {
int n; # サンプルサイズ
vector[n] Nile; # ナイル川の流量データ
}
データのブロックについては、特に複雑な指定はありません。
サンプルサイズと、ナイル川の流量データを指定しているだけです。
「intってなんやねん」という方はこちらをご覧ください。
parameters
parameters {
real muZero; # 左端
vector[n] mu; # 確率的レベル
real<lower=0> sigmaV; # 観測誤差の大きさ
real<lower=0> sigmaW; # 過程誤差の大きさ
}
ローカルレベルモデルの場合、推定するのは大きく2つあります。
1つは、「状態」の値そのもの。
1つは、過程誤差や観測誤差の分散の大きさです。
2,3行目が「状態」を表すパラメタです。
muZeroが「左端」すなわち1871年からしかないナイル川流量データの1870年時点の「状態」を表すパラメタです。
次のmuが100年間分の「状態」の推定値です。
4,5行目が過程誤差や観測誤差の分散です。
sigmaVが観測誤差、sigmaWが過程誤差の分散です。
VやWといった命名はdlmパッケージに合わせました。
model
model {
# 状態方程式の部分
# 左端から初年度の状態を推定する
mu[1] ~ normal(muZero, sqrt(sigmaW));
# 状態の遷移
for(i in 2:n) {
mu[i] ~ normal(mu[i-1], sqrt(sigmaW));
}
# 観測方程式の部分
for(i in 1:n) {
Nile[i] ~ normal(mu[i], sqrt(sigmaV));
}
}
modelブロックは少々複雑なので、上から順を追って解説します。
まずはナイル川の流量の初年度のデータ、1871年の話から始めましょう。
最初の状態、すなわち1番目のmuは、1870年の「状態」であるmuZero(「左端」のことですね)に過程誤差が加わって生成されます。
よって、4行目では「期待値muZero、分散sigmaWに従う正規分布」に従って1871年の状態(mu[1])が得られると指定しています。
「分散sigmaWの過程誤差が加わる」動作が「期待値muZero、分散sigmaWの正規分布に従う乱数を発生させる」ことと同じだということはイメージがわくでしょうか。
過程誤差は、期待値0のホワイトノイズです。
加えられる過程誤差の期待値が0なので、「過程誤差が加わった結果の期待値」は、過程誤差が加わる前の値(muZero)と変わりがありません。
ということで、期待値に1年前の状態であるmuZeroが入るのでした。
8行目に書かれた次の状態の遷移は、初年度(1871年)の状態推定においては無視します。
だって、muZeroから状態がすでに遷移しているから。
forループの中が(i in 2:n)と「2」からスタートしていることに注意してください。
そして13行目に移り、初年度の「状態」であるmu[1]に観測誤差が加わって、初年度の「観測」であるNile[1]が得られます。
これも、観測誤差の期待値が0であるため、「期待値mu[1]、分散sigmaVに従う正規分布」に従って「観測」データが得られると記述してあることに注意してください。
次は2年目です。
2年目の「状態」の推定値mu[2]は、1年前の状態の推定値mu[1]に過程誤差が加わって生成されます。
これは、8行目に記述されています。
「mu[i] ~ normal(mu[i-1], sqrt(sigmaW));」により、「 i 年目の状態は、期待値が『 i-1 年目の状態』で分散が sigmaW の正規分布に従う」ことを指定しています。1年前の状態から当年の状態へ遷移しています。これが2年目以降ずっと続きます。
「観測」については、初年度と変わらず、「 i 年目の観測データは、期待値が『同じ年(i 年)の状態』で分散が sigmaV の正規分布」に従います。
これを100年間ループ(サンプルサイズnには100を指定する予定です)すれば、すべての年で「状態」が推定できます。
ステップ3:データの指定
データには、Rにもともと入っているナイル川流量データを使います。
> #--------------------------------- > # ステップ3:データの指定 > #--------------------------------- > # Nile川流量データ > Nile Time Series: Start = 1871 End = 1970 Frequency = 1 [1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994 [15] 1020 960 1180 799 958 1140 1100 1210 1150 1250 1260 1220 1030 1100 [29] 774 840 874 694 940 833 701 916 692 1020 1050 969 831 726 [43] 456 824 702 1120 1100 832 764 821 768 845 864 862 698 845 [57] 744 796 1040 759 781 865 845 944 984 897 822 1010 771 676 [71] 649 846 812 742 801 1040 860 874 848 890 744 749 838 1050 [85] 918 986 797 923 975 815 1020 906 901 1170 912 746 919 718 [99] 714 740
これをStanに渡すために整形します。
> # Stanに渡すために整形 > NileData <- list(Nile = as.numeric(Nile), n=length(Nile)) > NileData $Nile [1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994 [15] 1020 960 1180 799 958 1140 1100 1210 1150 1250 1260 1220 1030 1100 [29] 774 840 874 694 940 833 701 916 692 1020 1050 969 831 726 [43] 456 824 702 1120 1100 832 764 821 768 845 864 862 698 845 [57] 744 796 1040 759 781 865 845 944 984 897 822 1010 771 676 [71] 649 846 812 742 801 1040 860 874 848 890 744 749 838 1050 [85] 918 986 797 923 975 815 1020 906 901 1170 912 746 919 718 [99] 714 740 $n [1] 100
ステップ4:ベイズ推定の実行
stan関数を使って、ベイズ推定を実行します。
#--------------------------------- # ステップ4:ベイズ推定の実行 #--------------------------------- # 乱数の種 set.seed(1) # ローカルレベルモデル Nile_LocalLevelModel_1 <- stan( model_code = localLevelModel_2, data=NileData, iter=2500, warmup=1000, thin=1, chains=3 )
model_codeはStep2で作成されたモデル式を、dataにはStep3で整形されたナイル川流量データを指定します。
1回のシミュレーションの繰り返し数(iter)は2500とし、最初の1000個のシミュレーション結果は使用せずに捨てます(warmup=1000)。
間引きはせず(thin=1)、2500回のシミュレーションを3回繰り返します(chains=3)。
ステップ5:うまく推定されているかをチェック~修正
推定されたパラメタを表示するには、以下のコードを実行します。
#--------------------------------------- # ステップ5:うまく推定されているかをチェック~修正 #--------------------------------------- # 結果の確認 # 推定されたパラメタ Nile_LocalLevelModel_1
今回は状態を100年間も推定したので、100以上パラメタがあります。少々長いので、ここでは省略します。
過程誤差と観測誤差の分散が正しく推定されているかを確認します。
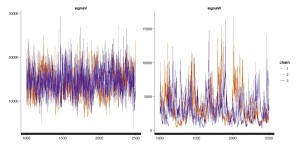
# 計算の過程を図示
traceplot(Nile_LocalLevelModel_1, pars=c("sigmaV", "sigmaW"))
引数「pars」を指定すると、特定のパラメタだけを表示させることができます。
推定結果が多い時はここを指定しないと、ほしい結果が出てきません。
グラフを見ると、難しいところですがsigmaWがあまりきれいではありませんね。
きれいかどうかの判別って難しいんですが、各々のChainがまんべんなく混ざり合っている状態が理想です。
Rhatは1.1以下であり、そこまで問題はないかと思いますが、念のためシミュレーションをやり直します。
# 乱数の種 set.seed(1) # ローカルレベルモデル Nile_LocalLevelModel_2 <- stan( model_code = localLevelModel_2, data=NileData, iter=30000, warmup=1000, thin=10, chains=3 )
繰り返し数(iter)を増やしたうえで、シミュレーション結果の間引きを行いました。
繰り返し数を増やすと計算に時間がかかるのが難ですが、実務の際は解析にかけられる時間などスケジュールと相談して実行してください。
以前にも書きましたが、ベイズ推定を行う際は短いスケジュールでやるべきではないと思います。
(ローカルレベルモデルくらいなら数分で終わりますが)
過程誤差と観測誤差の分散をもう一度確認します。
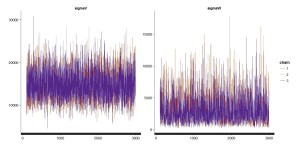
# 計算の過程を図示
traceplot(Nile_LocalLevelModel_2, pars=c("sigmaV", "sigmaW"))
こっちのほうが、各chainごとにきれいに混ざり合っていてよさそうです。
ちなみにRhatはぴったり1になっています(無理にぴったり1にする必要はないのですが)。
長くて恐縮なのですが、こちらは結果をすべて表示させておきます。
> # 結果の確認
> # 推定されたパラメタ
> Nile_LocalLevelModel_2
Inference for Stan model: 7ff087465501d18de61369d0a685dd45.
3 chains, each with iter=30000; warmup=1000; thin=10;
post-warmup draws per chain=2900, total post-warmup draws=8700.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
muZero 1112.39 1.00 87.14 943.32 1054.26 1112.00 1167.67 1287.80 7556 1
mu[1] 1111.59 0.78 68.72 980.27 1065.45 1110.79 1156.83 1247.45 7768 1
mu[2] 1110.25 0.65 60.79 992.69 1069.50 1108.96 1150.49 1231.59 8700 1
mu[3] 1099.69 0.62 57.67 986.65 1060.69 1099.65 1138.50 1211.58 8586 1
mu[4] 1117.48 0.64 56.58 1007.99 1080.13 1116.66 1155.07 1231.14 7840 1
mu[5] 1115.75 0.64 55.67 1008.99 1078.79 1114.88 1152.25 1228.77 7485 1
mu[6] 1106.98 0.59 55.01 997.78 1070.36 1107.10 1143.76 1215.57 8690 1
mu[7] 1086.00 0.63 55.86 971.33 1049.90 1086.86 1123.93 1193.53 7827 1
mu[8] 1121.82 0.68 56.30 1017.97 1083.49 1119.37 1158.10 1239.09 6897 1
mu[9] 1136.36 0.81 60.86 1026.56 1094.65 1131.87 1174.33 1268.21 5613 1
mu[10] 1105.77 0.64 55.15 999.09 1068.70 1104.84 1141.70 1218.20 7522 1
mu[11] 1070.15 0.58 53.11 963.56 1035.50 1070.60 1105.27 1174.51 8328 1
mu[12] 1048.77 0.65 55.02 936.76 1013.00 1050.75 1086.05 1152.41 7227 1
mu[13] 1050.20 0.59 53.84 942.57 1014.49 1051.18 1086.22 1154.60 8254 1
mu[14] 1037.36 0.61 54.87 925.11 1001.65 1038.82 1074.39 1140.81 8095 1
mu[15] 1033.31 0.59 54.46 920.77 998.24 1034.87 1069.73 1137.56 8501 1
mu[16] 1029.38 0.65 54.33 914.97 994.25 1031.56 1066.79 1130.66 7004 1
mu[17] 1038.93 0.58 53.38 934.60 1002.98 1039.62 1075.24 1140.83 8402 1
mu[18] 1016.41 0.75 58.53 893.57 979.66 1018.95 1056.56 1121.97 6030 1
mu[19] 1037.91 0.63 55.89 921.23 1001.85 1039.77 1075.21 1143.52 7983 1
mu[20] 1074.09 0.59 54.06 968.45 1037.72 1073.81 1108.80 1185.42 8435 1
mu[21] 1098.10 0.68 55.51 994.01 1060.71 1096.46 1133.84 1213.60 6645 1
mu[22] 1122.35 0.82 59.59 1011.51 1081.35 1119.99 1160.69 1246.16 5265 1
mu[23] 1130.77 0.87 61.69 1016.89 1087.12 1128.85 1171.59 1257.37 4986 1
mu[24] 1139.22 1.04 66.46 1018.07 1091.87 1136.74 1183.63 1274.09 4078 1
mu[25] 1129.72 1.04 66.78 1007.61 1083.02 1128.10 1173.50 1267.76 4154 1
mu[26] 1099.50 0.96 62.20 984.02 1057.01 1096.34 1140.16 1229.95 4220 1
mu[27] 1047.44 0.68 56.27 940.79 1009.46 1046.16 1082.98 1161.71 6863 1
mu[28] 1002.83 0.59 54.66 896.29 966.41 1001.88 1038.28 1111.67 8696 1
mu[29] 937.37 0.70 57.03 819.26 901.42 939.65 976.58 1042.21 6593 1
mu[30] 904.59 0.77 57.99 782.03 868.00 906.99 944.87 1010.07 5688 1
mu[31] 881.36 0.79 58.84 760.41 842.44 883.94 922.17 990.95 5550 1
mu[32] 856.50 0.87 60.19 731.15 816.55 858.93 898.22 968.96 4745 1
mu[33] 863.31 0.69 55.99 748.74 826.96 864.51 902.01 968.27 6620 1
mu[34] 851.10 0.73 56.82 736.44 813.71 852.83 890.01 957.32 5988 1
mu[35] 840.02 0.77 57.85 722.58 802.41 842.36 879.12 948.36 5698 1
mu[36] 854.80 0.63 55.06 744.41 818.87 856.08 891.87 960.16 7611 1
mu[37] 853.45 0.65 54.90 742.85 816.79 854.11 890.39 959.54 7233 1
mu[38] 887.47 0.65 56.14 781.53 849.21 886.37 924.19 999.96 7357 1
mu[39] 896.29 0.74 59.10 785.60 855.88 893.82 933.95 1020.00 6385 1
mu[40] 874.94 0.65 56.05 769.71 836.74 873.89 911.28 988.90 7500 1
mu[41] 836.55 0.59 54.78 726.03 800.07 836.83 873.16 942.70 8695 1
mu[42] 798.26 0.76 59.81 674.16 760.46 800.26 838.93 909.11 6223 1
mu[43] 770.88 1.03 68.53 622.72 728.22 776.08 818.30 891.43 4451 1
mu[44] 805.35 0.70 57.28 685.91 768.56 807.17 844.72 912.86 6732 1
mu[45] 832.02 0.61 54.78 721.12 795.65 833.26 868.55 938.87 8153 1
mu[46] 886.86 0.79 60.71 777.84 844.27 883.90 924.82 1015.57 5845 1
mu[47] 894.59 0.89 63.00 782.57 851.28 890.41 932.79 1029.29 5024 1
mu[48] 862.07 0.62 55.11 756.77 824.59 860.68 898.36 974.57 7837 1
mu[49] 838.90 0.60 54.40 730.65 803.65 838.73 874.90 946.10 8321 1
mu[50] 831.08 0.59 54.41 720.98 795.93 831.80 867.77 936.17 8575 1
mu[51] 823.91 0.59 54.60 712.41 788.52 824.73 860.32 930.21 8644 1
mu[52] 828.76 0.58 54.25 720.99 792.81 829.02 864.20 935.70 8668 1
mu[53] 830.20 0.59 54.05 722.82 794.16 830.61 866.12 937.24 8449 1
mu[54] 823.92 0.60 54.68 713.30 788.74 825.42 859.65 929.06 8229 1
mu[55] 809.64 0.65 55.53 694.33 773.37 812.13 847.57 911.84 7199 1
mu[56] 817.28 0.64 55.40 704.18 781.43 818.18 854.55 923.22 7557 1
mu[57] 817.81 0.64 54.87 704.73 782.90 818.86 854.88 921.81 7373 1
mu[58] 833.01 0.58 53.63 727.17 798.15 833.59 867.86 938.36 8482 1
mu[59] 855.65 0.61 54.77 750.91 819.14 854.30 890.66 968.51 8135 1
mu[60] 839.04 0.58 54.40 730.83 803.46 840.01 875.38 944.08 8700 1
mu[61] 840.22 0.58 54.53 730.86 804.92 839.83 877.18 945.32 8700 1
mu[62] 853.74 0.58 53.45 747.81 818.11 853.59 888.93 960.11 8481 1
mu[63] 865.24 0.61 54.24 761.70 828.65 863.97 900.32 974.94 7898 1
mu[64] 882.30 0.66 55.91 777.26 844.89 880.45 918.26 999.15 7255 1
mu[65] 887.76 0.68 57.26 781.16 848.54 885.70 924.93 1007.31 7016 1
mu[66] 875.24 0.63 54.80 771.44 838.01 873.95 910.92 988.55 7552 1
mu[67] 861.32 0.60 54.36 757.42 825.45 860.07 896.61 972.69 8202 1
mu[68] 856.11 0.60 54.96 748.91 819.66 855.56 891.69 967.17 8301 1
mu[69] 819.33 0.62 55.26 707.87 783.51 820.39 855.77 924.50 7997 1
mu[70] 791.53 0.76 59.05 669.34 753.64 793.97 832.11 902.11 5969 1
mu[71] 784.69 0.77 59.65 659.61 746.60 786.84 825.40 894.75 6023 1
mu[72] 803.98 0.66 55.41 691.57 767.86 804.88 842.32 908.76 7005 1
mu[73] 812.57 0.64 54.45 699.89 777.70 814.18 849.42 915.93 7187 1
mu[74] 818.27 0.62 54.40 708.10 782.44 819.20 855.95 923.24 7709 1
mu[75] 840.08 0.58 53.72 734.28 804.78 840.22 875.88 945.47 8497 1
mu[76] 869.03 0.67 55.81 764.41 831.60 866.65 904.90 984.00 6986 1
mu[77] 862.62 0.58 53.83 758.92 827.29 862.06 897.48 971.05 8700 1
mu[78] 860.49 0.58 54.17 755.43 823.74 860.09 896.44 969.63 8700 1
mu[79] 855.32 0.58 52.84 751.51 820.17 855.58 890.79 958.78 8177 1
mu[80] 852.45 0.58 53.92 745.01 816.83 853.03 888.00 957.59 8700 1
mu[81] 840.36 0.65 55.83 724.90 804.08 841.66 877.79 947.42 7367 1
mu[82] 846.36 0.67 55.62 731.18 810.81 848.29 883.83 951.42 6861 1
mu[83] 871.70 0.58 53.98 763.59 836.56 872.34 907.71 975.14 8700 1
mu[84] 904.03 0.67 55.36 799.31 867.03 903.52 939.68 1015.42 6770 1
mu[85] 908.13 0.65 55.45 803.24 871.25 907.13 943.28 1022.90 7276 1
mu[86] 910.75 0.61 54.06 807.03 873.88 909.71 946.27 1020.52 7935 1
mu[87] 898.71 0.58 53.90 793.32 862.57 898.81 934.32 1004.72 8700 1
mu[88] 907.56 0.58 53.26 803.83 871.83 906.85 942.74 1015.03 8435 1
mu[89] 914.95 0.63 53.90 811.79 879.40 914.14 949.84 1022.29 7310 1
mu[90] 910.37 0.58 54.18 802.16 875.49 910.03 945.65 1018.17 8629 1
mu[91] 925.41 0.65 55.07 818.95 888.23 923.70 961.15 1036.36 7151 1
mu[92] 922.12 0.66 55.72 816.87 884.40 919.94 958.22 1038.47 7135 1
mu[93] 924.15 0.70 57.14 815.47 885.69 922.37 960.39 1041.75 6585 1
mu[94] 933.22 0.82 61.00 820.67 891.52 930.06 972.13 1061.40 5543 1
mu[95] 895.59 0.66 55.00 789.60 858.62 894.74 931.35 1005.79 7002 1
mu[96] 855.16 0.60 55.57 744.96 818.13 855.66 892.09 963.32 8510 1
mu[97] 840.05 0.62 55.69 728.45 803.42 839.81 878.25 947.52 8100 1
mu[98] 805.98 0.74 60.62 681.42 765.89 807.54 846.73 921.59 6763 1
mu[99] 788.57 0.84 65.03 658.34 745.19 790.14 833.20 914.37 5943 1
mu[100] 783.83 0.96 72.93 637.40 735.97 785.78 833.96 922.56 5736 1
sigmaV 14655.31 47.77 3114.43 9149.18 12455.28 14436.28 16612.32 21271.22 4251 1
sigmaW 2831.26 38.42 1923.00 541.09 1455.94 2377.97 3689.42 7922.46 2506 1
lp__ -945.70 0.66 27.47 -992.55 -965.73 -948.12 -928.47 -885.48 1733 1
Samples were drawn using NUTS(diag_e) at Sun Dec 06 10:26:52 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
4.推定結果の取得と利用方法
せっかく状態が推定できたのですから、それを取り出したり図示したりしたくなります。
しかし、stan関数で得られた結果から直接中身を取り出すのは若干面倒です。
少々変則的ですが、いったんsummary関数を介してから結果を取り出すと楽でした。
まず、推定結果にsummary関数を直接適用するなら、以下のコードを実行します。
summary(Nile_LocalLevelModel_2)
この結果は、各chainごとの結果と3つのchainをまとめた結果が各々出力されます。
3つのchainをまとめた結果だけを抽出するには、以下のコードを実行します。
summary(Nile_LocalLevelModel_2)$summary
最初の6行だけ取り出してみます。
(右端が切れているときはコードの中で右スクロールしてください。隠れているだけで載っています。)
> # 計算結果をより細かく取得する
> # summary(Nile_LocalLevelModel_2)
> # summary(Nile_LocalLevelModel_2)$summary
> head(summary(Nile_LocalLevelModel_2)$summary)
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
muZero 1112.387 1.0024894 87.14434 943.3184 1054.260 1112.004 1167.669 1287.804 7556.468 1.0001447
mu[1] 1111.590 0.7796900 68.71982 980.2668 1065.453 1110.793 1156.835 1247.452 7768.195 1.0000220
mu[2] 1110.254 0.6516975 60.78630 992.6858 1069.503 1108.963 1150.491 1231.594 8700.000 0.9998428
mu[3] 1099.694 0.6223989 57.67308 986.6541 1060.690 1099.649 1138.505 1211.583 8586.351 0.9999688
mu[4] 1117.483 0.6390528 56.58290 1007.9916 1080.135 1116.662 1155.074 1231.142 7839.655 0.9997862
mu[5] 1115.749 0.6434993 55.67368 1008.9867 1078.793 1114.878 1152.251 1228.767 7485.206 0.9997759
ここまでくれば、例えば1列目のEAP推定量一覧を取り出すことは難しくありません。
やってみます。
> # EAP推定量一覧
> summary(Nile_LocalLevelModel_2)$summary[,1]
muZero mu[1] mu[2] mu[3] mu[4] mu[5] mu[6] mu[7]
1112.3872 1111.5898 1110.2543 1099.6937 1117.4830 1115.7489 1106.9830 1086.0044
mu[8] mu[9] mu[10] mu[11] mu[12] mu[13] mu[14] mu[15]
1121.8196 1136.3593 1105.7656 1070.1545 1048.7672 1050.2028 1037.3627 1033.3089
mu[16] mu[17] mu[18] mu[19] mu[20] mu[21] mu[22] mu[23]
1029.3824 1038.9289 1016.4136 1037.9143 1074.0917 1098.0986 1122.3501 1130.7681
mu[24] mu[25] mu[26] mu[27] mu[28] mu[29] mu[30] mu[31]
1139.2234 1129.7221 1099.4965 1047.4433 1002.8287 937.3674 904.5856 881.3580
mu[32] mu[33] mu[34] mu[35] mu[36] mu[37] mu[38] mu[39]
856.5047 863.3128 851.1026 840.0244 854.7951 853.4457 887.4731 896.2863
mu[40] mu[41] mu[42] mu[43] mu[44] mu[45] mu[46] mu[47]
874.9355 836.5543 798.2575 770.8792 805.3488 832.0178 886.8642 894.5858
mu[48] mu[49] mu[50] mu[51] mu[52] mu[53] mu[54] mu[55]
862.0727 838.8992 831.0844 823.9078 828.7638 830.2044 823.9159 809.6356
mu[56] mu[57] mu[58] mu[59] mu[60] mu[61] mu[62] mu[63]
817.2814 817.8134 833.0127 855.6544 839.0378 840.2202 853.7406 865.2420
mu[64] mu[65] mu[66] mu[67] mu[68] mu[69] mu[70] mu[71]
882.3016 887.7649 875.2397 861.3236 856.1085 819.3264 791.5320 784.6941
mu[72] mu[73] mu[74] mu[75] mu[76] mu[77] mu[78] mu[79]
803.9812 812.5720 818.2699 840.0789 869.0263 862.6233 860.4859 855.3247
mu[80] mu[81] mu[82] mu[83] mu[84] mu[85] mu[86] mu[87]
852.4549 840.3628 846.3607 871.7001 904.0288 908.1293 910.7539 898.7110
mu[88] mu[89] mu[90] mu[91] mu[92] mu[93] mu[94] mu[95]
907.5607 914.9454 910.3662 925.4120 922.1191 924.1495 933.2194 895.5865
mu[96] mu[97] mu[98] mu[99] mu[100] sigmaV sigmaW lp__
855.1568 840.0521 805.9837 788.5742 783.8264 14655.3143 2831.2560 -945.7024
>
鍵かっこを使う際は[行番号, 列番号]と指定すれば、ほしい結果だけ抽出できます。
「状態」であるmuだけを取り出しましょう。muは2行目から101行目までを占めていることに注意します。
(下のコードの2行目で指定しています)
> # muだけ取り出す
> summary(Nile_LocalLevelModel_2)$summary[2:101,1]
mu[1] mu[2] mu[3] mu[4] mu[5] mu[6] mu[7] mu[8]
1111.5898 1110.2543 1099.6937 1117.4830 1115.7489 1106.9830 1086.0044 1121.8196
mu[9] mu[10] mu[11] mu[12] mu[13] mu[14] mu[15] mu[16]
1136.3593 1105.7656 1070.1545 1048.7672 1050.2028 1037.3627 1033.3089 1029.3824
mu[17] mu[18] mu[19] mu[20] mu[21] mu[22] mu[23] mu[24]
1038.9289 1016.4136 1037.9143 1074.0917 1098.0986 1122.3501 1130.7681 1139.2234
mu[25] mu[26] mu[27] mu[28] mu[29] mu[30] mu[31] mu[32]
1129.7221 1099.4965 1047.4433 1002.8287 937.3674 904.5856 881.3580 856.5047
mu[33] mu[34] mu[35] mu[36] mu[37] mu[38] mu[39] mu[40]
863.3128 851.1026 840.0244 854.7951 853.4457 887.4731 896.2863 874.9355
mu[41] mu[42] mu[43] mu[44] mu[45] mu[46] mu[47] mu[48]
836.5543 798.2575 770.8792 805.3488 832.0178 886.8642 894.5858 862.0727
mu[49] mu[50] mu[51] mu[52] mu[53] mu[54] mu[55] mu[56]
838.8992 831.0844 823.9078 828.7638 830.2044 823.9159 809.6356 817.2814
mu[57] mu[58] mu[59] mu[60] mu[61] mu[62] mu[63] mu[64]
817.8134 833.0127 855.6544 839.0378 840.2202 853.7406 865.2420 882.3016
mu[65] mu[66] mu[67] mu[68] mu[69] mu[70] mu[71] mu[72]
887.7649 875.2397 861.3236 856.1085 819.3264 791.5320 784.6941 803.9812
mu[73] mu[74] mu[75] mu[76] mu[77] mu[78] mu[79] mu[80]
812.5720 818.2699 840.0789 869.0263 862.6233 860.4859 855.3247 852.4549
mu[81] mu[82] mu[83] mu[84] mu[85] mu[86] mu[87] mu[88]
840.3628 846.3607 871.7001 904.0288 908.1293 910.7539 898.7110 907.5607
mu[89] mu[90] mu[91] mu[92] mu[93] mu[94] mu[95] mu[96]
914.9454 910.3662 925.4120 922.1191 924.1495 933.2194 895.5865 855.1568
mu[97] mu[98] mu[99] mu[100]
840.0521 805.9837 788.5742 783.8264
EAP推定量と95%信用区間を取り出して保管します。
# EAP推定量と95%信用区間を取得 muEAP <- summary(Nile_LocalLevelModel_2)$summary[2:101,1] muLower95 <- summary(Nile_LocalLevelModel_2)$summary[2:101,4] muUpper95 <- summary(Nile_LocalLevelModel_2)$summary[2:101,8]
これで、推定結果の抽出ができました。
次は、図示してみましょう。
パラメタを見るだけだと結果がよく理解できません。推定結果はぜひ、実データと合わせて図示されることをお勧めします。これを見て「明らかにヘン」な結果になっているとすれば、モデルを修正することを検討します。
図示にはいろいろな方法がありますが、まずは、もともとのナイル川流量データと合わせて、推定値を時系列データに変換させるやり方を使ってみます。
# 時系列データ(ts)形式に修正 muEAP_ts <- ts(as.numeric(muEAP), start=1871, end=1970) muLower95_ts <- ts(as.numeric(muLower95), start=1871, end=1970) muUpper95_ts <- ts(as.numeric(muUpper95), start=1871, end=1970)
開始年や終了年はナイル川の流量データに合わせました。
後はplotするだけです。
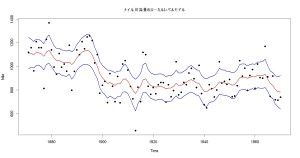
# プロット plot(Nile, type="p", pch=16, main="ナイル川流量のローカルレベルモデル") lines(muEAP_ts, col=2, lwd=2) lines(muLower95_ts, col=4, lwd=2) lines(muUpper95_ts, col=4, lwd=2)
パッと見問題なさそうです。
これで、ひとまず解析完了でしょうか。
お疲れ様でした。
おまけ1.ggplot2を使ったきれいなグラフを作る
おまけその1です。
さっきのやり方で図示はできるのですが、論文に出したり本に書いたりするにはちょっとカッコ悪い図ですね。
もっときれいなグラフを描くには「ggplot2」という外部パッケージを使うのが便利です。
まずはRを管理者として実行したうえで「install.packages(“ggplot2”)」を実行します。
これでパッケージをインストールした後で、以下を実行してください。
#-----------------------------------------------
# おまけ1.ggplot2を使ったきれいなグラフを作る
#-----------------------------------------------
# ggplot2を使ったもっときれいなグラフを作る
library("ggplot2")
これで準備完了。
きれいなグラフを作りましょう。
ggplot2を使う最初のステップは、「描画したいデータをまとめる」ことです。
描画にしか使わないので、雑な名前を付けておきました。
d1にはもともとのナイル川の流量データが、d2には、推定された「状態」が入っています。これは時系列データ形式ではなくデータフレーム形式(data.frame)にしておきます。
> # 描画したいデータをまとめる
> d1 <- data.frame(year=1871:1970, as.numeric(Nile))
> d2 <- data.frame(year=1871:1970, EAP=muEAP, lower=muLower95, upper=muUpper95)
> head(d1)
year as.numeric.Nile.
1 1871 1120
2 1872 1160
3 1873 963
4 1874 1210
5 1875 1160
6 1876 1160
> head(d2)
year EAP lower upper
mu[1] 1871 1111.590 980.2668 1247.452
mu[2] 1872 1110.254 992.6858 1231.594
mu[3] 1873 1099.694 986.6541 1211.583
mu[4] 1874 1117.483 1007.9916 1231.142
mu[5] 1875 1115.749 1008.9867 1228.767
mu[6] 1876 1106.983 997.7838 1215.568
次は描画する作業に移ります。
描画は、「グラフを重ねていく」イメージで作ります
NileGraphという名前でグラフ描画に必要な情報を格納します。
まずは、グラフの外側を作ります。
次に、さっき作ったNileGraphにデータ点を追加します。
# グラフの外枠の作成
NileGraph <- ggplot(
data=d1,
aes(
x=year,
y=Nile
)
)
# データ点を追加
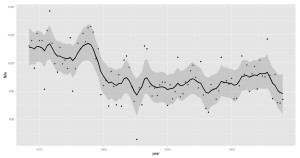
NileGraph <- NileGraph + geom_point()
11行目の「NileGraph <- NileGraph + ~~~」の部分が大事です。 2~8行目作ったグラフの情報NileGraphにさらに情報を追加していくのです。 今回はデータ点を付け加えるためにgeom_point()を足してやりました。 次に、Stanで推定された「状態」を追加します。
# EAP推定量と95%信用区間を追加
NileGraph <- NileGraph + geom_smooth(
aes(
ymin=lower, ymax=upper, y=EAP
),
lwd=1.2,
color=1,
data=d2,
stat=”identity”
)
「stat=”identity”」を指定しないと、勝手に別の方法で平滑化された結果がプロットされるので気を付けてください。
ほかはデータの指定や線の太さの指定(lwd=1.2)です。
グラフの情報を作ったので、これを描画します。
# 描画 plot(NileGraph)
きれいなグラフができました。
おまけ2.乱数の一覧を取得する方法
今まではsummaryの結果を使って、パラメタのEAP推定量や95%信用区間を求めていました。
しかし、シミュレーション結果はそのまま残っていますので、手作業で求めることも可能です。
まずは、シミュレーション結果の一覧を取得します。extract関数を使います。
#--------------------------------------- # おまけ2.乱数の一覧を取得する方法 #--------------------------------------- # 乱数の一覧を取得 resultMCMC <- extract(Nile_LocalLevelModel_2)
このシミュレーション結果は何個あるでしょうか。
例えば「左端」すなわち1870年の「状態」のシミュレーション結果の個数を出します。
> # シミュレーション結果は何個ある? > length(resultMCMC$muZero) [1] 8700
この8700が出る計算式はこちらです。
(1回のシミュレーション回数 - 捨てられたシミュレーションの個数)÷ 間引き数 × chain数
=((iter – warmup) /thin)*chain
ということで確認してみます。
> # ((iter - warmup) /thin)*chain > ((30000 - 1000)/10)*3 [1] 8700
8700個あるシミュレーション結果を使って平均値や95%区間を求めても、summary関数と同じ結果が出てきます。
> # シミュレーション結果の期待値をとると、EAP推定量が求まる
> mean(resultMCMC$mu[,1])
[1] 1111.59
> muEAP[1]
mu[1]
1111.59
>
> # 95%区間も同様
> quantile(resultMCMC$mu[,1], probs=c(0.025, 0.975))
2.5% 97.5%
980.2668 1247.4519
> muLower95[1]
mu[1]
980.2668
> muUpper95[1]
mu[1]
1247.452
おまけ3.結果の保存
最後に、解析手法とは関係ないのですが、実務に使う際に覚えておくとよいだろうことを書いておきます。
MCMCは計算に時間がかかります。
とても簡単なローカルレベルモデルでさえ数分かかります。
これがポアソン分布になりランダムエフェクトが入り、外生要因が入り、季節変動が入り……と複雑になっていくと、計算にものすごく時間がかかることになります。
その計算を何度も繰り返したくないですね。
というわけで、MCMCした結果は、確実に保存するようにしましょう。
そして、その推定結果を二次解析するというのが効率の良いやり方かと思います。
結果の保存は、Rのコンソール画面から行います。
エディタではなく、確実に「コンソール」すなわち、計算結果がずらずら表示される画面をクリックしてから行ってください。
コンソールをクリックしてから、上のほうにあるメニューの「ファイル」~「作業スペースの保存」を選択します。
例えば「localLevelModel.RData」という名前で保存します。
今回の計算例では大体20Mバイトありました。
次回以降は、いちいちstan関数を回さなくてもすぐに結果が手に入ります。
先ほど保存した「localLevelModel.RData」をダブルクリックして開きます。
そして、ライブラリの読み込みだけやっておきます。
# 作業スペースを読み込んだ後は、以下を実行するだけでOK library(rstan) library(ggplot2)
ちなみに、library関数とrequire関数は平文で使う場合は対して違いがないので、気にしないでください。
あとは、推定された結果をそのまま使うことができます。
# 推定されたパラメタ
Nile_LocalLevelModel_2
# 計算の過程を図示
traceplot(Nile_LocalLevelModel_2, pars=c("sigmaV", "sigmaW"))
# ggplot2による図示
plot(NileGraph)
stanを回すやり方と、二次解析のやり方を覚えておき、作業を分けられるようになればよいかと思います。
今回の記事では「4.推定結果の取得と利用方法」の章からが二次解析になります。
二次解析に関しては、実行に時間がかからないので、保存する必要はないでしょう。コードだけ残しておけば十分です。
参考文献
|
岩波データサイエンス Vol.1 特集「ベイズ推論とMCMCのフリーソフト」 何度も紹介している本ですね。 Stanを使って状態空間モデルを推定する方法が書かれています。 基礎を押さえた後は、こちらの本を読まれて、どんどん応用されていくのがよいかと思います。 |
|
状態空間時系列分析入門 状態空間モデルの基礎を押さえたい方にお勧めの本です。 一番簡単な状態空間モデルの入門書です。 |
リンク
この記事はベイズ推定を応用して状態空間モデルを推定する一連の記事の一つです。
記事の一覧とそのリンクは以下の通りです。
・ベイズ統計学基礎
・ベイズと統計モデルの関係
・ベイズとMCMCと統計モデルの関係
・Stanによるベイズ推定の基礎
・Stanで推定するローカルレベルモデル
スポンサードリンク




rstanを使う場合、データがNAを含む時はどういう対処をすればいいのでしょうか?