dlmの使い方
最終更新:2017年6月1日
Rのdlmパッケージを用いて、動的線形モデル(正規線形状態空間モデル)を推定する方法を書きます。
●状態空間モデル関連のページ
なぜ状態空間モデルを使うのか
状態空間モデル:状態空間モデルのことはじめ
dlmの使い方 :Rで正規線形状態空間モデルを当てはめる
ローカルレベルモデル:dlmパッケージを使ってローカルレベルモデルを当てはめる
季節とトレンド:dlmパッケージを使って季節成分とトレンドの入ったモデルを作る
dlmによる時変形数モデル:dlmによる「時間によって係数が変化する回帰モデル」の作成
Pythonによる状態空間モデル:R言語ではなくPythonを使いたい方はこちらをどうぞ
スポンサードリンク
目次
1.状態空間モデル推定の流れ
Step1 状態空間モデルの「型」を決める
Step2 パラメタを推定するー最尤法
Step3 カルマンフィルターする
Step4 スムージングする
2.実践dlm
1.状態空間モデル推定の流れ
状態空間モデルの細かい理屈は、実例を見せながら説明します。
そのまえに、どうやって状態空間モデルをRで推定するのかを説明します。
Step1 状態空間モデルの「型」を決める
Step2 その「型」にいれるパラメタを推定する
Step3 Step2で推定されたパラメタを「型」に入れてカルマンフィルターを回す
Step4 カルマンフィルターの結果を使ってスムージングする
Step4の「スムージング」はまだ説明してま せんが、下のほうで説明します。”予測”だけを目的とするならばなくてもいいかもしれませんが。
この流れは、dlmパッケージだけではなく KFASパッケージという状態空間モデルを推定できる別のパッケージを使っても、大体同じ流れになると思います。
Step1 状態空間モデルの「型」を決める
「型」というのは私の造語なのですが、その心はわかっていただけるのではないでしょうか。
状態空間モデルにはいろいろな「型」がありま す。
状態空間モデルが表す「状態」の変化のパタンがたくさんあるということです。また、「状態」から「観測値」へと変換されるプロセスにもいろいろなものが考えられます。まずはその「型」を決めるところから始まります。
「型」 は、対象に対してもともと持っていた知見を用いて決めていきます。たとえば、2000年に資源量が低位だったら、 2001年に突然高位になるということはたぶんないだろうなというのが経験上わかっていたとします。2001年にいったん中位になってから2002年くらいに高位になるだろうなと。こういう知識があると「資源量は一気には変化しない」けれども「緩やかな変化が続けば、かなり多い値にも低い値にも上下する」という状態の変化のパタンを設定してやればよいことになります。
この「型」が決まらなければ、ここから先には進めません。ここが最も頭を使うところなのかもしれませんね。
いろいろな「型」については実例を取り上げながら主に次のページ以降で説明します。
dlmパッケージだと、dlmModPoly( ) とか dlmModReg( ) とかいろいろな「型」が用意されているので簡単に「型」を設定することができます。また、これらの「型」はたとえば
dlmModPoly( ) + dlmModSeas( ) みたいに結合させることができます。
これはRならではのお手軽さですね。WinBUGS(ベイズ推定のためのソフト)では、こうはいきません。
型の一覧を書いておきます。今の段階でこれらの 型の意味を理解する必要はありません。
次のページから実例を挙げて順にみていきます。
dlmModPoly( )
order=1ならローカルレベルモデル(ランダムウォーク プラス ノイズモデル)
order=2ならローカル線形トレンドモデルを組むことができます。
dlmModReg( )
回帰分析のようにほかの説明変数の影響を加えられます。たとえば気温が高くなるとビールがよく売れるとかいうのを説明するために「気温」という説明変数を導入するとか。
dlmModSeas( )
季節変動を入れたモデルを組むことができます。
dlmModTrig( )
周期的な変動を入れたモデルを組むことができます。 dlmModSeasと違って三角関数(サインとかコサインとかいうやつら)をつかって周期的な変動を表します。
(2016年7月3日追記:関数の名称が間違っていたので修正しました)
dlmModARMA( )
状態空間モデルを使ってARMAモデルを推定することができます。
Step 2パラメタを推定する 最尤法
適当なパラメタを設定してやってdlmパッケージに突っ込んでやればものの1秒もかからずカルマンフィルターを使って状態空間モデルが推定できて しまいます。
そこで、その前段階にあたるパラメタの推定方法が、われわれエンドユーザー側として重要になる知識の一つなんじゃないかと思います。
パラメタの推定方法にはいろいろあるんですが、ここでは「最尤法」について説明します。
最尤法とは
パラメタA を使った時、「今手持ちのデータ」が再現できる確率は30%
パラメタB を使った時、「今手持ちのデータ」が再現できる確率は10%
であったときに、パラメタAを採用する、という考え方です。なぜならば、パラメタAのほうが「今手持ちのデータが再現できる確率」が高いからです。このように、「今手持ちのデータが再現できる確率」が最も高いパラメタを採用するのが最尤法です。
たとえば、コインを二回だけ投げて結果が「表・裏」だったとします。このコインの「表が出る確率」というパラメタは一体いくつが妥当だと思います か?
仮説1 パラメタは 1/3 だ!
仮説1を採用した時に「表・裏」という「今手持ちのデータ」が得られる確率は
1/3 × 2/3 = 2/9
仮説2 パラメタは 1/2 だ!
仮説1を採用した時に「表・裏」という「今手持ちのデータ」が得られる確率は
1/2 × 1/2 = 1/4
2/9 < 1/4 より、仮説2を採用した方が「今手持ちのデータ」が再現できる確率が高い
⇒仮説2「表が出る確率は1/2」を採用する
という流れが最尤法です。
暇な人は調べてみるといいと思いますが、この場合「今手持ちのデータが再現できる確率」が最も高くなるのはパラメタが1/2のときになります(微分使えば解けます)。
このように「今手持ちのデータが再現できる確率」が最も高いパラメタが最も尤もらしい(「もっともらしい」と読みます)と考えて、そいつを採用するのが最尤法です。
「今手持ちのデータが再現できる確率」のことを「尤度(ゆうど)」といいます。計算の簡単のため対数を取った対数尤度を使うことが多いです。
今までの話は、対数尤度が最も高くなる「最大化対数尤度」を得ることができるパラメタを推定する、とカッコよく言い直すとこうなります。
ここら辺の話は、北大水産で行った統計勉強会のスライドを読むとより理解が深まると思います。とくに2 2.尤度と最尤法や2 3.GLMの基礎あたりが最尤法の解説ですね。
状態空間モデルにこれを適応します。
まず「テキトーな」パラメタをつかってカルマンフィルターをしてやり状態空間モデルを推定します。
そしてそのときの「今手持ちのデータが再現できる確率(尤度)」を計算してやります。
その「今手持ちのデータが再現できる確率(尤度)」が最も高くなるようにパラメタを変更してやって、最も尤もらしいパラメタを見つけます。
そして、またそのパラメタを使って状態空間モデルを推定しなおしてやれば、最も尤もらしい状態空間モデルが出来上がります。
dlmMLE( ) という関数を使えば簡単に最尤法が適用できます。
じつはこの関数は有名な最適化関数optim( )をそのまま使っています。なのでoptimで使われる匠の技(?)的なパラメタ推定方法がそのまま使えます。技術的な話は実例を挙げながら次のページで 説明します。
Step 3 カルマンフィルターする
dlmFilter( 使うデータ, モデルの型 ) で簡単にカルマンフィルターができます。
計算するだけなら一瞬です。
Step 4 スムージングする
そもそも「スムージング」とはなにか、まだ説明していなかったのでここに書きます。
まず、2000年のデータから2001年状態を予測して、そして予測された状態を、2001年の観測値をもとにして補正しました。このように補正 するのがフィルタリングでした。前のページに書いた内容ですね。
一方のスムージングは、2002年、2003、2004年の観測値を使って2001年の補正をします。
別に3年あととかはどうでもよくって、「将来の値をもとにして過去の状態を補正する」のがスムージングの心です。
将来の値なんてわからないんだからやったって無駄じゃんと思うかもしれませんが、今手持ちのデータすべてを使って過去を説明できるんですから、知識発見 という意味合いでは便利です。
dlmSmooth(フィルタリングしたやつ) で簡単に計算できます。これも1行ですね。
2.実践 dlm
dlmしてみます。
細かい話は次のページ以降で説明するとして、まずはモデルを推定する流れをつかんでもらう程度の中身にします。
すべてまとめたスクリプトはこちらにおいておきます。これはPetris and Petron (2011)を一部改訂したものです。
まず、Nileというデータを使うことにします。これはRにデフォルトで入ってるデータです。
> Nile
Time Series:
Start = 1871
End = 1970
Frequency = 1
[1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994 1020
[16] 960 1180 799 958 1140 1100 1210 1150 1250 1260 1220 1030 1100 774 840
[31] 874 694 940 833 701 916 692 1020 1050 969 831 726 456 824 702
[46] 1120 1100 832 764 821 768 845 864 862 698 845 744 796 1040 759
[61] 781 865 845 944 984 897 822 1010 771 676 649 846 812 742 801
[76] 1040 860 874 848 890 744 749 838 1050 918 986 797 923 975 815
[91] 1020 906 901 1170 912 746 919 718 714 740
1871年から1970年までのナイル川の流量データです。ちょうど100年間分のデータです。
plot(Nile, type=”o”,col=8)
Step1から順番にモデルを推定していきます。
# Step1 モデルの型を決める
build.1 <- function(theta){
dlmModPoly(order=1, dV=exp(theta[1]), dW=exp(theta[2]))
}
今回は dlmModPoly(order=1)ということで、ローカルレベルモデル を推定します。ローカルレベルモデルとは何者かということは次のページで説明します。とりあえず簡単なモデルです。
ここで function(theta)とかいう変なものがついています が、これは自分で関数を作るということを表しています。thetaというパラメタを入れるとdlmModPoly関数を使って独りでにモデルを作ってくれるという関数を作ったんですね。
こういう風にいったん型を関数にまとめてしまってからパラメタ推定に移ります。optim関数を知っている人はすんなり納得しやすいような気はします。知らない方も覚えておきましょう。自作関数をfunction()で作る~optim系の関数で最適化という流れはよく出てきます。
今回推定するのは、二つの分散です。一つは観測誤差の大きさ。もう一つは状態そのものが変動するその大きさです。こうやって「状態そのものが変動している」のと「観測誤差が入っている」という両方の変動を加味してモデルを組みます。exp()が ついているのは、分散の大きさが絶対正の値になるからその指定のためです。expとは指数ですね。eの何とか乗という値は決して負になりません。
では、最適化のための準備が整ったので最尤法でパラメタを推定しましょう。
# Step2 パラメタ推定
fit.1 <- dlmMLE(Nile, parm=c(1, 1), build.1)
結果はこちら
> fit.1
$par
[1] 9.622439 7.291970$value
[1] 549.6918$counts
function gradient
29 29$convergence
[1] 0$message
[1] “CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH”
これは実質1行で計算できるので楽ですね。dlmMLE(Nile, parm=c(1, 1), build.1)を してやるだけです。推定するパラメタが二つあるのでparm=c(1,1)という風に二つ初期値をテキトーに入れてやると勝手に計算してくれます。
推定されたパラメタを使ってモデルを組みなおします。太字は私が勝手に入れました。
# 推定された分散を使って、モデルを組みなおす
mod.Nile <- build.1(fit.1$par)
結果はこちら
> mod.Nile
$FF
[,1]
[1,] 1$V
[,1]
[1,] 15099.84$GG
[,1]
[1,] 1$W
[,1]
[1,] 1468.461$m0
[1] 0$C0
[,1]
[1,] 1e+07
なんだか怪しげなパラメタがたくさん出てきましたが、FFとかGGとかいうのは”推定されたパラメタ”ではありません。モデルの「型」を作るための構成要素です。今回は説明しませんが、じつはdlmModなんとかっていう関数を使わなくても、このFFだのGGだのを指定してやれば自分で何でも自由にモデルを組むことができます。行列の掛け算とかがわかる方は、参考文献の数式を見るとFFやGGの意味がすぐ分かると思います。今回は省略します。
とりあえず今回大事なのは VとW です。Vは観測誤差の大きさ(分散)を表していて、Wは状態の変動の大きさ(プロセスエラーの分散)です。 Wより Vのほうが大きくて、観測誤差のほうが大きいということがわかります。
ちなみに$マークの意味は大丈夫ですよね。$は入れ子構造になったリストのことで、「結果$中身」とすれば、結果の中から必要な中身だけ抽出できます。
ではではフィルタリングをしましょう。
# Step3 フィルタリング
NileFilt <- dlmFilter(Nile, mod.Nile)
ここまで来ると後は楽です。一行でカルマンフィルターが完了して、モデルが出来上がりました
dlmFilterにデータであるNileと出来上がったモデルの型mod.Nileを入れれば完成。
Step2までの作業はモデルの「型に入れるパラメタ」を決めるための作業だったんですね。「型」が決まれば、フィルタリングは秒で終わります。
# Step4 スムージング
NileSmooth <- dlmSmooth(NileFilt) # スムージングする
スムージングも一行で完了。dlmSmoothにフィルタリングした結果であるところのNileFiltを入れればできます。
結果
中身は示しませんが、推定された「状態」を表示させるには以下を実行すればよいです。
NileFilt$m # カルマンフィルターで推定された状態
NileSmooth$s # スムージングされた結果
$マークを使って一部だけを抽出しました。これをしないとびっくりするくらいたくさんの結果が出てきてしまって何が何だか分からなくなってしまいます。
結果をプロットします。まずはカルマンフィルターの結果です。dropFirstと は一番最初の値を取り除く処理です。なぜこれが必要なのかを説明するとまた1章分くらい文章を消費しちゃうので後回しにします。次のページ(ローカルレベルモデル)で解説するのでお楽しみに
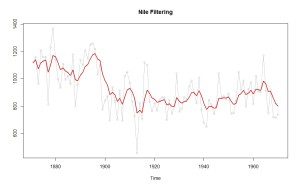
plot(Nile, type=”o”, col=8, ylab=””, main=”Nile Filtering”)
lines(dropFirst(NileFilt$m), col=2, lwd=2)
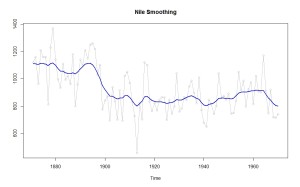
次はスムージングした結果です。こっちのほうが滑らかになってますね。
plot(Nile, type=”o”, col=8, ylab=””, main=”Nile Smoothing”)
lines(dropFirst(NileSmooth$s), col=4, lwd=2)
ここで引っ張った線はナイル川の流量の見えない「状態」を表しています。毎年よくわからない観測誤差が入ったモノを私たちは観測しているんだけれ ども、その見えない流量の水準はいったいいくらかというのを推定したら赤い線とか青い線とかになるわけです。
で、1920年の流量の見えない「状態」を1920年までの観測結果から推定したのが赤い線(フィルタリングの結果)で、手持ちの100年間のデー タすべてをフルに使って状態を推定したのが青い線(スムージング)の結果となります。
これでとりあえず状態空間モデルを一通り回すという作業ができたことになります。
とはいえ(確信犯的に)状態空間モデルの「型」の理屈をすっ飛ばしていますので、もやもやした感じが残っているのではないでしょうか。
次のページからはこの状態空間モデルの内容をもうちょっと掘り下げていきます。
ローカルレベルモデル dlmパッケージを使ってローカルレベルモデルを当てはめる
季節とトレンド dlmパッケージを使って季節成分とトレンドの入ったモデルを作る
dlmによる時変形数モデル dlmによる「時間によって係数が変化する回帰モデル」の作成
バグや誤り等ございましたら、メールなどでご一報頂けると大変ありがたいです。
参考文献
|
|
 |
|
Rによるベイジアン動的線形モデル (統計ライブラリー) Dynamic Linear Models with Rの日本語訳です。 |
 |
|
状態空間時系列分析入門 このサイトでいつも紹介している、状態空間モデルの入門書です。 状態空間モデルについて知りたければ、まずはこの本から始めるのが良いと思います。最も読みやすい状態空間モデルの入門書です。 |
 |
書籍以外の参考文献
・Giovanni Petris (2010), An R Package for Dynamic Linear Models. Journal of Statistical Software, 36(12), 1-16.
英語ですが、無料で読めるdlmの解説文です。
状態空間モデル関連のほかの記事が読みたい方はこちらをどうぞ
スポンサードリンク


現在状態空間モデルを勉強しているため、よくブログ拝見しています。
細い指摘で申しわけありませんが、モデルの型を決める、の部分で関数名に
誤りがあったので連絡させていただきました。周期性を持った状態空間モデルを
試そうとした時に気付きました。
dlmModtrig( ) -> dlmModTrig()
これからも頑張ってください。失礼いたしました。
Masa.S様
コメントありがとうございます。
管理人の馬場です。
上記の件、確かに間違っていました。
修正しておきました。
ご指摘ありがとうございます。
今後はミスの無いように、注意していくつもりですが、
また何かあればご指摘いただければ幸いです。
以上です。
正規線形状態空間モデル とは何の訳語なのでしょうか? normal linear state space modelでしょうか?
ぼたもち様
コメントありがとうございます。
管理人の馬場です。
gaussian linear state space modelの略ですね。
linear gaussian state space modelと書かれることもあるようです。
スムージングとは
「2002年、2003、2004年の観測値を使って2001年の補正をします。」
とのことですが、dlmSmoothという関数ですが
どのようなアルゴリズを使っているのでしょうか?
ライブラリを登録しないと使えないのでしょうか?
宜しくお願いします
PS:
その他の情報は色々と詳しく掲載されているので
大変参考にさせていただいています
コメントありがとうございます。
管理人の馬場です。
ローカルレベルモデルにおける、平滑化の方法は、拙著「時系列分析と状態空間モデルの基礎」の第5部第7章に記載しています。
興味があれば参照してください。
https://logics-of-blue.com/tsa-ssm-book-support/
コードだけでよければ、Web上でも公開しています。
https://github.com/logics-of-blue/book-tsa-ssm-foundation/blob/master/book-data/5-7-実装:Rによる状態空間モデル.R
早速の返信をいただきありがとうございました
「時系列分析と状態空間モデルの基礎」を読ませていただきます
本を読んで分かりました
ありがとうございました
追加質問です
mu_smoothはデータのスムージング結果ですが
P_smoothの意味は何でしょうか、活用方法は何でしょうか?
拙著をお読みいただきありがとうございます。
> P_smoothの意味は何でしょうか
状態の予測誤差の分散です。
> 活用方法は何でしょうか?
分散ですので、例えば推定された状態の95%信頼区間を計算する際などに利用できます。
> 活用方法は何でしょうか?
分散ですので、例えば推定された状態の95%信頼区間を計算する際などに利用できます。
とのことですが、95%信頼区間を計算する方法を教えていただけないでしょうか
宜しくお願い致します。