季節とトレンド
最終更新:2017年6月1日
dlmパッケージを使って、ちょっと複雑な正規線形状態空間モデル(動的線形モデル)を推定します。
今回は、トレンド成分と季節成分の入った状態空間モデルを推定し、予測を行うところまでを行います。
●状態空間モデル関連のページ
なぜ状態空間モデルを使うのか
状態空間モデル:状態空間モデルのことはじめ
dlmの使い方 :Rで正規線形状態空間モデルを当てはめる
ローカルレベルモデル:dlmパッケージを使ってローカルレベルモデルを当てはめる
季節とトレンド:dlmパッケージを使って季節成分とトレンドの入ったモデルを作る
dlmによる時変形数モデル:dlmによる「時間によって係数が変化する回帰モデル」の作成
Pythonによる状態空間モデル:R言語ではなくPythonを使いたい方はこちらをどうぞ
スポンサードリンク
目次
1.ローカルレベルモデルを発展させる
2.トレンド
3.ローカル線形トレンドモデル
4.季節成分
5.dlmで季節とトレンド
6.dlmな予測
1.ローカルレベルモデルを発展させる
こちらで書いたように、一番単純な動的線形モデルであるローカルレベルモデルはデータから正しそうな状態を推定するということはある程度可能でしたが、予測には何の役にも立ちませんでした。
これは、モデルを作るのに使った「データに対する知識」があまりにも少なかったことが原因です。
たとえば、「このデータは上昇(下降)トレンドがある」とか、「毎年8月には高い値を示す」といった季節変動といったの知識を取り込むとより良い予測が可能です。
というわけで、今回は、その 「トレンド」 と 「季節」 に焦点を当てて、これらの要因を動的線形モデルに付け加える方法について記します。
2.トレンド
トレンドは大きく分けて2つあります。
一つは、確定的トレンド
もう一つが確率的トレンド
です。
確定的トレンドは、回帰分析を思い出してもらえるとよいです。散布図に直線を引っ張るアレです。
横軸に時間を取って、縦軸にたとえばビールの売り上げを置いたら、それこそ右肩上がりに一定のスピードで増加していく、というのが確定的トレンド。
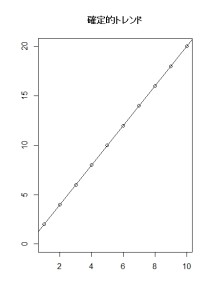
図で示すとこんな感じです。
上のグラフの場合は、時間が1増えるごとに、ビールの売り上げは2ずつ増えていっていることがわかると思います。
一定して、時間が1増えると、売り上げが2増える、というのが、確定的トレンドです。
一方、確率的トレンドは、その名の通り、確率的に増加(減少)分が変化します。
この変化のパターンもランダムウォークです。
一期前のトレンドと似たようなトレンドになるけれども、ちょっと値が変わるということです。
3.ローカル線形トレンドモデル
トレンドとローカルレベルモデルを合体させたもののイメージをつかんでいただくために、例を使って説明します。
2000年におけるビールの売り上げは10本。その時のトレンドは、+4でした。
順当にいけば2001年は14本売れることになります。
最尤法をした結果、観測誤差は±7の範囲を持つことがわかり、状態の変動の大きさは±4であることが推定できたとします。さらに、トレンドの変動の大きさは±2でした。
2000年の状態は10でした。
2001年は、10から±4の範囲内で動く可能性があります。さらに、トレンドは4±2なので、2~6の範囲で変動します。
サイコロを振ったら状態の変化は+3になったとします。さらに、トレンドの変化は-2になったとします。
すると、2001年の状態は
10(元の値) + 3(状態の変動) + 4-2(トレンド) = 15 となります。
ノイズの大きさは常に±7なので、2001年の観測値は、8~22の範囲内に収まるだろうと考えられます。
予測を行う際、サイコロは正負どちらに転ぶかわかりません。そういう時は「変化しない」を前提として予測するんでした。ですから、2001年の予 測値は
10(2000年の状態の値) + 0 + 4(2000年のトレンドの値) = 14
という風に予測されます。で、2001年のデータが手に入ったら、それをもとにして予測された状態を補正する、という流れは一緒です。
4.季節成分
今度は季節成分について説明します。
季節成分の入れ方には三角関数(サインとかコサインとか)を使ったやり方と、ダミー変数を使ったやり方の2種類がありますが、ここでは後者のダミー変数を使う方法だけを説明します(dlmパッケージを使って三角関数な季節成分を推定することも可能です)。
ダミー変数を使ったやり方とは、単純にひと月ごとに売り上げの大きさの補正をすることです。1月にはビールは売れないけど、8月にはよく売れる、といったような感じ。
この季節成分にもシステムノイズを入れ込むことは可能です。ノイズがあるのが確率的季節成分、ないのが確定的季節です。
たとえば、1月には売れ行きが悪くて-5の補正、2月には若干ましになって-3の補正を受けたとします。
2000年1月の売り上げは10でした。季節成分だけを見ると、2月は1月よりプラス2になっているので、2000年2月の売り上げは12となるはずです。これがシステムノイズがない場合。
システムノイズがあるときは、ローカルレベルモデルなんかと同じく、季節ごとにさいころを投げてやります。季節には±1の変動があったとしたら、 2000年2月の値は、11~13ということになります。
もちろんこの季節のブレだけでなく、ローカルレベルモデルで表された状態の変動やトレンドの変動なんかも加えていくことが可能です。
5.dlmで季節とトレンド
今回使ったソースはこちらにおいてあります。
今回は、季節成分とトレンド両方がありそうなデータとして、AirPassengersというデータを使います。
もともとのデータを対数変換したものを解析の対象として使います。
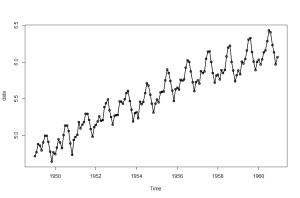
data <- log(AirPassengers)
plot(data, type=”o”, lwd=2)
まずは、状態の変化に一切確率的な変動がない、プロセスノイズが全部0なモデルを推定します。
ローカルレベルモデルで示したよう、システムノイズが0な状態空間モデルは、普通の線形回帰をした場合と一緒の結果になります。ですので、このモデルは重回帰分析を使うことによっても推定可能です。暇な方は試してみてください。
dlmパッケージを落としてから
library(dlm)
あとは、以前に示したように4ステップで推定完成です。
# レベルも傾きも、季節変動も、システムノイズ0 観測誤差のみ
# Step1
# モデル作成のための関数を作る
build.4 <- function(theta){
dlmModPoly(order=2,dV=exp(theta[1]),dW=c(0,0))+
dlmModSeas(fr=12,dW=c(0,rep(0,10)),dV=0)
}# Step2
# MLEでパラメタ推定。
fit.4 <- dlmMLE(
data,
parm=dlmMLE(data,parm=c(1),build.4,method=”Nelder-Mead”)$par,
build.4,
method=”BFGS”
)# 推定されたパラメタを使ってモデルを作り直す
DLM.4 <- build.4(fit.4$par)# Step3
# カルマンフィルター
Filt.4 <- dlmFilter(data, DLM.4)# Step4
# スムージング
Smooth.4 <- dlmSmooth(Filt.4)
モデルの型を決める作業が一番大きく変わったと思います。
build.4 <- function(theta){
dlmModPoly(order=2, dV=exp(theta[1]), dW=c(0,0)) +
dlmModSeas(fr=12, dW=c(0,rep(0,10)), dV=0)
}
において、緑の部分がローカル線形トレンドモデル(ローカルレベルモデル+トレンド)で、紫が季節の成分です。両者を + でつなげば簡単に合体できます。
緑の部分から説明します。太線になっているorder=2ですが、これが1ならば単なるローカルレベルモデルで、2にするとトレンド付きになります。ちなみにデフォルトは2なので、いちいち書かなくても実は問題ありません。
dVは観測誤差で、この大きさは推定しています。でも、状態そのものは確率的に変動しないというモデルを今回は組んでいるので、dWは0を指定しています。ここで、dWに二つも0を入れていますが、一つ目はローカルレベルモデルで説明した状態の変動の大きさを表し、二つ目はトレンドの変動の大きさを指定しています。ですので、片方だけ0とか言ったモデルももちろん推定できます。
紫の部分は季節を表したところですが、これにはdlmModSeas()を使います。fr=12とは、一年の間に12こデータがありますよという 指示。たとえば春夏秋冬4つの区分しかなければfr=4とします。
dWにやけにたくさん0があります(最初の0に追加してrep()でさらに0を10個生産している)が、これは最後の10個の0はほぼ確定です。気にせ ず0を入れればよいです。
dWの一番最初の値はまた別です。季節が確率的変動をする場合は、この大きさも推定することになります。逆に言えば、季節が確率的変動をしない場合でも、最後の0を10個くっつけるところは変化しないことに気を付けてください。
観測誤差のほうはdlmModPoly()で推定されているので、ここには0を突っ込んでおきます。
推定された観測誤差は
> DLM.4$V
[,1]
[1,] 0.0035172
となりました。ふつうにDLM.4と推定されたモデルの型を表示させるとすごくたくさんの数値が出てきますが、基本的な見方はローカルレベルモデルと一緒なので省略します。季節があるから、その分表示する量が多くなったんですね。
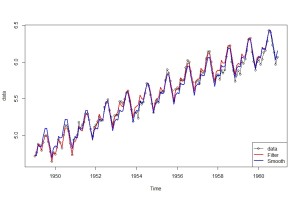
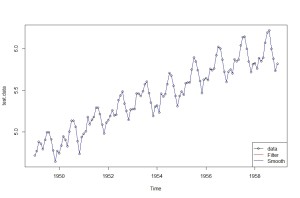
グラフを書きます
plot(data, col=1, type=”o”, lwd=1)
lines(dropFirst(Filt.4$m)[, 1] + dropFirst(Filt.4$m)[, 3], col=2, lwd=2)
lines(dropFirst(Smooth.4$s)[, 1] + dropFirst(Smooth.4$s)[, 3], col=4, lwd=2)legend(“bottomright”, pch=c(1,NA,NA),
col=c(1,2,4), lwd=c(1,2,2), legend=c(“data”,”Filter”,”Smooth”))
lines(dropFirst(Filt.4$m)[, 1] + dropFirst(Filt.4$m)[, 3], col=2, lwd=2)のように、推定された状態の値の1列目と3列目を足し合わせた値を表示させています。
じっさいのところ、推定されたFilt.4$mには13列のデータがあります。そ のうち、「最終結果」にはどの列を使えばよいのかということは、モデルのFを見ればわかります。
> DLM.4$F
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
1 0 1 0 0 0 0 0 0 0 0 0 0
これで、1列目と3列目だけが1になっているのがわかると思います。このFが何なのかを説明するには行列の掛け算の式を出さないといけない(実はかなり簡単です。でも、このサイトでは行列を載せにくい)ので省略しますが、とりあえずこれを見れば何を使えばよいかがわかります。
ちなみに、1列目はローカルレベル+トレンドの値、2列目はトレンドの値、3列目はその時期における季節成分です。だから1,3列目だけで十分だった と。
4列目以降はその時期以外の季節成分たちです。補欠みたいなものですね(?)
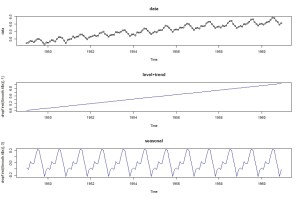
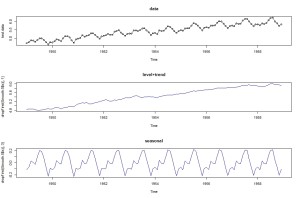
季節とかトレンドとかを別々のモデルで推定したので、結果も別々に表示させることができます。たとえばスムージングされた結果を使えば。
par(mfrow=c(3, 1))
# 元データ
plot(data, col=1, type=”o”, main=”data”)
# レベル+トレンド成分
plot(dropFirst(Smooth.4$s)[, 1], col=4, main=”level+trend”)
#季節成分
plot(dropFirst(Smooth.4$s)[, 3], col=4, main=”seasonal”)
par(mfrow=c(1, 1))
これを見れば、右肩上がりのトレンドがあること、そして、季節的な変動パタンが一目でわかります。
6.dlmな予測
次は予測をやってみます。1959年以降を切り落として、2年先までを予測することにします。
今度はシステムノイズも全部推定したモデルを作ります。
「全部」とは、ローカルレベルで説明した状態の変動と、トレンドの変動と、季節成分の変動です。
今回は推定すべきパラメタが多いので、計算には多少の時間がかかります。また、最適化には多段階最適化法を使っていますが、それでも初期値の感度が大きくて、値を変えると別の結果が出たり、永遠に計算が終わらなかったりすることもあります。あくまでも暫定的な結果ということで見てください。
# 1959年以降を切り落とす
test.data <- window(data,end=c(1958, 12))# Step1
# モデル作成のための関数を作る
build.5<-function(theta){
dlmModPoly(order=2,dV=exp(theta[1]), dW=c(exp(theta[2]), exp(theta[3])) ) +
dlmModSeas(fr=12, dW=c(theta[4], rep(0,10)), dV=0)
}# Step2
# MLEでパラメタ推定。
fit.5 <- dlmMLE(
test.data,
parm=dlmMLE(test.data,parm=c(0,1,1,1),build.5,method=”Nelder-Mead”)$par,
build.5,
method=”BFGS”
)# 推定されたパラメタを使ってモデルを作り直す
DLM.5 <- build.5(fit.5$par)# Step3
# カルマンフィルター
Filt.5 <- dlmFilter(test.data, DLM.5)# Step4
# スムージング
Smooth.5 <- dlmSmooth(Filt.5)
なぜかフィルタリングの結果とスムージングの結果がほとんど一緒(わずかに違う値でした)でしたが、とりえあず気にしないで先に進んでいきます。
今回も、前に作った確定的なモデルと同じようにトレンドと季節に分けて表示させてやります。
par(mfrow=c(3,1))
# 元データ
plot(test.data,col=1,type=”o”, main=”data”)
# レベル+トレンド成分
plot(dropFirst(Smooth.5$s)[,1],col=4, main=”level+trend”)
# 季節成分
plot(dropFirst(Smooth.5$s)[,3],col=4, main=”seasonal”)
par(mfrow=c(1,1))
トレンドも季節もちょっとぶれてることがわかると思います。真ん中のトレンドのグラフは、季節調整済みデータとして使うこともできるでしょう。
で、次は本命の予測です。
dlmForecast()関数を使えば割と簡単に計算できます。
# 予測
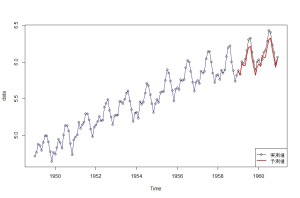
Fore <- dlmForecast(Filt.5, nAhead=24, sampleNew=5)# 予測の答え合わせ
plot(data, type=”o”)
lines(dropFirst(Smooth.5$s)[,1]+dropFirst(Smooth.5$s)[,3],col=4)
lines(Fore$f,col=2,lwd=2)legend(
“bottomright”,pch=c(1,NA),col=c(1,2),lwd=c(1,2),legend=c(“実測値”,”予測値”)
)
ちょっと過小評価してますが、まぁまぁあっていそうです。
ここで、dlmForecast(Filt.5,nAhead=24,sampleNew=5)と書きましたが、nAhead=24で予測する期間を設定します。あとのsampleNew=5は、 予測値から乱数を使って出された予測値です。何のことかというと、予測値はあくまでも「予測された状態」です。なので、これに観測誤差なんかが加わって観測値が出てくることになります。ということは、実際に観測値が出るとしたらどんな値が出るのか気になりますよね。それをシミュレーションしたんです。
表示させてみます。
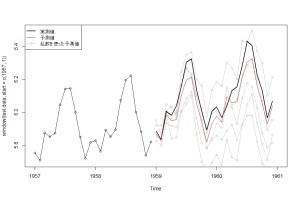
# 乱数を使って予測
Line <- function(x){
lines(x, col=8, type=”o”)
}plot(window(test.data,start=c(1957,1)), xlim=c(1957,1961), ylim=c(5.7,6.5), type=”o”)
lapply(Fore$newObs, Line)
lines(window(data,start=c(1959,1)), col=1,lwd=2)
lines(Fore$f, col=2)
legend(“topleft”, pch=c(NA,NA,1), col=c(1,2,8), lwd=c(2,1,1), legend=c(“実測値”,”予測値”,”乱数を使った予測値”))
これをみると、予測結果からあり得なさそうな実測値が得られたわけではなさそうだということがわかります。これを使うと確率予報なんかも簡単にでき ますね。シミュレーション結果を100個作って、そのうちの20個が100を超えたら、「100を超える確率は20%です」と予測してやればよいわけで す。近似的な確率ですが、予測の幅が広がります。
バグや誤り等ございましたら、メールなどでご一報いただけると幸いです。
参考文献
|
Dynamic Linear Models with R (Use R!) 私がdlm関連の記事を書くときは、いつもこの本を参考にしています。 dlmパッケージを使いこなしたい方はぜひどうぞ。 |
|
Rによるベイジアン動的線形モデル (統計ライブラリー) Dynamic Linear Models with Rの日本語訳です。 |
 |
|
状態空間時系列分析入門 このサイトでいつも紹介している、状態空間モデルの入門書です。 状態空間モデルについて知りたければ、まずはこの本から始めるのが良いと思います。最も読みやすい状態空間モデルの入門書です。 |
 |
状態空間モデル関連のほかの記事はこちらから見ることができます
スポンサードリンク



たびたびすみません。東京の大学で勉強をしている学生です。本稿においてトレンドと季節に分けて表示する場合、フィルタの結果にするとトレンドと季節の最初のほうの値がかなり不安定になるのを見つけました。この原因がわかれば、シェアさせていただきたいです。
haoさん
こんばんは。
管理人の馬場です。
ご質問ありがとうございます。
不安定というのは、パラメタの影響を強く受けるということでしょうか。
「推定されたパラメタの値が変わることによって状態の推定結果が大きく変わる」という現象かなと想像して、以下、回答いたします。
結果が不安定になるのは、仕方がないところもあります。
まず、フィルタリングとは「今まで手に入ったデータをもとに」状態を推定する行為です。
2000年1月からスタートして毎月データを取得したとします。
2000年2月時点では、データが2つしかありません。このデータだけで状態を推定します。
2000年3月時点では、3つだけのデータで状態を推定します。
そのため、季節モデルに限らず、フィルタリングの初期(時系列的に古い)の値は不安定になりやすいです。
例えば、ローカルレベルモデルにおいて、左端(dlmパッケージにおける「m0」の値)を0にするか、1000にするかで、もっとも古い時間の状態推定値は1000もの開きがあることになります。パラメタの影響をもろに受けるんですね。
しかし、データが増えることによって、この開きは少なくなります。
というわけで、フィルタリングした結果において、初期の状態推定値が安定しない(パラメタの影響を強く受ける)ことは、仕方ないことです。
季節モデルはローカルレベルモデルに比べて少々複雑なモデルなので、この影響が強く出たのかもしれません。
これがまずければ、スムージングを検討されてみてください。スムージングですと、全てのデータを使うので、比較的安定すると思います。
はじめまして。ただいま状態空間モデルに挑戦中のものです。
正直このページが一番親切で役立っております。
一つ質問なのですが、順々に実行していくとstep2でエラーが出ます。
# Step2
# MLEでパラメタ推定。
fit.5 <- dlmMLE(tm,parm=dlmMLE(tm,parm=c(0,1,1,1),build.5,method="Nelder-Mead")$par,build.5,method="BFGS")
の部分ですが、test.dataの部分を自分のデータtm # Step2
Browse[1]> # MLEでパラメタ推定。
Browse[1]> fit.5 <- dlmMLE(tm,parm=dlmMLE(tm,parm=c(0,1,1,1),build.5,method="Nelder-Mead")$par,build.5,method="BFGS")
Error during wrapup: Inconsistent dimensions of arguments
たなっぺ様
こんにちは。
管理人の馬場です。
当サイトをご利用いただき、ありがとうございます。
こちらで確認をしたところ、やはりStep2が動かないことを確認しました。
これは、ダブルクォーテーションマークが全角になっているため、エラーで落ちてしまっていたようです。
上記の事例は、過去にほかのページでも見られておりました。修正したつもりでしたが、申し訳ありません。
今回は、Wordpressの設定ごと変更をいたしました。
現在は、ダブルクォーテーションマークは半角のまま表示されているので、コピペされても動くかと思います。
よろしくお願いします。
一部訂正前のものを送ってしまったので訂正です。
自分のデータtm<-hoge$hogeに変えてやってみたのですが、エラーが出て通りません。
次元があっていないとの次元があっていないとのことですが、どこが原因なのでしょうか。おわかりでしたら時間のあるときでも良いのでよろしくお願い致します。
はじめまして。
いつもこちらのサイトで勉強させてもらっております。
ひとつ些細なことをお伺いしたいのですが、
ローカルレベルモデルに季節成分を入れる方法である、
三角関数を用いる場合と、
ダミー変数を用いる場合とでは、
どちらがより一般的なのでしょうか。
Naoki様
初めまして。
管理人の馬場です。
返信が遅れてしまいまして申し訳ありません。
季節成分の入れ方ですが、ダミー変数と三角関数において、明確な優劣はありません。
そのため、どちらを使ってもよいということになります。
三角関数を使うと、滑らかな季節変動を表すことができます。
(ダミー変数ですと、どうしてもカクカクした季節変動になります)
一方、ダミー変数を使うと「月、火、水、木、金、土日」といったように、土日だけ同じ影響を持つと仮定して、週次の周期性を表すことなどもでき、応用範囲が広いです。
あいまいな回答で申し訳ないですが、ご自身の解析対象となるデータに合わせるしかないのかなと思います。
よろしくお願いします。
はじめまして。
いつもこちらのサイトで勉強させてもらっております。
ダミー変数を使う方法はPyhonのstatsmodelで実現可能なでしょうか?
よろしくお願いします。
返信が大変遅れてしまい、すいませんでした。
以下のマニュアルを見ると、ダミー変数を使うものと三角関数を使うものをSeasonalとCycleで使い分けることができるようです。
http://www.statsmodels.org/stable/generated/statsmodels.tsa.statespace.structural.UnobservedComponents.html