KFASの使い方
新規作成:2018年2月7日
最終更新:2018年2月7日
ローカルレベルモデルの推定を通して、KFASパッケージの使い方を説明します。
この記事は、書籍「時系列分析と状態空間モデルの基礎:RとStanで学ぶ理論と実装」の一部を公開したものです。
この書籍は時系列分析の基礎の基礎から始めて、Box-Jenkins法や一般化状態空間モデルまでを解説した、初学者のための時系列分析の入門書です。
類書と比べると難易度は低めだと思っておりますので、これから時系列分析を始めてみたいと考えている方にお勧めします。
|
時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装 ハヤブサの表紙が目印です。 サポートページはこちらです。コードもこちらからダウンロードできます。 |
 |
スポンサードリンク
目次
- この章で使うパッケージ
- 分析の対象となるデータ
- KFASによる線形ガウス状態空間モデルの推定
- 推定結果の図示
- KFASによる状態の推定と信頼・予測区間
- KFASによる予測
- 補足:ローカルレベルモデルにおける予測
- 補足:補間と予測の関係
この章で使うパッケージ
この章で使う外部パッケージの一覧を載せておきます。この章では断りなくこれらの外部パッケージの関数を使用することがあります。パッケージのインストールはすでに行われているとします。
library(KFAS) library(ggplot2)
分析の対象となるデータ
この章でも、ナイル川の流量データを分析の対象とします。
ただし、最後の20年間は予測におけるテストデータとします。
nile_train <- window(Nile, end = 1950)
さらに、途中20年間に、欠損があったとします。NAは欠損を表す記号です。
nile_train[41:60] <- NA
KFASによる線形ガウス状態空間モデルの推定
KFASを用いてローカルレベルモデルを推定してみます。
欠損値があったとしても、気にすることなくモデルを推定することが可能です。
# Step1:モデルの構造を決める
build_kfas <- SSModel(
H = NA,
nile_train ~ SSMtrend(degree = 1, Q = NA)
)
# Step2:パラメタ推定
fit_kfas <- fitSSM(build_kfas, inits = c(1, 1))
# Step3、4:フィルタリング・スムージング
result_kfas <- KFS(
fit_kfas$model,
filtering = c("state", "mean"),
smoothing = c("state", "mean")
)
●Step1 モデルの構造を決める
第2章で学んだ、状態方程式・観測方程式によりモデルの構造を指定します。
このとき、SSModelという関数を使用します。この関数の中にモデルの構造を指定していきます。
Hは観測誤差の分散を表しています。Qは過程誤差の分散を表しています。『H = NA』などとすることによって、当該パラメタが「不明な値」であるとみなしてパラメタ推定をしてくれるようになります。
モデルの構造を指定しているのは『nile_train ~ SSMtrend(degree = 1, Q = NA)』の部分です。SSMtrendはトレンドモデルを構築する関数で、次数を1にすることでローカルレベルモデルを指定していることになります。
状態空間モデルはローカルレベルモデル以外にも様々な表現でデータを表すことができます。それらに対応するKFASの関数も豊富にあります。
■SSMtrend
degree = 1ならローカルレベルモデル
degree = 2ならローカル線形トレンドモデルを組むことができます。
例:SSMtrend(degree = 2, c(list(NA), list(NA)))
■SSMseasonal
季節変動を表すことができます。
period = 12とすることで月単位データのように12か月周期となります。
sea.type = “dummy”ならダミー変数を用います。
sea.type = ” trigonometric”なら三角関数を用います。
例:SSMseasonal(period = 12, sea.type = “dummy”, Q = NA)
■SSMregression
外生変数を組み込むことができます。時変係数のモデルにも対応しています。
例:SSMregression( ~ 外生変数 , Q = NA)
■SSMarima
ARIMAモデルと同等のモデルを推定することができます。
■複数の要素が入ったモデルを作る
以下のようにして、複数の要素を足し合わせることができます。
build_sample <- SSModel(
H = NA,
対象データ ~
SSMtrend(degree = 1, Q = NA) + # ローカルレベルモデル
SSMregression( ~ 外生変数 , Q = NA) # 外生変数
)
●Step2 パラメタ推定
fitSSM関数を用いることで、最尤法によるパラメタ推定ができます。
引数の『inits = c(1, 1)』に注目してください。これは「テキトー」に決めたパラメタ(過程・観測誤差の分散)です。「テキトー」なパラメタを最尤法で修正するわけです。最初に決めた「テキトー」なパラメタをパラメタの初期値と呼びます。
状態の初期値については散漫初期化という解決策があったのですが、パラメタの初期値は良い方法がなく、勘で決めてやるしかありません。ローカルレベルモデルくらいの簡単なモデルでは大きな影響は出ませんが、複雑なモデルになると、初期値への依存性が出てくることがあります。初期値をいくつかのパターンで試してみて、最も尤度が高くなった結果を採用するのがベターです。
KFASの場合、推定結果は大きく$optim.outと$modelに分かれています。前者が推定されたパラメタ、後者が「最適なパラメタを用いて組みなおされたモデル」となっています。dlmパッケージと異なり、モデルを組みなおす必要はありません。この点で見ても、KFASのほうが短いコードで実装できることがわかります。
組みなおされたモデル(fit_kfas$model)の持つパラメタを確認してみます。Hは観測誤差の分散です。Qは過程誤差の分散です。
> # 観測誤差の分散
> fit_kfas$model$H
, , 1
[,1]
[1,] 12782.35
> # 過程誤差の分散
> fit_kfas$model$Q
, , 1
[,1]
[1,] 2489.915
●Step3,4 フィルタリング・スムージング
KFS関数を用いることでフィルタリングも平滑化も同時に実行できます。
フィルタリングだけでいい、という場合は『smoothing = “none”』のように、明示的に使わないと指定しておきます。
以下のように結果を保存しておきます。
# フィルタ化推定量 mu_filter_kfas <- result_kfas$a[-1] # 平滑化推状態 mu_smooth_kfas <- result_kfas$alphahat
KFS関数の結果において『$a』に状態の1期先予測値が『$alphahat』に平滑化状態が格納されています。1期先予測値は、まだ当期の観測値を用いた補正(フィルタリング)が行われる前の値であることに注意してください。
ただし前期の観測値を用いたフィルタリングは行われています。そのため『$a』は前期のフィルタ化推定量であるとみなすことができます。1時点ずれているので、最初の値(観測値がまだ得られていない0時点目のフィルタ化推定量)を[-1]として切り捨てています。切り捨てられた部分は、散漫初期化されているので意味がない値です。
推定結果の図示
フィルタ化推定量を図示してみましょう。autoplot関数を用いる方法もありますが、細かい指定が難しいので別の方法を使います。まずはデータを整形します。
df_filter <- data.frame( y = as.numeric(Nile[1:80]), time = 1871:1950, mu_filter = mu_filter_kfas )
ggplot関数を用いて図示します。
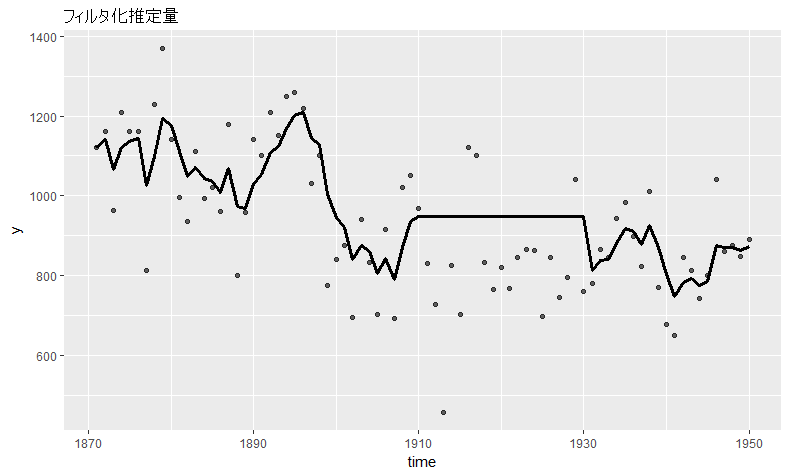
ggplot(data = df_filter, aes(x = time, y = y)) + labs(title="フィルタ化推定量") + geom_point(alpha = 0.6) + geom_line(aes(y = mu_filter), size = 1.2)
ggplotで外枠を作り、labsでタイトルを追加します。以下も「+」記号を使ってgeom_point(観測値の散布図)、geom_line(フィルタ化推定量の折れ線図)を足していきます。alphaは色の濃さの指定です。
1910~1930年の欠損があった年は、状態の値がずっと同じになっていることがわかります。これがローカルレベルモデルの補間の特徴です。
スポンサードリンク
KFASによる状態の推定と信頼・予測区間
平滑化状態と、その信頼区間と予測区間を求めます。
厳密な定義ではありませんが、信頼区間と予測区間の違いのイメージは以下のようなところです。
● 信頼区間:状態がこの間に収まるだろう区間
● 予測区間:観測値がこの間に収まるだろう区間
予測区間には、観測誤差の大きさも加味されていることだけ覚えてください。
まずはpredict関数を使って信頼区間を求めてみます。
『interval = “confidence”』と指定すると信頼区間となります。『level = 0.95』と指定すると95%信頼区間になります。
smooth_conf <- predict( fit_kfas$model, interval = "confidence", level = 0.95)
結果はこちらです(Start、End、Frequencyの出力は省略しています)。
> head(smooth_conf, n = 3)
fit lwr upr
[1,] 1113.876 981.9267 1245.826
[2,] 1112.683 996.8118 1228.555
[3,] 1102.274 993.8005 1210.747
予測区間を求めてみます。『interval = “prediction”』と指定するだけで予測区間に変わります。
smooth_pred <- predict( fit_kfas$model, interval = "prediction", level = 0.95)
結果はこちら。幅が広くなっていることに注目してください。
> head(smooth_pred, n = 3)
fit lwr upr
[1,] 1113.876 855.9740 1371.779
[2,] 1112.683 862.6252 1362.742
[3,] 1102.274 855.5566 1348.991
なお、predict関数のfitの値は平滑化状態の値がそのまま入っています。
> head(mu_smooth_kfas) [1] 1113.876 1112.683 1102.274 1118.993 1117.986 1108.794
KFASによる予測
predict関数において『n.ahead = 20』と指定することで、20時点先まで予測することができます。予測区間も併せて計算しておきました。
forecast_pred <- predict( fit_kfas$model, interval = "prediction", level = 0.95, n.ahead = 20)
これも図示してみましょう。
その前に、平滑化状態と予測結果を結合させます。rbindは行を結合する関数です。
estimate_all <- rbind(smooth_pred, forecast_pred)
続いて、図示のためのデータをまとめます。cbindは列を結合する関数です。
df_forecast <- cbind( data.frame(y = as.numeric(Nile), time = 1871:1970), as.data.frame(estimate_all) )
最後に図示のためのコードを書きます。geom_ribbonを用いると、最大値と最小値を指定することで、その範囲を網掛けにすることができます。
ggplot(data = df_forecast, aes(x = time, y = y)) + labs(title="平滑化状態と将来予測") + geom_point(alpha = 0.5) + geom_line(aes(y = fit), size = 1.2) + geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.3)
平滑化状態においては、欠損値は「欠損前と後のデータを直線でつないだもの」となっています。
1950年以降は予測値となっています。将来予測の結果はずっと横バイとなっていることに注目してください。また、予測区間は年を追うたびに広くなっていきます。
補足:ローカルレベルモデルにおける予測
ローカルレベルモデルにおける予測の方法をおさらいしておきます。
将来予測値の点推定値は、最新年の状態の値と全く同じで変化しません。
> tail(smooth_pred, n = 1)
fit lwr upr
1950 872.5365 614.6343 1130.439
> head(forecast_pred, n = 5)
fit lwr upr
1951 872.5365 596.7133 1148.360
1952 872.5365 579.8876 1165.185
1953 872.5365 563.9781 1181.095
1954 872.5365 548.8497 1196.223
1955 872.5365 534.3974 1210.676
次は予測区間がどのように広がっていくのかを確認します。『se.fit = T』と指定することで、予測区間の標準偏差を取得することができます。
forecast_se <- predict( fit_kfas$model, interval = "prediction", level = 0.95, n.ahead = 20, se.fit = T)[, "se.fit"]
標準偏差を2乗すると分散になりますね。
> forecast_se^2 [1] 7022.231 9512.146 12002.060 14491.975 16981.890 19471.805 [7] 21961.720 24451.635 26941.550 29431.465 31921.380 34411.295 [13] 36901.209 39391.124 41881.039 44370.954 46860.869 49350.784 [19] 51840.699 54330.614
差分をとると、分散は毎時点2489.915ずつ増えていることがわかります。
> diff(forecast_se^2) [1] 2489.915 2489.915 2489.915 2489.915 2489.915 2489.915 2489.915 [8] 2489.915 2489.915 2489.915 2489.915 2489.915 2489.915 2489.915 [15] 2489.915 2489.915 2489.915 2489.915 2489.915
分散の増加量は「過程誤差の分散」の値と一致します。
> fit_kfas$model$Q
, , 1
[,1]
[1,] 2489.915
過程誤差が積み重なっていくため、長期の予測は当たりにくくなるということを確認してください。
補足:補間と予測の関係
状態空間モデルでは、欠損値の補間と未来の予測はまったく同じ枠組みで計算をすることができます。そのことを確認しておきましょう。
まずは、未来の値を欠損として、モデルを組んでみます。このモデルにおいて「補間」をすると、予測をしたことと同じ結果になるはずです。
# 未来の値をNAとしたもの nile_na <- Nile nile_na[81:100] <- NA build_kfas_na <- SSModel( H = NA, nile_na ~ SSMtrend(degree = 1, Q = NA) ) fit_kfas_na <- fitSSM(build_kfas_na, inits = c(1, 1))
次は、データの長さそのものを短くします。
# 未来の値を切り捨てたもの nile_split <- window(Nile, end = 1950) build_kfas_split <- SSModel( H = NA, nile_split ~ SSMtrend(degree = 1, Q = NA) ) fit_kfas_split <- fitSSM(build_kfas_split, inits = c(1, 1))
両者の「補間」と「予測」の結果が一致することを確認します。
> hokan <- predict( + fit_kfas_na$model, interval = "confidence", level = 0.95)[81:100,] > yosoku <- predict( + fit_kfas_split$model, interval="confidence", level=0.95, n.ahead= 20) > all(hokan == yosoku) [1] TRUE
なお『==』という演算子は、2つの値が等しければTRUEを返します。allはすべての結果がTRUEだった場合のみTRUEを返します。補間と予測が完全に一致していることがわかります。
参考文献
|
時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装 この記事の作者が書いた書籍です。 ハヤブサの表紙が目印です。 サポートページはこちらです。コードもこちらからダウンロードできます。 |
 |
スポンサードリンク



いつも書籍を参考にさせていただいております。
周りに聞ける方がいないので、わかりやすく、大変助かっております。
一点質問があるのですが、今ローカル線形トレンドモデル+季節性+外生変数(ダミー変数)を入れたモデルを作っていて、何点か先の予測と95%信頼区間を出そうとしています。
ですが、ほとんどfit,lwr,uprの値がほとんど同じ値で、95%の幅がない状態になります。
かなり先まで予測しているので信頼区間の幅が広がってほしいのですが、なにか原因となりうるものはあるでしょうか?
コメントありがとうございます。
管理人の馬場です。
データを見ていないので、原因まではちょっとわかりませんが、
一般論としては、コードのミスでない限り、
過程誤差の分散がとても小さいのではないかと思います。
例えば、純粋な正規ホワイトノイズを対象としてモデル化して予測する場合、
定常過程ですので、長期予測になっても、予測の幅は広くなっていきません。
参考になれば幸いです。
いつも参考にさせて頂いてます。
解説がわかりやすくて、本当に助かります。
1点質問があります。
次の観測を予測するモデルではなく、n時点先を予測するモデルをつくりたいのですが
KFASで実装する方法をご存知ありませんか?
alt様
コメントありがとうございます。
管理人の馬場です。
「KFASによる予測」という節でも解説していますが、
predict関数において『n.ahead = 20』と指定することで、20時点先まで予測することができます。
こちらの機能を使ってn時点先を予測すればよいかと思います。
書籍を購入させて頂きました。また、ブログもわかりやすく、参考にさせていただいております。
現在、ローカル線形トレンドモデルで周期性12でモデルをチャレンジしております。
その際にでてくる変数の意味合いについて伺いたく質問をさせていただきます。
具体的に伺いたい点が2つあります。
①モデル設定時の変数について
例として下記コードを記載されておりますが、c以降の2つのパラメータは過程誤差のどのような項目を推定しているのでしょうか?
SSMtrend(degree = 2, c(list(NA), list(NA)))
②平滑化推状態の変数について
mu_smooth_kfas <- result_kfas$alphahat 結果のデータの中身を確認すると、
levelとslopeの2つ変数と季節性のダミー変数が追加さえれておりました。
このlevelとslopeはどのような意味合いを持つ変数になりますでしょうか?
アドバイスをいただけますとこれからの励みになります。
何卒、よろしくお願いいたします。
———————————————————————————————-
私が設定してモデル構造は下記になります。
# Step1:モデルの構造を決める
build_kfas <- SSModel(
H = NA,
nile_train ~ SSMtrend(degree = 2, Q = c(list(NA), list(NA))) +
SSMseasonal(period = 12, sea.type="dummy", Q=NA))
けいすけ様
コメントありがとうございます。
管理人の馬場です。
返信が遅れて失礼しました。
書籍をご購入いただきありがとうございます。
以下は「時系列分析と状態空間モデルの基礎」のページ数を指し示しながら回答します。
①モデル設定時の変数について
p259が参考になるかと思います。
Qは過程誤差の分散を表すものです。
c(list(NA), list(NA))と「NA」を指定することで、分散が未知であることを想定したモデルを作っています。
1つ目のNAは水準の変動の大きさで、2つ目はトレンドの変動の大きさで鵜s。
②平滑化推状態の変数について
levelは水準成分を表しています。
slopeはトレンド成分を表しています。
p259の数式でいうと、levelはμであり、slopeはδに対応します。
p260の実行結果も併せて参照してください。
参考になれば幸いです。