重回帰分析
前のページで変数選択 ができたので、実際の予測を行います。
目次
1.使用データとモデリング
2.AICによるモデル選択
3.予測
1.使用データとモデリング
set.seed(0)
N<-100
Intercept<-5
B1<-10
B2<-5
x1<-sort(rnorm(N,sd=2))
x2<-rnorm(N,sd=2)
e<-rnorm(n=N,sd=3)
y<-Intercept+B1*x1+B2*x2+e
上記 のデータは前ページの モデル選択と同じデータです。なので、同じ推定結果が出るはずです。交互作用も含めたmodel3を作ります
model3<-lm(y~x1*x2)
2.AICによるモデル選択
検定によるモデル選択は前のページを見てください。ここではAICによるモデル選択のみを行います。
パッ ケージMuMInをダウンロードしてから(http://mumin.r -forge.r-project.org/ )
library(MuMIn)
kekka.AIC<-dredge(model3,rank=”AIC”)
all.model <- get.models(kekka.AIC)
best.model<-all.model[1]
> best.model
$`4`
Call:
lm(formula = y ~ x1 + x2)
Coefficients:
(Intercept) x1 x2
5.202 9.973 4.986
どのモデルが最適かが分かったので、またモデルを作りなおします。
model2<-lm(y~x1+x2)
model2 が最適なモデルになります。これで予測を行います。
3.予測
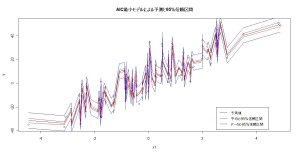
A<-predict(model2,se.fit=T,interval=”confidence”) #推定平均の95%推定区間付き
B<-predict(model2,se.fit=T,interval=”prediction”) #推定データの95%推定区間付き
plot(x1,y,main=”AIC最小モデルによる予測と95% 信頼区間”)
lines(x1,A$fit[,1],lwd=1)
lines(x1,A$fit[,2],col=”red”)
lines(x1,A$fit[,3],col=”red”)
lines(x1,B$fit[,2],col=”blue”)
lines(x1,B$fit[,3],col=”blue”)
legend(2.5,-20,c(“予測値”,”平均の95%信頼区間”,”データの95%予測間”),col=c(1,2,4),lwd=1)
ちなみに、シミュレーションデータを作る際、さりげなくx1<-sort(rnorm(N,sd=2))と していましたが、 sort をしておかないと、とても見難いグラフになってしまいます。ちなみに sort とは、昇順並び替え関数です。
参 考文献[1]
山田作太郎・北田修一:生物統計学入門、第7章 回帰分析
前のページへ ⇒ モデル選択理論編
次のページへ ⇒ 平滑化スプラインと加法モデル