成長曲線

最終更新:2015年11月22日

魚は、大きくなって価値が高くなってから取るのが ベスト。小さいものは獲らず、成長するまで待つことが肝心です。

でも、いったいどれくらい待てばいいの？
雌雄によって待つ時間は変えたほうがいいの？　一緒でいいの？

この問いに答えるために、魚の成長の特徴を調べ る。これが成長曲線の推定と言う代物です。

サンプルデータとRパッケージ

今回もこまかい理屈は置いておいて、Rを使ってvon Bertalanffyの成長曲線を推定します。さらに、雌雄によって成長曲線が異なるとみなせるかを検定するところまで行います。

今回はパッケージFSAを用います。

コードをコピペする際はこちらのソースコード一式をご利用されると便利です。

FSAは「パッケージのインストール」からは落とせません。FSAをインストールするには、以下のコードを実行します。ただし、やや時間がかかります。

基本的にはこのページに書かれていることだけで事足りますが、細かいことは
http://www.rforge.net/FSA/Installation.html
も参考にしてください（英語です）。

パッケージのインストールの手順を説明します。
まずは、Rを右クリックして「管理者として実行」します。そのうえで以下のコードを実行。

source(“http://www.rforge.net/FSA/InstallFSA.R”)

上記のコードはVPAのページでも使ったsource関数を使っています。ウェブサイトにUPされているRファイルをよみこんで実行してね、という指示です。

もしもうまくいかなかった場合はhttp://www.rforge.net/FSA/InstallFSA.Rから直接スクリプトをコピペしてRのエディタに張り付けてから実行してください。

さらに、データを読み込むために以下を実行する必要もあります。

install.packages(“FSAdata”,repos=”http://www.rforge.net/”,type=”source”)

パッケージをインストールする際に国の名前が表示された場合は、Japanならどこでもよいので3つくらいあるJapanのなかから好きなものを選んでダブルクリックしてください。そうしたら、パッケージのインストールが完了します。

パッケージのインストールが完了したら、以下のコードを実行して、パッケージを使用する下準備をします。

library(FSA)
library(FSAdata)
library(nlstools)

これでようやっと計算に映ることができます。
FSAパッケージは、私はあまり使ったことはありませんが水産資源解析関連のいろいろな関数があるようなので、興味のある方は調べてみてください。

パッケージFSAdataの中に入っているCroaker2と言うデータを用います。
どんなデータか見てみます。

 # データの読み込みとデータの表示
data(Croaker2)
head(Croaker2)

#　性別ごとの体長データの要約
tapply(Croaker2$tl,Croaker2$sex,summary)

#　性別ごとに分けた年齢体長関係
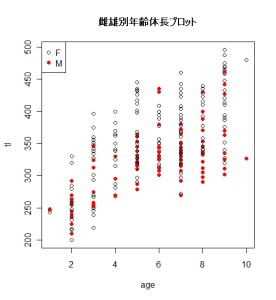
plot(tl~age,pch=c(21,19)[Croaker2 $sex],col=c(1,2)[Croaker2$sex],
data=Croaker2,main=”雌雄別年齢体長プロット”)
legend(“topleft”,legend=c(“F”,”M”),pch=c(21,19),col=c(1,2))

結果はこちら

> head(Croaker2)
age tl sex
1 1 243 F
2 1 247 F
3 1 248 M
4 2 330 F
5 2 320 F
6 2 285 F
> tapply(Croaker2$tl,Croaker2$sex,summary)
$F
Min. 1st Qu. Median Mean 3rd Qu. Max.
200.0 326.5 352.0 358.9 410.0 496.0

$M
Min. 1st Qu. Median Mean 3rd Qu. Max.
210.0 292.0 325.0 319.6 343.8 462.0

tapplyの結果や、グラフを見ると、雌の方が若干大きそうな感じがします。

と言うことで、雄雌一緒にしたデータと、雌雄別のデータの両方を用いて、成長曲線がどう変わるか比較していきましょう。雌雄で分けるためのプログラムはこちら。

Croaker.M <- subset(Croaker2,sex==”M”)
Croaker.F <- subset(Croaker2,sex==”F”)

データの準備ができたので、次からは実際に成長曲線を推定していきましょう。

 

von　Bertalanffy　曲線の推定

上のデータを用いて、代表的な成長曲線の一つである　von　Bertalanffy　曲線を推定してみます。

# 初期値の設定　FSAパッケージより
start.full <- vbStarts(tl~age,data=Croaker2,type=”typical”)
start.full

# 雌雄まとめたモデル
Bertalanffy.full<-nls(tl~Linf*(1-exp(-K*(age-t0))),data=Croaker2,start=start.full)
overview(Bertalanffy.full)

#雌雄別モデル
Bertalanffy.M<-nls(tl~Linf*(1-exp(-K*(age-t0))),data=Croaker.M,start=start.full)
Bertalanffy.F<-nls(tl~Linf*(1-exp(-K*(age-t0))),data=Croaker.F,start=start.full)

#　プロット
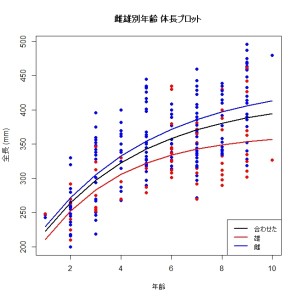
plot(tl~age,xlab=”年齢”,ylab= “全長 (mm)”,pch=16,col=c(4, 2)[Croaker2$sex],
data=Croaker2,main=”雌雄別年齢 体長プロット”)
lines(c(1,2,3,4,5,6,7,8,9,10),predict(Bertalanffy.full,
new=data.frame(age=c (1,2,3,4,5,6,7,8,9,10))),lwd=2)
lines(c(1,2,3,4,5,6,7,8,9,10),col=2,predict(Bertalanffy.M,
new=data.frame(age=c (1,2,3,4,5,6,7,8,9,10))),lwd=2)
lines(c(1,2,3,4,5,6,7,8,9,10),col=4,predict(Bertalanffy.F,
new=data.frame(age=c (1,2,3,4,5,6,7,8,9,10))),lwd=2)
legend(“bottomright”,legend= c(“合わせた”,”雄”,”雌”),lwd=2,col=c(1,2,4))

文献3を見ると、重み付き最小二乗法を使った方がよさそうな気がしましたが、今回は重みを設定していません。重み付き最小二乗法を するならば、nls（）の中にweightsを指定してやる必要があります。

成長曲線は、非線形のモデルに最小二乗法を当てはめて推定するわけですが、毎回初期値をどうしようかと言うことで悩みます。そこで、vbStarts(tl~age,data=Croaker2,type=”typical”)を使いました。

これは、ワルフォードの定差図を使ってパラメータを推定する関数です。ワルフォードの定差図による推定は統計的な誤りがあるので本来は使ってはなりませんが、非線形モデルを推定するための初期値にこれを使ったわけです。FSAの説明書（http://www.rforge.net/doc/packages/FSA/vbStarts.html）
にもこの初期値は余り信用しすぎるなと書かれてあります。この値だけを信用すべきと言う確固たる理由は特にないようです。でも、正確な値と割と近そうな初期値を選べるということで、今回も採用しました。

今回は雌雄を差別しないモデル以外では省略しましたが、overview (モデル)でモデルの詳細を見ることができます。こちらはパッケージnlstoolsの関数で、パラメータの95%信頼区間な ども表示してくれます。

overviewの結果はこんな感じ。

> overview(Bertalanffy.full)

——
Formula: tl ~ Linf * (1 – exp(-K * (age – t0)))

Parameters:
Estimate Std. Error t value Pr(>|t|)
Linf 416.25682 19.34549 21.517 < 2e-16 ***
K 0.24180 0.06242 3.874 0.00013 ***
t0 -2.17074 0.85673 -2.534 0.01177 *
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 45.33 on 315 degrees of freedom

Number of iterations to convergence: 7
Achieved convergence tolerance: 5.744e-06

——
Residual sum of squares: 647000

——
Asymptotic confidence interval:
2.5% 97.5%
Linf 378.1941202 454.3195283
K 0.1189993 0.3646082
t0 -3.8563825 -0.4851029

——
Correlation matrix:
Linf K t0
Linf 1.0000000 -0.9637788 -0.8779838
K -0.9637788 1.0000000 0.9674683
t0 -0.8779838 0.9674683 1.0000000

最後のプログラムで、以下のような図が描けます。

 

雌雄で成長曲線に差があるか、検定

F検定で、成長曲線の雌雄差の有無を検定します。

Smf<-deviance(Bertalanffy.full)
Sf<-deviance(Bertalanffy.M)
Sm<-deviance(Bertalanffy.F)

F<- (Smf-Sm-Sf)/3 / ( (Sm+Sf)/(length(Croaker2$age)-3*2))

 

> F
[1] 20.24402

> 1-pf(F,3,length(Croaker2$age)-3*2)
[1] 5.166978e-12

RではExcelと異なり、推定されたモデルのパラメータをoverview関数で細かく見れます。また、F検定も比較的楽にできる のではないかと思います。

尚、重み付き最小二乗法で推定した場合には、F検定で無くχ2検定を行う必要があるようです。

 

文献

赤嶺達郎：水産資源解析の基礎， 恒星社厚生閣, 2007年

FSAのページ（FSA – Fisheries stock assessment methods.）
http://www.rforge.net/FSA/index.html