VARモデル
最終更新:2016年1月24日
Rを用いたVARモデルの簡単な解説と計算方法を載せます。
目次
1.VARモデルとは
2.VARモデルの仕組み
3.VARな予測
4.VARあれこれ
スポンサードリンク
1.VARモデルとは
以前紹介したのは1変量のARIMAモデルというものでした。
これは「過去の自分のデータから将来の自分を予測する」というものです。たとえば、2000年にサンマがたくさんいたら過去の2001年にもたくさんいることになるだろうという風に、サンマの予報をするなら、サンマの漁獲量だけに注目してして予測をします。
でも、去年餌になるプランクトンが多かったから今年はサンマが増えた、という風に、「ほかのやつら」の影響を受けているかもしれませ ん。
そんな場合をモデルで表して予測をしてやろうというのが今回扱うVARモデルというものになります。
2.VARモデルの仕組み
VARとは Vector Auto Regressive ⇒ベクトル自己回帰モデルの略です。まえにやったARモデルを多変量に拡張したものになります。
AR モデルとは、たとえばサンマの来遊量を予測しようとしたとき、前年のサンマ来遊量を横軸に、翌年のサンマ来遊量を縦軸においてプロットして回帰分析をやったのと大体同じものでした。これを多変量に応用します(名前の通り、MAモデルはVARにおいては加味されません。VARMAモデルは、一応あるにはありますが、あまり使われないし、省略します)。
具体的にはこんな感じ
VARモデル
今年のサンマ = 去年のサンマ×傾きA + 去年のプランクトン×傾きB +切片C
今年のプランクトン= 去年のプランクトン×傾きD + 去年のサンマ×傾きE +切片F
傾きとか切片っていうのは、回帰分析をイメージして書いてみました。φとか使うとややこしく見えますもんね。「傾きA」とか書いているのは、各々の傾きは別の値だよ(傾きAと傾きBは異なる)ということを見えやすくするために入れただけです。こういうパラメタはちゃんと全部別々に推定されます。
ここで、もしもサンマを一変量のARモデルで表したならば、こうなります。
ARモデル
今年のサンマ = 去年のサンマ×傾きG + 切片H
これにプランクトンの値が加味されただけ。簡単なんですけど、ほかのやつらの影響を組み込んだ方がうまく予測できそうな気がしますよね。
経済学とかだと、変数の間の関連性を調べる(サンマとプランクトンの関係とか)ためにさらにいろいろな解析が行われるみたいですが、今回は省略。予測だけをやります。
因果性の検定などの細かい話は、『銀座で働くデータサイエンティストのブログ』に大変丁寧に書かれてあるのを発見しましたので、こちらのサイト様をご覧になられることをお勧めします。
3.VARな予測
今回使うのは vars というパッケージです。
これをRの左上にある「パッケージ」→「パッケージのインストール」をやってインストールしてから
library(vars)
をやれば準備完了。これを使えば例によってAICを使って簡単にモデル選択ができます。モデル選択についてはこちらをみてく ださい。
このモデルの場合は、「何期前までを使って予測するか?」(モデルの次数とか言ったりします)をAICを使って選ぶということになります。どの変数を使って予測すればよいかということは分かりません。予測に効く変数かどうかはGrangerの因果検定をやれば調べられますが、今回は省略します。
今回は、このパッケージに入っているCanadaを使います。なんかよくわかりませんが経済データだそうです。マニュアルの例でも紹 介されていたデータなのでそのまま使いました。四つの変数が入ってます。
data(Canada)
中身はこちら
> Canada
e prod rw U
1980 Q1 929.6105 405.3665 386.1361 7.53
1980 Q2 929.8040 404.6398 388.1358 7.70
1980 Q3 930.3184 403.8149 390.5401 7.47
1980 Q4 931.4277 404.2158 393.9638 7.27
1981 Q1 932.6620 405.0467 396.7647 7.37
1981 Q2 933.5509 404.4167 400.0217 7.13
1981 Q3 933.5315 402.8191 400.7515 7.40
1981 Q4 933.0769 401.9773 405.7335 8.33
・・・・・・略
Canadaの1999以降は切って、テスト用に残しておきます。window()関数を使えば簡単に切れます。
Canada.1998<-window(Canada,end=c(1998,4))
で、VARモデルを推定する関数は文字通りVAR ()というやつです。次数の決定はVARselect ()でOK。データはトレンド付かトレンド無かを選ぶことができます。
トレンドなし、定数付(切片が0でない)で最適な次数を調べます。
> VARselect(Canada.1998, lag.max = 5, type=”const”)
$selection
AIC(n) HQ(n) SC(n) FPE(n)
3 2 1 3$criteria
1 2 3 4 5
AIC(n) -5.968164387 -6.316081011 -6.385300206 -6.112389835 -5.87693104
HQ(n) -5.714700702 -5.859846377 -5.726294624 -5.250613305 -4.81238356
SC(n) -5.330789774 -5.168806707 -4.728126212 -3.945316150 -3.19995766
FPE(n) 0.002561326 0.001816949 0.001714569 0.002300861 0.00301527
AIC基準では次数3が最もよさそうということになりました。この結果を用いてVARモデルを推定します
lag1 <- VARselect(Canada.1998, lag.max = 5, type=”const”)$selection[1]
var.1 <- VAR(Canada.1998, p=lag1, type=”const”)
計算結果は長いので略。 var.1 と打ち込めばモデルの傾き(係数)とかいろいろ出てきます。
予測します。
yosoku <- predict(var.1, n.ahead = 8, ci = 0.95, dumvar = NULL)
kekka <- ts(yosoku$fcst$e[,1], start=1999, frequency=4)
sita <- ts(yosoku$fcst$e[,2], start=1999, frequency=4)
ue <- ts(yosoku$fcst$e[,3], start=1999, frequency=4)
これで、Canadaデータのうちeという変数に関する予測とその95%区間が求まります。
普通にpredict関数を使えば予測できます。n.ahead=8なので、8期先まで予測するという指定になっています。ciはConfidence intervalの略で、信頼区間の設定です。0.95なので95%区間ですね。
あとはyosokuという変数の中に入っている予測値・95%下限地・95%上限値を抽出してkekkaだのue、sitaだのに格納をしました。
プロットします。
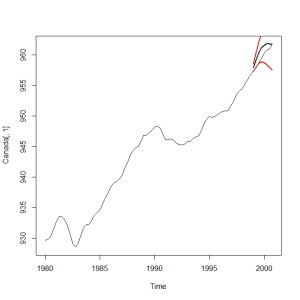
ts.plot(Canada[,1])
lines(kekka,type=”l”,col=1,lwd=2)
lines(ue,type=”l”,col=2,lwd=2)
lines(sita,type=”l”,col=2,lwd=2)
まぁまぁいけてそうです。
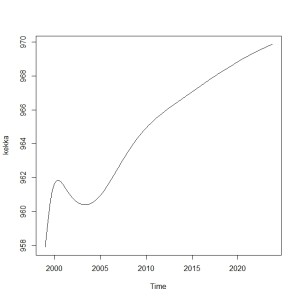
遠い先まで予測してみます(実用性はたぶんありません。予測結果の特徴を見るためのものです)
yosoku<-predict(var.1, n.ahead = 100, ci = 0.95, dumvar = NULL)
kekka<-ts(yosoku$fcst$e[,1],start=1999,frequency=4)plot(kekka)
長期予測のやり方としては、サンマとプランクトンの例で行くと、
1 過去のサンマとプランクトンからサンマを予測
2 同様にプランクトンも予測
3 予測されたサンマ・プランクトンからサンマを予測
4 同様にプランクトンを・・・・・・という手順です。
まぁRが勝手にやってくれるんで知らなくていいかもしれませんが。でも、長期予報はあんまりあてにならない(予測結果を使って予測するわけだから)というのは直感的にわかるでしょう。
同様にトレンド付のモデルも推定できます。
lag2<-VARselect(Canada.1998, lag.max = 5, type=”both”)$selection[1]
var.2<-VAR(Canada.1998,p=lag2,type=”both”)
結果は省略。bothっていうのは、切片と傾き両方入ったモデルだと考えてください。
ちなみに、普通の教科書では傾きは係数、切片は定数項という名前で書かれていることが多いと思います。
4.VARあれこれ
実はVARモデルは前に書いたARMAモデルで記述することができます。数式の上ではそうなんですが、実感わかないですね。ここら辺は山本 拓 先生の参考文献がわかりやすいです(関係ないけれども、ARモデルとMAモデルの変換などもこの文献がわかりやすかった。実例があるので)。でも、ARMAだとかなり長い次数が必要なのがVARだととても少なくて済むようです。
多変量ARだからMultiple ARでMARかとおもいきやVARという名称。ここら辺は数式見ないと実感できないかもしれません。B(モデル名)でベクトル表示して係数を見ることができます。なれたらこっちの方が見やすいかもしれません。
扱う変数の数が増えると(たとえばサンマとプランクトンだけではなくイワシとアジとサメと海鳥も追加とか)推定すべきパラメータ(傾き)がものすごい量になってしまうのであまり実用性がなくなってしまうので注意。
VAR のパワーアップバージョンでSVARとかがあります。これはVARモデルだと「過去が今に影響を与えている」ということしかモデルで表せられなかったのが、SVARだと「同じタイミングでもサンマとプランクトンは影響し合っている」ということを明示的にモデリングできます。同じくパッケージvarsで計 算できます。これ以外にもたくさん発展形があります。
あと、ベイズつかってパラメタ推定もできます。パッケージMSBVARで計算できます。
参考文献
|
経済・ファイナンスデータの計量時系列分析 (統計ライブラリー) このサイトで時系列解析関連の記事を書く際は必ず参照している本です。 時系列解析の基本となる考え方から始めて、モデルの詳しい説明まで載っています。 今、時系列解析を学びたいと思った方はこの本から入ると良いでしょう。 |
 |
|
Rによる計量経済分析 Rを使って計量経済分析を行う方法が書かれた本です。 VARをはじめとした時系列分析がコード付きで載っています。 「経済・ファイナンスデータの計量時系列分析」で仕組みを学び、この本で実装方法を学ぶと良いでしょう。 |
 |
書籍以外の参考文献
●山 本 拓:時系列分析とその経済分析への応用、大蔵省財政金融研究所「フィナンシャル・レビュー」
→時系列分析を最初に学ぶにあたっての、大変おすすめな資料です。ここまで丁寧な説明がネットで拾えるのはありがたいですね。PDF資料へのリンクも張っておきます。
PDFへのリンク
●松本 惇: 統計ソフトRによるVAR入門
●varsマニュアル: http://cran.r-project.org/web/packages/vars/vars.pdf
●銀座で働くデータサイエンティストのブログ
http://tjo.hatenablog.com/
→こちらのサイト様はVAR以外にも時系列分析関連の話題が結構多いです。やや数式が散見されますが、それでも非常に分かり易いほうだと思うのでお勧め。
スポンサードリンク


ご存知の範囲で下記に2点教えていただければ幸いです。
1.VARモデルに機械学習を応用
現在VARモデルで予測しているものを機械学習に置き換えて予測精度が向上するかを検証したく考えております。
時系列モデルに機械学習を適用という趣旨の解説は多く見られるのですが、VARモデル(要は複数の時系列モデル)に対して機械学習を応用することは現在の技術で可能でしょうか。
2.単位根過程あり・なしデータを同時に扱う
単位根過程ありの時系列と、なしの時系列があった場合に、それらのグレンジャー因果性はどのように検証すればよいのでしょうか。両時系列とも差分系列とすればよいのでしょうか。
VARモデルにおいても同様に、どう扱えばよいのか気になります。
本サイト頻繁に拝見させて頂いております。類を見ない、分かりやすいご説明ありがとうございます。
L様
管理人の馬場です。
返信が遅れまして、失礼いたしました。
1.VARモデルに機械学習を応用
できるかできないか、ということであれば、これは可能かと思います。
SVMなどでちらほら見られます。
ただし、この手法の有効性は、ご指摘の通り、あまり評価がなされていないように感じます。
多変量時系列データに対して、非線形性を組み込みたいという場合は、カオス時系列分析の枠組みの活用も候補の一つかと思います。
2.単位根過程あり・なしデータを同時に扱う
例えば岩波データサイエンスVol6のp68~のVARモデルの解説においては、2変数において、片方を差分系列、片方を原系列として、Grangerの因果性検定を行っています。
Granger因果性検定のp値を正しく計算する、という目的での変換であれば、単位根を持つものだけに差分を取ればよいでしょう。
しかし結果の解釈には注意してください。
「変数Aと変数BでのGranger因果性」ではなく
例えば「変数Aと変数Bの増減量とのGranger因果性の検定」として解釈する必要があります。
半年以上ぶりに質問させていただきます。
>1.VARモデルに機械学習を応用
>できるかできないか、ということであれば、これは可能かと思います。
>SVMなどでちらほら見られます。
上記VAR×機械学習に関して、まずは手っ取り早く実行してみたいと考えているのですが、もしRかPythonで既にパッケージ化されてるものをご存知でしたら、ご教示いただけないでしょうか。
Wutsqa(2008)”THE VAR-NN MODEL FOR MULTIVARIATE TIME SERIES FORECASTING”のように、手法としてVAR-NNを紹介している文献はあるものの、それを実行できるようなコードが見当たらず四苦八苦しているため、このような質問をさせていただきました。
L様
コメントありがとうございます。
管理人の馬場です。
VAR-NNを実行するR/Pythonパッケージは、当方も知らないです。
先ほど検索したら「NlinTS」というVARNNを実行するパッケージがRにあるらしいですが、
私は使ったことが無いですし、使い物になるパッケージかどうかも不明です。
お役に立てず、申し訳ないです。
馬場様
いつもご丁寧にご回答いただきありがとうございます。
インパルス応答を計測するにあたって、質問がございます。
1.異常値への対応
片方の時系列に異常値があった場合はどのような前処理を行うことが考えられるでしょうか。
例えば国や都道府県のマクロ指標の時系列を扱う場合、3.11のような震災によってその時期のみ大きく減少していることがございます。これに対して何の前処理もなくインパルス応答を計算してしまうと、そこに大きく引っ張られてしまうかと思います。事実、そのままのデータを用いた場合と、前年翌年の平均で平準化したデータを用いた場合とで、インパルス応答を比較したところ結果が大きく異なりました。
このような事象に対処する方法として、何か適切なものがあるかをご存知でしたらご教示いただけないでしょうか。
岩波データサイエンスVol. 6では、欠損値に対して「2階のランダムウォークモデルによる平滑化」が行われておりますが、異常値に対しても同じ方法が有効なのでしょうか。
2.構造変化への対応
片方の時系列分析に構造変化があった場合はどのような前処理を行うことが考えられるでしょうか。
データを構造変化前後に分けて別々にインパルス応答を計算するなどアナログなやり方は思いつくのですが… より適切な方法をご存知でしたらご教示ください。
状態空間モデルやRにあるstl関数を用いて、もしくは対数差分を取ってトレンドを除去することは構造変化に対処したことにはならないでしょうか。
登場のたびにご質問で申し訳ないのですが、お時間のできた際にご返信いただけると幸いです。
L様
コメントありがとうございます。
管理人の馬場です。
1.異常値への対応
いろいろのやり方があるので一概には言いにくいです。
例えば「デフレと戦う――金融政策の有効性」という本では
(https://www.nikkeibook.com/item-detail/13484)
ダミー変数を使用していました。
地震直後の3~5月に「1」を立てるような使い方ですね。
原因がある程度わかる場合にはこのようなやり方もあります。
2.構造変化への対応
構造変化を前処理で対応できるかは難しいところです。
VARモデルをそのまま使うのではなく、
そもそも構造変化に対応したモデルを作ることも検討されると良いと思います。
(難易度は上がってしまうでしょうが。私は使用経験があまりないです)
いつもブログを拝見させて頂いております。本記事についてご質問させて頂きたいことがございます。
記事内で予測をされているデータですが、定常過程ではないようです。AR過程では定常過程になるようにデータを加工してから係数を推定するのが一般的ですが、VARモデルでは定常過程である必要はないのでしょうか?
よろしくお願い致します。
KK様
コメントありがとうございます。
管理人の馬場です。
定常であるべきか否かは、分析の目的によって変わります。
例えば、この記事では言及がありませんが、Grangerの因果性検定を行う場合は、定常性を満たす必要があります。
しかし、単に予測を出すだけであれば、定常性が満たされていなくても構いません。
馬場様
ご回答頂きありがとうございます。なるほど…VARモデルの推定自体には定常過程は必要条件ではないのですね。
仰る通りGrangerの因果性などの定常過程を前提とする解析などについて疑問に思った次第です。
引き続き、記事の更新を楽しみしております。