Stanによるベイズ推定の基礎

新規作成日:2015年12月5日
最終更新日:2016年9月22日
 

理論がわかっても、実践ができなければ意味がありません。
ここでは、Stanというフリーソフトを使って、ベイズ統計学をもとにしたパラメタ推定をパソコンで実行する方法を説明します。

ベイズとMCMCの組み合わせでもって統計モデルのパラメタを推定することができるのでした。この方法を、以下では「ベイズ推定」と呼ぶことにします。
ここでは、Stanを用いて統計モデルのパラメタのベイズ推定をする方法を説明します。

重要な点は、「Stanの使い方」を覚えるだけではうまくいかないということです。
Stanの内部で使われているのは乱数生成アルゴリズムです。乱数を生成してパラメタを推定するという行為は、最小二乗法なりで方程式を解き、パラメタを一発で推定するやり方とは大きく異なります。
その違いをぜひ理解なさってください。

コードをまとめたものはこちらにおいておきます。コピペする際はこちらをお使いください。

 

この記事はベイズ推定を応用して状態空間モデルを推定する一連の記事の一つです。
記事の一覧とそのリンクは以下の通りです。
・ベイズ統計学基礎
・ベイズと統計モデルの関係
・ベイズとMCMCと統計モデルの関係
・Stanによるベイズ推定の基礎
・Stanで推定するローカルレベルモデル

スポンサードリンク

 

目次

1．Stanとは
2．Stanのインストール
3．Stanを実行する流れ
4．今回推定する統計モデルの概要
5．ステップ1：Stanを使用する準備
6．ステップ2：統計モデルの記述
7．ステップ3：データの指定
8．ステップ4：ベイズ推定の実行
9．ステップ5：うまく推定されているかをチェック
10．ステップ6：結果の解釈
11．Stanの補足：事前分布について

 

1．Stanとは

Stanとは、ただで使える、MCMCのフリーソフトです。
ただで使えるソフトとしては、ほかにもWinBUGSなどがありますが、Stanのほうがパラメタの収束がよいようです。
MCMCのアルゴリズムとしては、HMC（ハミルトニアンモンテカルロ法）の実装方法の一つであるNUTSが使われています。
WinBUGSではギブスサンプラーなどが使われていましたが、それとは異なることに注意してください。

Stanはそれ単体としては使わず、RやPythonといった別のプログラミング言語を介して使われることが多いです。
ここではR言語を介してStanを使う方法を説明します。

 

2．Stanのインストール

RからStanを使うわけですが、両者はまったく異なるソフトです。なので、Rから外部パッケージを落とすだけ、というわけにはいきません。

まずはStanをインストールします。
「Stan インストール」で検索していただければ、情報はすぐに手に入りますが、私はよく拝見させていただいている下記のサイト様を参考にしてインストールしました。

銀座で働くデータサイエンティストのブログ｜Stanで統計モデリングを学ぶ(1): まずはStanの使い方のおさらいから
http://tjo.hatenablog.com/entry/2014/01/27/235048

Qiita｜【R言語】 C++ベースで早く動く MCMC Sampler {Stan}をRから動かす ～{RStan}パッケージのセットアップ方法
http://qiita.com/HirofumiYashima/items/fee027b0cacb04d242e1

基本的には「銀座で働くデータサイエンティストのブログ」を見ながら進めて、Qiitaをたまに参照する感じがちょうどよいかと思います。

管理人がやった作業を簡単に書いておきます。
なお、OSはWindows7(64bit)、Rはバージョン3.2.2です。

※ あくまでも管理人がやった作業ですので、お使いのコンピュータの状態によっては、この通りしてもインストールできないことがあります。

まずは、Rを再インストールするところから始めました。
理由は、Rのインストール先のパス名にスペースがあると、ソフトが落ちてしまうことがあるからです。
例えば、デフォルトの「C:\Program Files」では、フォルダ名にスペースが入っているので動きません。
また、念のため、全角文字が入っていないフォルダを選んで、インストールしました。

次に、インストールした最新のRを右クリックして「管理者として実行」します。
これでパッケージをインストールする準備が整いました。

まずは、Rstanを入れる前に、そのほかのパッケージをインストールします。

# rstanを入れる準備
install.packages('inline')
install.packages('Rcpp')

ここで、いったんRを閉じます。
ここからは、Rを使わない作業に移ります。
「Rtool」と呼ばれるソフトをインストールします。
下記のリンク先からダウンロード、インストールができるはずです。

https://github.com/stan-dev/rstan/wiki/Install-Rtools-for-Windows

途中、上記サイトに張られているスクリーンショットと同じ画面が出てきたら、チェックボックスを必ず入れるようにしてください。
Rにおいて下記のコードを実行して、「Rtool」という文字が入っているのを確認できればOKです。

# Rtoolsを入れる
# https://github.com/stan-dev/rstan/wiki/Install-Rtools-for-Windows
# 確認
Sys.getenv('PATH')
system('g++ -v')

次はいよいよ、Stanのインストールです。
これは「rstan」と呼ばれるRとStanをつなげるためのパッケージをインストールすると、勝手に本体であるStanもインストールされます。
よって、ここでの作業はRでのみ行われます。

まずはRを管理者として起動します。
次に、以下のコードを実行します。

library(inline) 
library(Rcpp)

install.packages("rstan", dependencies = TRUE)

これで準備完了です。
私はこれですんなり入りましたが、万が一うまくいかなければ、例えば、パソコンのユーザー名に全角文字が入っていないか、フォルダに全角やスペースが入っていないかを確認されるとよいかと思います。

 

3．Stanを実行する流れ

Stanのインストールが無事にできたとしましょう。
RからStanを実行してベイズ推定を行うには、以下のステップを踏みます

ステップ1：Stanを使用する準備
ステップ2：統計モデルの記述
ステップ3：データの指定
ステップ4：ベイズ推定の実行
ステップ5：うまく推定されているかをチェック
ステップ6：結果の解釈

この中で、「Stanの使い方を覚えるだけ」で済むのは、ステップ1と3だけです。
ぜひソフトの使い方だけでなく、推定方法の基礎や推定結果のチェック、解釈にも注意を向けていただければと思います。

この記事では、アルゴリズムの詳細は説明しませんが、結果を解釈するのに最低限必要となる知識に関しては、なるべく記載するようにします。

 

4．今回推定する統計モデルの概要

今回は、のちに状態空間モデルをStanで推定することを考えて、ナイル川の流量データを対象とすることにします。

この記事では、まずはStanによるパラメタ推定の基礎を抑えていただくため、過程誤差の分散を0と仮定します。
よって、推定されるのは、観測誤差の分散と、常に一定の値をとる状態の値のみとなります。

軽く補足をしておきます。
状態空間モデルでは、データの変動を「見えない状態の変動」と「観測誤差」の2つに分けて考えます。
見えない状態とは、たとえば、海の中にいる魚の数といったものを想像すればよいでしょう。
「見えない状態の変動」を過程誤差と呼びます。魚の数の増減を表す部分ですね。
そして、釣りをするなどして漁獲すると、観測データが手に入ります。この時の漁師さんの腕のよしあしなどによる変動を「観測誤差」とみなして、別に推定を行います。
こうすることで、柔軟にデータをモデル化できます。

状態空間モデルと仮定誤差・観測誤差に関してもう少し詳しく知りたい方は、こちらの記事をご覧ください。

状態空間モデルに興味がない、あるいは、まずはStanによるベイズ推定の方法のみを知りたいという方は「データの平均値と分散をベイズ推定するのだ」とご理解いただいても差し支えありません。

今から、Stanを使って、ナイル川の流量の平均と分散を推定します。

 

5．ステップ1：Stanを使用する準備

Stanがインストールできていれば、以下を実行するだけでOKです。

# ライブラリの読み込み
require(rstan)

ちなみに、どれほど早くなるかはデータや状況により異なりますが、並列化演算をさせることもできるようです。

# 計算の並列化
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())

 

6．ステップ2：統計モデルの記述

次は統計モデルの記述に移ります。
ここが、データ解析において、最も重要な部分です。

データの平均値と分散を推定する場合は、以下のようなコードになります。

# モデルの作成
localLevelModel_1 <- "
  data {
    int n;
    vector[n] Nile;
  }
  parameters {
    real mu;                # 確定的レベル（データの平均値）
    real<lower=0> sigmaV;   # 観測誤差の大きさ
  }
  model {
    for(i in 1:n) {
      Nile[i] ~ normal(mu, sqrt(sigmaV));
    }
  }
"

ちょっと見づらいのですが、localLevelModel_1という変数に、ダブルクォーテーションマークで囲まれた文字列を定義しています。
ダブルクォーテーションマークを忘れないように気を付けてください。
また、かっこを除く各行ごとに、末尾にセミコロンをつける必要があります。
ちなみに、シャープ（#）記号は、コメントを表します。

モデル式は、最低でも以下の3つのブロックが必要となります。
1．データを指定するブロック
2．推定するパラメタを指定するブロック
3．データが生成されるモデルを記述するブロック

順番に説明します。

data：データを指定するブロック

  data {
    int n;
    vector[n] Nile;
  }

「int n;」で「n」という変数にサンプルサイズを指定しています。
「int」とは整数を表す接頭語です。専門用語を使うと「nという変数はint型（整数）だと宣言する」という呼び方になります。

「vector[n] Nile;」では、ナイル川の流量データは「長さnのデータですよ」と宣言しています。

宣言って、R言語ではあまり使わないのですが、「これは整数だ」とか「実数だ」とかいうのをあらかじめ宣言する必要がある点には注意してください。

parameters：推定するパラメタを指定するブロック

  parameters {
    real mu;                # 確定的レベル（データの平均値）
    real<lower=0> sigmaV;   # 観測誤差の大きさ
  }

平均と分散という2つのパラメタを推定するので、2行使っています。
「real mu;」が平均値です。「real」は実数という意味です。平均値は小数点以下の値をとることもありますので。

次の「real<lower=0> sigmaV;」が分散の大きさです。
分散は負の値をとりません。そこで「<lower=0>」と記述して「0より小さな値はとりません」と指定をしています。
この指定は、なかなか便利なのでよく使います。

model：データが生成されるモデルを記述するブロック

  model {
    for(i in 1:n) {
      Nile[i] ~ normal(mu, sqrt(sigmaV));
    }
  }

ここが最も重要です。

まず、統計モデルとはなんだったのかを思い出してください。
統計モデルとは、確率分布です。
そして、今あなたの手元にあるそのデータは、確率分布から生成されたものだとみなします。

3行目の「Nile[i] ~ normal(mu, sqrt (sigmaV));」は、以下のように解読します
ナイル川データの i 番目のデータは、平均値 mu、分散 sigmaV の正規分布に従って生成されます。

モデルを指定するとは、確率分布を指定することにほかならないのです。

2行目の「for(i in 1:n)」とは、「添え字 i を 1 から n（サンプルサイズ）まで増やして、何度も実行してください」という指定です。
ナイル川データを、1番目から最後まで順に、すべて「平均値 mu、分散 sigmaV の正規分布に従って生成されている」とみなしてくださいという指定をしていることになります。

ちなみに「sqrt」は平方根（ルート）をとってくださいという指定です。
Stanの「normal」の引数は、平均値と標準偏差なんですね。分散ではなく。そこで sqrt を入れています。これを入れなければ sigmaV が標準偏差として扱われてパラメタ推定が行われます。

モデル式と、ベイズの定理の関係

今回推定する統計モデルをベイズの定理に当てはめてみます。

ベイズの定理の基本形はこちらです。

$$f(θ|X)=\frac{f(X|θ)f(θ)}{f(X)}$$

ここで、推定するパラメタがθ、データがXです。

今回の「ナイル川流量の平均と分散を推定するモデル」の場合は、以下のようになります。

$$f(mu, sigmaV|ナイル川データ)=\frac{f(ナイル川データ|mu, sigamaV)f(mu, sigamaV)}{f(ナイル川データ)}$$

右辺の「f(ナイル川データ|mu, sigamaV)」が
modelブロックにおける「Nile[i] ~ normal(mu, sqrt (sigmaV));」に該当します。
modelブロックは、尤度関数「f(X│θ)」を指定しているということです。

尤度関数「f(X│θ)」は「パラメタがわかっているときに、データが得られる確率」を意味します。
「期待値 mu、分散 sigmaV の正規分布からデータが得られる」という統計モデルを指定してやれば、「今回のデータが得られたということは、パラメタ（muやsigmaV）はきっとこういう値をとるのだろうな」ということをStan君がベイズの定理を使って計算してくれるというイメージです。

これで、ベイズの定理に、パラメタとデータを入れてやることができました。
後は、コンピュータに任せて、パラメタ推定をしてもらうだけです。
「だけ」とはいっても、まだ作業はたくさんありますが。

 

7．ステップ3：データの指定

Stanに渡すデータをリスト形式で保持します。
もともとのデータはNileという、Rの組み込みデータです。

> # データの指定
> Nile
Time Series:
Start = 1871 
End = 1970 
Frequency = 1 
  [1] 1120 1160  963 1210 1160 1160  813 1230 1370 1140  995  935 1110  994
 [15] 1020  960 1180  799  958 1140 1100 1210 1150 1250 1260 1220 1030 1100
 [29]  774  840  874  694  940  833  701  916  692 1020 1050  969  831  726
 [43]  456  824  702 1120 1100  832  764  821  768  845  864  862  698  845
 [57]  744  796 1040  759  781  865  845  944  984  897  822 1010  771  676
 [71]  649  846  812  742  801 1040  860  874  848  890  744  749  838 1050
 [85]  918  986  797  923  975  815 1020  906  901 1170  912  746  919  718
 [99]  714  740

このままだとStanに渡せないので、以下のように整形します。

> # Stanに渡すために整形
> NileData <- list(Nile = as.numeric(Nile), n=length(Nile))
> NileData
$Nile
  [1] 1120 1160  963 1210 1160 1160  813 1230 1370 1140  995  935 1110  994
 [15] 1020  960 1180  799  958 1140 1100 1210 1150 1250 1260 1220 1030 1100
 [29]  774  840  874  694  940  833  701  916  692 1020 1050  969  831  726
 [43]  456  824  702 1120 1100  832  764  821  768  845  864  862  698  845
 [57]  744  796 1040  759  781  865  845  944  984  897  822 1010  771  676
 [71]  649  846  812  742  801 1040  860  874  848  890  744  749  838 1050
 [85]  918  986  797  923  975  815 1020  906  901 1170  912  746  919  718
 [99]  714  740

$n
[1] 100

Step2で、データとしてサンプルサイズ「n」とナイル川流量データ「Nile」を設定していたことを思い出してください。その2つをリスト形式で保管しました。
ちなみにもともとのNileデータは「ts」と呼ばれる時系列データ形式で保存されています。それをas.numericを使って、単なる数値として扱うように修正をしてあります。

 

8．ステップ4：ベイズ推定の実行

いよいよベイズ推定を実行するのですが、その前に、実行する関数とその引数の説明をしておきます。

まず、その名も「stan」という関数を使います。
これを使えば、ベイズ推定ができます。
引数はかなりたくさんあるのですが、まずは以下のものを覚えておいてください。

model_code
ステップ2で記述された統計モデルの式を指定します。
なお、これは別のファイルに保存されたものを使っても構いません。今回は、すべてRの中で記述するようにしました。

data
読んで字のごとく、データです。ステップ3で作成されたものをそのまま渡します。

iter
繰り返し回数です。
具体的には「何回乱数を発生させるのか」を指定します。
例えば「iter=1000」を指定すると、平均値というパラメタも、分散というパラメタも1000個作成されます。
その1000個のパラメタを使って、パラメタの平均値（EAP推定量）などを計算します（実際のところは、結果の計算に使われるのはこの個数よりも少なくなります）。

… …
ここからは、結果の調整をするのに使用されるパラメタに移ります。
MCMCは非常に便利なツールでして、事後分布に従うパラメタの乱数を発生させることができます。
でも、例えば1000個パラメタの乱数を生成したら、最初の数百個は、事後分布に従わない、ヘンテコな結果を返してしまいます。
また、100番目に生成された乱数と、101番目に生成された乱数がよく似た値になってしまう（生成された乱数が自己相関を持ってしまう）こともあります。これでもやはり、正しい結果は得られません。
こういった問題を解決していきます。

warmup
warmupは捨てる個数です。
捨てる対象は、作成されたパラメタです。
例えば、iter=1000でwarmup= 100だと、生成された1000個のパラメタのうち、最初の100個を捨てます。捨てられたパラメタはEAP推定量などを計算する際に使用されません。こうすれば、事後分布に従わない邪魔なシミュレーション結果を排除して、正しい結果のみを使用することができます。

thin
thinとは、「何個おきに結果を使用するか」を設定するパラメタです。
「thin=3」を指定すると、「生成された乱数を3つおきに使用する」ことになります。
iter=6でthin=2だと、使われるデータは１，３，５番目のシミュレーション結果だけです。
こうすれば、生成された乱数の自己相関をある程度緩和してやることができます。

chains
chainsは「iter回数行うシミュレーション」を何回行うかを指定します。chainsは3を指定することが多いです。
例えば「iter=1000」で「chains=3」だと、1000回乱数を発生させるという行為を3回繰り返します。
なんで同じことを何度もするかというと、計算された結果を信用してもよいかどうかチェックしたいからです。
何度も言いますが、MCMCは乱数発生アルゴリズムです。
ランダムな値を発生させるため、計算するたびに、異なる結果が出てきます。
それが「ちょっと違うだけ」ならいいのですが、計算するたびにパラメタのEAP推定量が100になったり1億になったりするというのでは問題です。
そこで同じ計算を何度もやり直して「似たような結果になるかどうか」を確認するのです。
その結果は、後で紹介しますが「Rhat」という指標で現れます。
Rhatが1.1以下であれば「シミュレーションをやり直してもちゃんと似たような結果になっている」言い換えると「パラメタが収束した」とみなすことができます。
ただし、Rhatは参考程度にしかなりません。
後で見るように、必ず結果をプロットして確認するようにしてください。

長らくお待たせいたしました。
データの平均と分散を推定する際のコードは下記のとおりです。

実はというと、下記のコードを実行すると、ちょっとよくない結果が出てきます。
結果のどこがまずくて、どのように修正すればよいかを説明するために、あえてよくない引数を指定しています。

# 乱数の種
set.seed(1)

# 確定的モデル
NileModel_1 <- stan(
  model_code = localLevelModel_1,
  data=NileData,
  iter=1100,
  warmup=100,
  thin=1,
  chains=3
)

set.seed(1)は、乱数の種です。
乱数発生アルゴリズムを使ってパラメタ推定をすると、推定結果が毎回変わります。
これは仕方がないことなのですが、サイトをご覧になっている方が計算結果の答え合わせができなくなってしまいます。
ということで、出てくる乱数を固定するために「set.seed(1)」を指定しました。
これはstanの引数として指定することもできます。

メインはそのあとです。
モデル式にはステップ2で作成された「localLevelModel_1」を入れます。
データにはステップ3で作成された「NileData」を入れます。
繰り返し回数は1100回。
捨てる個数は100回です。
thinによる間引きは行わないようにしたのでthin=1にしておきました。1つおきにデータを使用するということはすなわち、全部のデータを使うということです。
よって、結果に出力されるのは101個目のシミュレーション結果からとなります。
このシミュレーションを3回繰り返しました(chains=3)。

初めてこのモデルを組む時は、計算には数分かかることもあります。しかし、2回目以降は短い時間で計算が終わります。
これはStanの優秀なところです。

 

9．ステップ5：うまく推定されているかをチェック

結果を確認しましょう（画面が狭いので、折り返しています。）。

> # 結果の確認
> # 推定されたパラメタ
> NileModel_1
Inference for Stan model: e1c2b5e53ca964864054985696499665.
3 chains, each with iter=1100; warmup=100; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=3000.

           mean se_mean       sd     2.5%      25%      50%      75%    97.5%
mu       912.78    3.87    40.07   850.94   904.68   917.33   929.72   949.53
sigmaV 31150.22 1470.50 13904.43 22590.69 26803.46 29351.03 32289.62 42111.20
lp__    -554.42    0.91     8.22  -560.35  -553.77  -553.09  -552.66  -552.39
       n_eff Rhat
mu       107 1.02
sigmaV    89 1.02
lp__      81 1.03

Samples were drawn using NUTS(diag_e) at Thu Dec 03 22:35:52 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

NileModel_1という名前で保存された推定結果を直接打ち込んで実行することで、たくさん乱数が生成されたパラメタ「mu」と「sigmaV」の結果が出てきます。
たくさん生成された「mu」の結果などを使って、「mean:パラメタの期待値（EAP推定量）」や95%区間などを求めています。
Rhatを見ると、1.1以下なので問題無いようにも見えます。

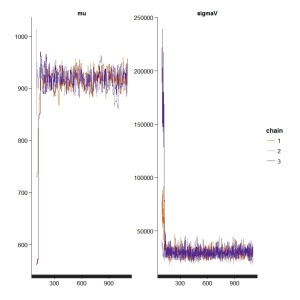
しかし、シミュレーション結果をプロットすると、おかしな点に気付きます。

グラフの最初のほうだけ、変なことになっていますね。
これは、生成された乱数がまだ収束できていないことが原因です。warmupが短すぎたようです。
そこで、warmupとiterを増やして、再度実行します。

set.seed(1)

# warmup期間が短すぎたようなので、増やす
NileModel_2 <- stan(
  model_code = localLevelModel_1,
  data=NileData,
  iter=1500,
  warmup=500,
  thin=1,
  chains=3
)

繰り返し数を1500回。捨てる個数を最初の500個としました。

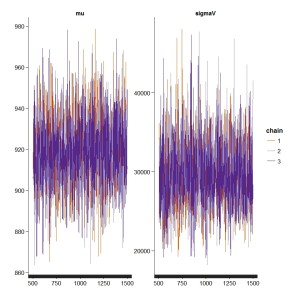
結果はこちら。Rhatが1ピッタリになっています。

> # 推定されたパラメタ
> NileModel_2
Inference for Stan model: e1c2b5e53ca964864054985696499665.
3 chains, each with iter=1500; warmup=500; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=3000.

           mean se_mean      sd     2.5%      25%      50%      75%    97.5%
mu       919.08    0.45   17.34   885.30   907.34   919.22   930.12   954.39
sigmaV 29666.36  110.54 4387.86 21973.19 26583.46 29299.84 32476.50 39109.00
lp__    -553.40    0.03    1.00  -556.15  -553.78  -553.11  -552.66  -552.38
       n_eff Rhat
mu      1502    1
sigmaV  1576    1
lp__     952    1

Samples were drawn using NUTS(diag_e) at Thu Dec 03 22:45:42 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

トレースプロットも問題ありません。

# 計算の過程を図示
traceplot(NileModel_2)

これでようやくパラメタ推定が出来上がりました。
今回はiterとwarmupを修正しましたが、thinも合わせて修正したほうが良い時もあります。ここは試行錯誤をするしかありません。
少し面倒ですが、必要な作業なので、推定結果はその都度確認されたほうがよろしいかと思います。複雑なモデルが一発で推定できることはほとんどないです。

この記事のように早く計算が終わればよいのですが、複雑なモデルを組むと計算に時間がかかります。そういう時に限ってパラメタが収束しないのは、私の普段の行いが悪いからでしょうか。
それは冗談ですが、仕組みが大体わかって、コードも書くことができるとなっても、実際のところ、計算に相当の時間がかかってしまうこともあります。複雑なモデルを組む際は、余裕をもって取り組まれたほうがいいかもしれません（あまり試したことはないのですがStanはWinBUGSという別のMCMCするソフトよりも収束がよいとのことです。昔WinBUGS使って論文を書いた時は、大変でした）。

 

10．ステップ6：結果の解釈

最後に、推定されたパラメタの解釈に移ります。
とはいえ、今回は平均と分散を推定しただけなので、やることはあまりありませんね。

例えば、パラメタmuの行を見てください。
mean列に919.08とあります。これがパラメタmuのEAP推定量です。言い換えると「たくさん生成されたパラメタmuの平均値」です。
あとは、「たくさん生成されたパラメタmuの標準偏差」や95％区間などが載っています。
lp__は対数確率密度と呼ばれ、推定されたパラメタとはちょっと違うので気を付けてください。
パラメタの行以外は、主にどのような計算をしたかを説明しているだけですので、最初のうちはあまり気にしなくても問題ないかと思われます。

ちなみに、パラメタの95%区間が出ていますが、これはそのまま「パラメタmuが885.30から954.39の間にある確率が95%だ」と解釈していただいて問題ありません。
頻度主義の場合は難しかったのですが、ベイズの場合は気にしなくてもよいです。

これでベイズ推定完了です。
お疲れ様でした。

 

11．Stanの補足：事前分布について

ベイズの定理を使う場合、本来ならば事前確率を指定しなくてはなりません。
先ほどのコードですと、すべて事前確率（正確には事前確率分布）を一切指定しませんでした。この場合は、一様分布の事前確率分布が勝手に指定されます。査読者によっては事前分布を何にするかを気にする人もいるので、その場合は適宜修正してください。私は特殊な事情がなければ、一様分布でいいと思います。とはいえ、ここを変えると、収束がよくなることもありました（WinBUGSの場合ですが）。

ちなみに、事前分布を指定する場合は、ステップ2のモデル式を作成する段階で修正をかけます。
modelブロックの中に例えば「mu ~ normal(0, 100000);」と入れておくと、muの事前確率分布が平均0で標準偏差100000の正規分布とみなして計算されます。

 

参考文献

基礎からのベイズ統計学: ハミルトニアンモンテカルロ法による実践的入門   何度も紹介していますが、ベイズ推定について書かれた良書です。 巻末の付録にStanの使い方も書かれています。

岩波データサイエンス Vol.1 特集「ベイズ推論とMCMCのフリーソフト」   こちらも何度も紹介している本です。 ソフトの使い方に関しては、こちらのほうが詳しいです。 Stan以外にも、MCMCをするソフトはたくさんあります。 色々なソフトを使ってみたいという方にもおすすめです。 （もちろんStanも1章割いて載っていますよ）

データ解析のための統計モデリング入門―― 一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)   統計モデルとベイズ推定、両方一気に学びたい方にお勧めです。 大変読みやすい本なのでお勧めです。 なお、ソフトはWinBUGSという別のものが使われているので注意してください。

平均・分散から始める一般化線形モデル入門   管理人の書いた本です。 ベイズ推定に関しては載っていません。 代わりに、統計モデルの基礎をかなり丁寧に書きました。 統計モデルや尤度について勉強したい方はどうぞ。

リンク

この記事はベイズ推定を応用して状態空間モデルを推定する一連の記事の一つです。
記事の一覧とそのリンクは以下の通りです。
・ベイズ統計学基礎
・ベイズと統計モデルの関係
・ベイズとMCMCと統計モデルの関係
・Stanによるベイズ推定の基礎
・Stanで推定するローカルレベルモデル

スポンサードリンク