TMBを活用して、状態空間モデルをラプラス近似により高速に推定する
カルマンフィルタでもなく、ベイズ推論でもない。ラプラス近似を利用した最尤法で状態と分散などのパラメータをまとめて推定してしまう方法について解説します。
なお、本記事は別の記事で書評を書かせていただいた「Rで学ぶ個体群生態学と統計モデリング」の内容を参考にしています。なお、こちらの書籍よりもずっと簡単なモデルをこの記事では推定しています。
コードについてはGitHubからダウンロードできます。
目次
- 状態空間モデルの推定方法について
- ローカルレベルモデルの推定
- 分析の準備
- KFASを用いた状態空間モデルの推定
- TMBを用いた状態空間モデルの推定
- 二項分布のDGLMの推定
- ランダム効果付きポアソンDGLMの推定
1.状態空間モデルの推定方法について
状態空間モデルは便利ですが、例えばベイズ推論とMCMCの組み合わせで推定を行う場合、推定にはしばしば豊富なコンピューター資源と長い時間を要します。
状態空間モデルを推定する方法としては、以前逐次推定系と、一括推定系の2つに分かれると述べました。最近はいろいろな教科書でも似たような記述が見られており、ある程度無難な分類基準になっていると思います。
状態空間モデルを高速に推定する場合、普通は逐次推定を利用します。カルマンフィルタと最尤法の組み合わせは特に、きわめて高速なモデルの推定を可能とします。しかし、この方法は、線形ガウス状態空間モデルにしか利用できません。
非線形、非ガウス型状態空間モデルを推定する場合は、特にパラメータ推定まで行おうと思った場合にはベイズ推論とMCMCの組み合わせを利用することが多かったです。
ところで別の記事で書評を書かせていただいた「Rで学ぶ個体群生態学と統計モデリング」では、ラプラス近似を用いて状態空間モデルを推定する方法が記載されていました。
正直なところ、ラプラス近似は、私の頭の中ではかなりマイナーな技術という扱いで、GLMMを推定するときにそんなことしてたなーくらいの印象しかありませんでした。しかし、ラプラス近似はランダム効果を持つモデルを推定するために一般的に利用できる手法であり、状態空間モデルの推定にも利用できます。
また、同書籍に解説のあったTMB(Template Model Builder)が非常に使いやすく、文字通り爆速でモデルの推定を可能としています。爆速に状態空間モデルが推定できるので、本ブログでは状態空間モデルをラプラス近似で推定する事例をいくつか紹介しようと思います。
なお「Rで学ぶ個体群生態学と統計モデリング」を読んで初めて使い方を知ったライブラリですので、まだ当方も手探りなところがあります。技術的な詳細は、書籍を参照してください。生態学に関係のないデータサイエンティストでも有益な書籍だと思います。
状態空間モデルの基本的な事項については説明を略します。詳細はこちらの記事を参照してください。
2.ローカルレベルモデルの推定
分析の準備
まずはライブラリを読み込みます。
library(tidyverse) library(KFAS) library(TMB) library(ggfortify) # autoplotのために使用 library(gridExtra) # 複数のグラフをまとめて表示させる
ローカルレベルモデルに従うデータをシミュレーションで生成します。
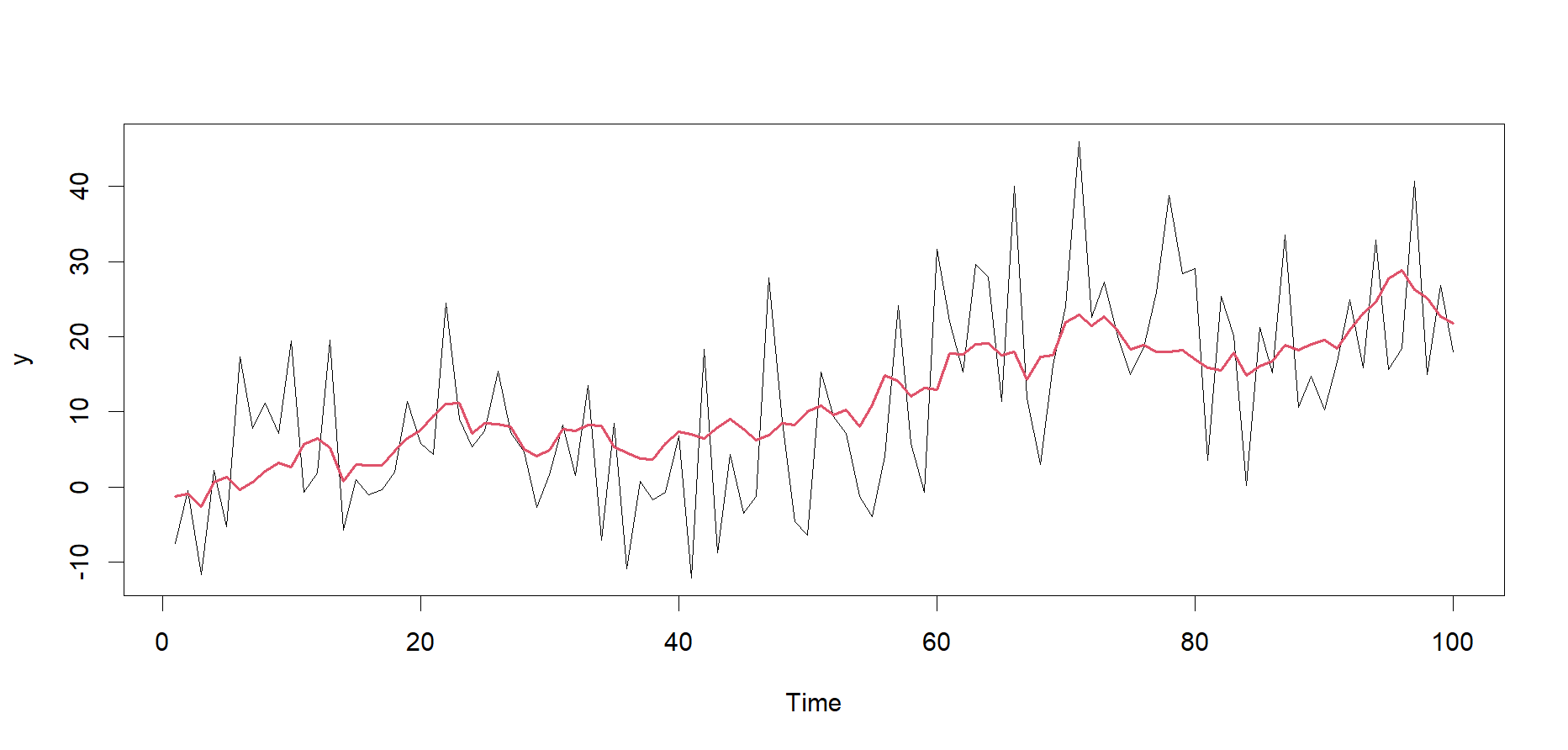
# 乱数の種 set.seed(1) # サンプルサイズ n <- 100 # ローカルレベルモデルに従うシミュレーションデータ mu <- rnorm(n = n, mean = 0, sd = 2) |> cumsum() |> ts() y <- mu + rnorm(n = n, mean = 0, sd = 10) |> ts() # 可視化 plot(y, type = "l") lines(mu, col = 2, lwd = 2)
KFASを用いた状態空間モデルの推定
まずは比較のため、本ブログでも良く利用しているKFASを使って、ローカルレベルモデルを推定してみます。
# Step1:モデルの構造を決める
build_kfas <- SSModel(
H = NA,
y ~ SSMtrend(degree = 1, Q = NA)
)
# Step2:パラメタ推定
fit_kfas <- fitSSM(build_kfas, inits = c(0, 0))
# Step3、4:フィルタリング・スムージング
result_kfas <- KFS(
fit_kfas$model,
filtering = c("state", "mean"),
smoothing = c("state", "mean")
)
推定された観測誤差・過程誤差の標準偏差を確認します。過程誤差は2、観測誤差は10が正解なので、割と良い推定結果になっているようです。
> # 観測誤差の標準偏差
> fit_kfas$model$H |> sqrt()
, , 1
[,1]
[1,] 9.667595
>
> # 過程誤差の標準偏差
> fit_kfas$model$Q |> sqrt()
, , 1
[,1]
[1,] 1.836924
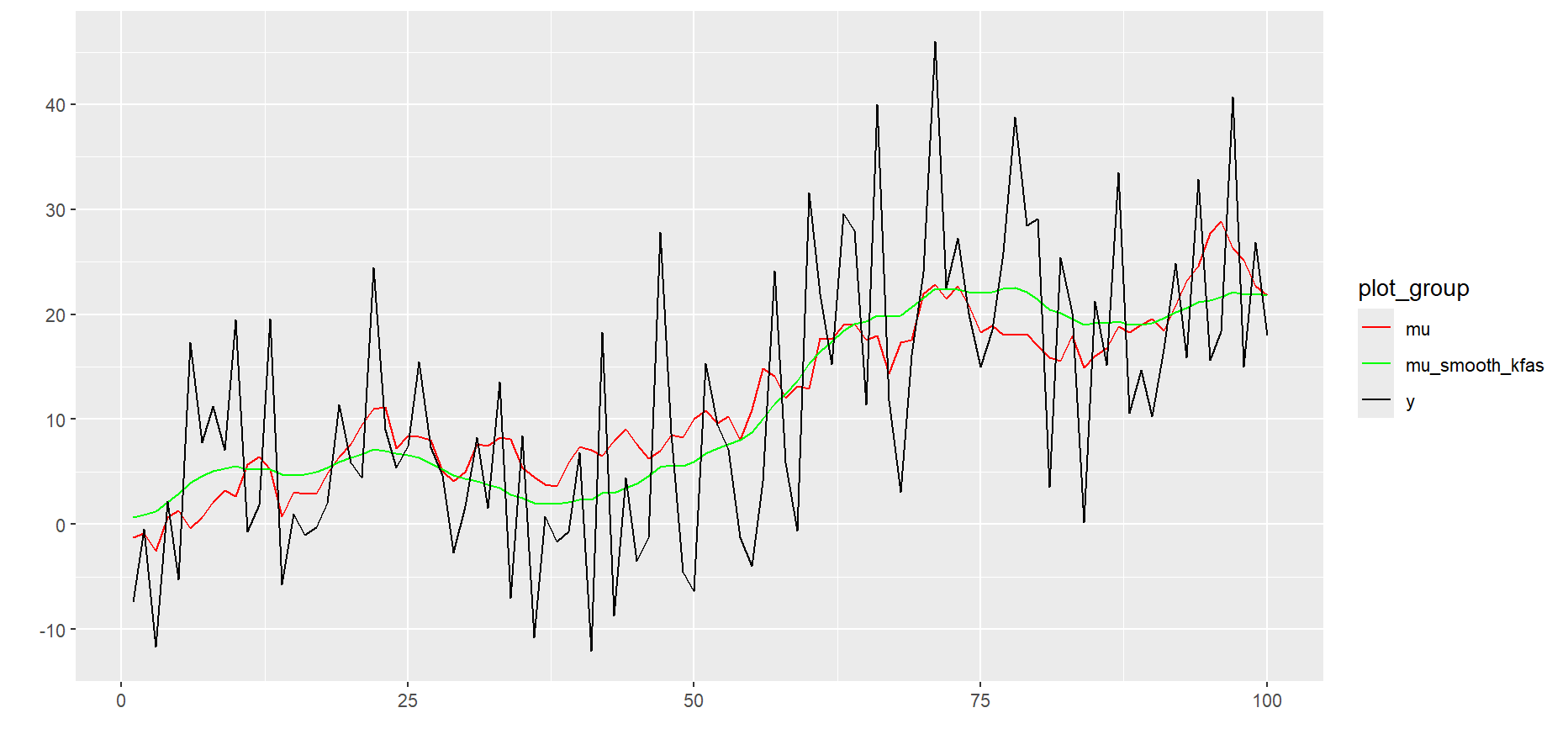
推定された状態を可視化します。まずはts.union関数を使って、観測値・シミュレーションで生成された正しい状態・状態空間モデルで推定された状態の3つをまとめます。ts型のデータをくっつける際はts.union関数が便利です。そしてautoplot関数を使ってグラフを描きます。グラフを見る限り、正しい状態muと、推定されたmu_smooth_kfasはかなり近い値となっているようです。
# 可視化
plot_data <-
ts.union(
y, # 観測値
mu, # 正しい状態
mu_smooth_kfas # 状態推定値
)
autoplot(plot_data, facets = FALSE)
TMBを用いた状態空間モデルの推定
今回のメインテーマである、TMBを使ってみます。
なお、このコードを作成するにおいて、「Rで学ぶ個体群生態学と統計モデリング」はもちろんですが、TMBによる状態空間モデル(ローカルレベルモデル)|伊東生態統計研究室も参考にさせていただきました。
「Rで学ぶ個体群生態学と統計モデリング」では平均値を推定する事例など、初歩的なところから解説されています。
TMBを一言でいうと、「統計モデルを推定するのが主な用途である、自動微分を行うライブラリ」になると思います。微分は最適化(関数の最小・最大を求める)際によく使います。最尤法ではモデルの対数尤度を最大にする計算を行います。そのためTMBを使うと、非常に高速に最尤法によるパラメータ推定を実行することができます。ついでにラプラス近似を利用して尤度を簡単に計算できる機能が付いているので、複雑な階層モデルでも比較的簡単に推定できます。
私の理解では、TMBができることは以下の通りです(他の機能もあると思うけど)。
1.確率分布を指定すれば(確率密度関数を自分で計算しなくても)尤度が計算できる
2.ラプラス近似を使って、複雑なモデルでも尤度を計算できる
3.自動微分ができる
この辺の機能をうまく使って、最尤法に基づき、爆速で状態空間モデルを推定していきましょう。
(最適化計算によってMAP推定量が得られるので、ベイズ推論によるモデルの推定も一応できるようです。)
TMBを利用する場合には、cppファイルというRファイルとは別の「モデルの構造を記述したファイル」を用意する必要があります。
RStudioにおいて、File→New File→C++ Fileを選択するとcppファイルを作ることができます。
書籍ではRファイル内で完結させていましたが、ファイルを細かく分けるのが当方の趣味なので分けておきました。
ローカルレベルモデルのモデルの構造式を載せておきます。この構造式の通りにプログラムを書いていきます。なおtは時点を表します。t-1は1時点前を表します。μ_tが状態、y_tが観測値です。s_w^2が過程誤差の分散であり、s_v^2が観測誤差の分散です。1行目を状態方程式、2行目を観測方程式と呼びます。
$$
\begin{align}
\mu_t &\sim \text{Normal}(\mu_{t-1}, \sigma_w^2) \\
y_t &\sim \text{Normal}(\mu_t, \sigma_v^2)
\end{align}
$$
今回は以下のようなコードを「ssm1.cpp」という名前で保存します。
// ローカルレベルモデル #includetemplate Type objective_function ::operator() () { // DATA // DATA_VECTOR(Y); // 観測値 // PARAMETER // PARAMETER_VECTOR(mu); // 状態 PARAMETER(log_s_w); // 過程誤差の標準偏差の対数 PARAMETER(log_s_v); // 観測誤差の標準偏差の対数 PARAMETER(m0); // 状態の初期値 // PARAMETER TRANSFORMATION // Type s_w = exp(log_s_w); Type s_v = exp(log_s_v); // Main int T = Y.size(); // サンプルサイズ Type nll = 0.0; // 負の対数尤度 // 状態の初期値から、1時点目の状態を得る nll -= dnorm(mu(0), m0, s_w, true); // 状態方程式に従い、状態が遷移 for (int t = 1; t < T; t++) { nll -= dnorm(mu(t), mu(t - 1), s_w, true); } // 観測方程式に従い、観測値が得られる for (int t = 0; t < T; t++) { nll -= dnorm(Y(t), mu(t), s_v, true); } return nll; }
詳細な文法については「Rで学ぶ個体群生態学と統計モデリング」を参照してください(私も勉強中なので詳しくないです。ごめんなさい)。
//はコメントの記号です。
#include とかType objective_function::operator() ()とかは、約束事と思って常につけておいて良いと思います。
DATA_VECTORという関数で、Rから受け取る観測値を設定します。
PARAMETER_VECTORやPARAMETERという関数で、推定すべきパラメータを設定します。標準偏差の値は負になることがないので、あとでexp関数を適用しています。数値の「型」を設定する必要があることに注意が必要です。intが整数型であり、小数点以下を取る可能性があればTypeを使います。
nllという変数名は「Rで学ぶ個体群生態学と統計モデリング」に合わせていますが、変数名は何でもいいそうです。なお、Negative log likelihoodの略を意図してnllとなっています。
dnorm関数は正規分布の確率密度関数です。末尾にtrueと入れることで対数確率密度を出力してくれます。普通の尤度なら掛け算で値が変わりますが、対数を取ることで掛け算が足し算に代わります。そのため、dnorm関数の結果をいろいろ足し合わせることで、対数尤度を求めることができます。なお、本来は対数尤度を最大にするのですが、後ほど「最小化」の計算を行うため、対数尤度の正負を逆にし、対数尤度をどんどん引いていくことでnllを得ています。-=という演算子は「元のnllから、右辺の値を差し引く」という意味です。
今回はデータが得られる前の0時点目の状態推定値をm0という名前のパラメータとして扱っています。私が以前ブログで「左端」と書いていたところです。KFASライブラリだと散漫初期化を使ってくれるので意識する必要はないのですが、今回は明示的に推定しました。ここはいろいろな指定の方法がありそうです。
1時点目以降の状態は、すべて前の時点の状態を平均値として持つ正規分布に従うと想定しています。
記法は何となくStanに似ているような感じがします(特に対数密度加算文の書き方と似ています)。まずは利用するデータを指定し、推定するパラメータを指定、必要に応じてパラメータを変換し、最後にMainと書かれたところ以降でモデルの構造を記述します。
モデルの構造を記述することで、コンピューター上でモデルの尤度(厳密には負の対数尤度)を計算する計算式を自動で求めてくれます。これをするために、まずコンパイルというファイルの変換作業を行い、その結果を読み込む(load)ことにします。
# コンパイル
TMB::compile("ssm1.cpp")
# モデルのロード
dyn.load(dynlib("ssm1"))
パラメータの推定を実施します。先にも書いたようにTMBはあくまでも微分してくれるだけのライブラリです。そのため、最適化は別途行う必要があります。
コンパイルだのなんだのをしてくれたので、モデルの負の対数尤度とそれを微分した結果をいつでも得ることができるようになっています。それを利用して最適化を行います。
# パラメータ推定の実施 dat <- list(Y = c(y)) pars <- list(mu = rep(0, length(y)), m0 = 0, log_s_w = 0, log_s_v = 0) obj <- MakeADFun(dat, pars, random = "mu", DLL = "ssm1", silent = TRUE) opt <- nlminb(obj$par, obj$fn, obj$gr)
分析対象となるデータと、推定すべきパラメータの一覧およびその初期値を入れます。
パラメータは試行錯誤的に求めます。そのため「試行錯誤の最初の1回目」で指定する値をparsという名前で指定しています。 MakeADFun関数を使って、負の対数尤度を計算する関数、およびそれを自動微分した結果を得ます。random = "mu"と指定することで、mu全体をラプラス近似で周辺化したうえで尤度を計算してくれるようです。GLMMにおけるランダム効果や、SSMにおける状態の推定値などは基本的にrandomという引数に指定しておくことになるようです。
ssm1.cppファイルで設定されたデータおよびパラメータの名前が一致しない場合や、過不足がある場合は、エラーになります。 nlminbはTMBと関係のない、R標準搭載の最適化関数です。書籍を参考にしてこの関数を使っています。自動微分した結果をこの最適化関数に渡してあげることで、非常に早く最適化の計算を行うことができます。 推定結果は以下のようになりました。
> # 推定結果
> opt
$par
log_s_w log_s_v m0
0.5538800 2.2686874 0.8457756
$objective
[1] 377.4467
$convergence
[1] 0
$iterations
[1] 18
$evaluations
function gradient
19 19
$message
[1] "relative convergence (4)"
パラメータが見づらいので、EXPを取って、標準偏差と解釈できるようにします。正しいパラメータとほぼ同じになりました。
> # 推定された標準偏差 > opt$par[1:2] |> exp() log_s_w log_s_v 1.739991 9.666704
なお、nlminbの結果であるところのoptはあくまでも最適化を行った結果にすぎません。nlminbの結果得られたパラメータなどは、MakeADFun関数の出力であるobj内にも格納されています。obj内にあるRの環境内にいろんな結果が保存されています。例えば以下のようにすることで、推定されたパラメータの一覧を取得できます。
> obj$env$parList() $mu [1] 0.8457735 1.1147628 1.4349179 2.1795383 2.9230430 ・・・中略 [91] 19.6932605 20.2151451 20.5858438 21.1095058 21.2516064 $log_s_w [1] 0.55388 $log_s_v [1] 2.268687 $m0 [1] 0.8457756 attr(,"check.passed") [1] TRUE
書籍中で紹介されていたsdreport関数を使うことで、標準誤差を含めて推定結果を確認できます(結果は省略)。
# 推定されたパラメータの一覧(SE付き) sdrep <- sdreport(obj) summary(sdrep)
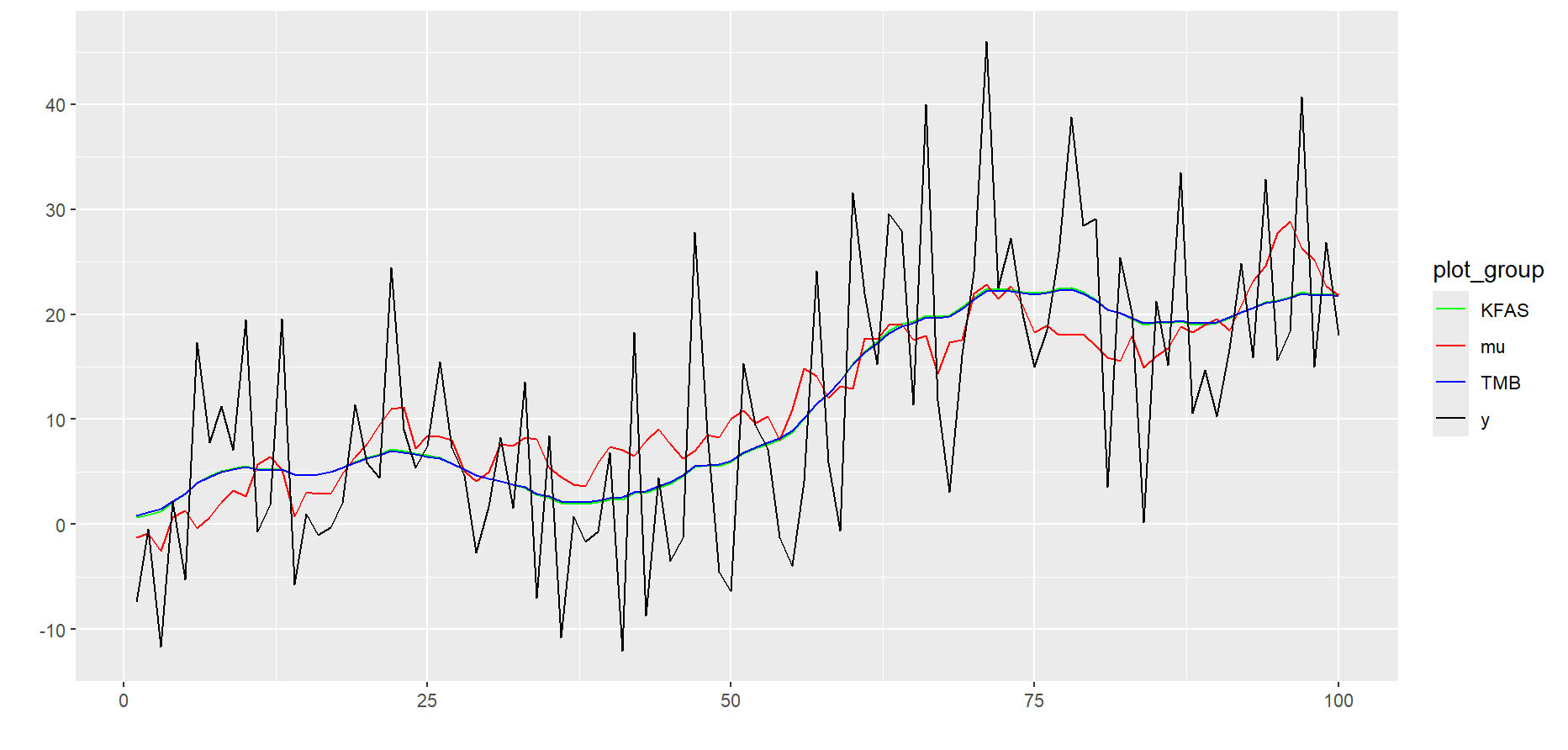
推定された状態を可視化します。KFASとTMBの結果はほぼ一致しました。
# 可視化
plot_data <-
ts.union(
y, # 観測値
mu, # 正しい状態
mu_smooth_kfas, # 状態推定値(KFAS)
obj$env$parList()$mu # 状態推定値(TMB)
)
colnames(plot_data) <- c("y", "mu", "KFAS", "TMB")
autoplot(plot_data, facets = FALSE) +
scale_colour_manual(values = c("green", "red", "blue", "black"))
3.二項分布のDGLMの推定
カルマンフィルタで対数尤度を計算できる程度のモデルならば、カルマンフィルタを使ったほうが良いです。ラプラス近似は近似ですが、カルマンフィルタはちゃんと真面目に対数尤度を計算してくれているはずです。
ここではカルマンフィルタを利用できない、二項分布に従うデータに対して状態空間モデルを適用してみようと思います。この場合は、重点サンプリングや粒子フィルタ、あるいはベイズ推論などを使うことになりがちですが、ラプラス近似を使って高速にモデルを推定できるか試してみます。
まずはシミュレーションでデータを生成します。
以下のモデル式に従います。
$$
\begin{align}
\mu_t &\sim \text{Normal}(\mu_{t-1}, s_w^2) \\
y_t &\sim \text{Binom}\left(1, \frac{1}{1 + \exp(-\mu_t)}\right)
\end{align}
$$
ランダムウォーク的に変化する状態μ_tがあり、そのロジスティック変換をしたものが、成功確率となります。その成功確率を持つ試行回数1の二項分布(ベルヌーイ分布)に従って観測値y_tが得られる形式になっています。
# 乱数の種
set.seed(1)
# 逆ロジット
logistic <- function(x) {
1 / (1 + exp(-x))
}
# サンプルサイズ
n <- 100
# シミュレーションデータ
mu <- -2 + rnorm(n = n, mean = 0, sd = 0.4) |> cumsum() |> ts()
y <- numeric(n)
for (t in 1:n) {
y[t] <- rbinom(n = 1, size = 1, prob = logistic(mu[t]))
}
# 可視化
plot(y)
lines(logistic(mu), col = 2, lwd = 2)
モデルを推定します。まずはcppファイルを作ります。「ssm2.cpp」というファイル名にしました。
// 二項分布のDGLM #includetemplate Type objective_function ::operator() () { // DATA // DATA_VECTOR(Y); // 観測値 // PARAMETER // PARAMETER_VECTOR(mu); // 状態 PARAMETER(log_s_w); // 過程誤差の標準偏差の対数 PARAMETER(m0); // 状態の初期値 // PARAMETER TRANSFORMATION // Type s_w = exp(log_s_w); vector p = 1 / (1 + exp(-mu)); // muをロジスティック変換して、成功確率とみなす Type size = 1.0; // Main int T = Y.size(); // サンプルサイズ Type nll = 0.0; // 負の対数尤度 // 状態の初期値から、1時点目の状態を得る nll -= dnorm(mu(0), m0, s_w, true); // 状態方程式に従い、状態が遷移 for (int t = 1; t < T; t++) { nll -= dnorm(mu(t), mu(t - 1), s_w, true); } // 観測方程式に従い、観測値が得られる for (int t = 0; t < T; t++) { nll -= dbinom(Y(t), size, p(t), true); } ADREPORT(p); return nll; }
ローカルレベルモデルとだいたい同じですが、成功確率pはmuをロジスティック変換した結果であること、観測値Yは二項分布に従うことが変更点となります。
また成功確率pはパラメータ扱いではないですが、非常に興味のある値なので、ADREPORT関数を使って、推定結果をレポートしてもらいました。
推定します。
# コンパイル
TMB::compile("ssm2.cpp")
# モデルのロード
dyn.load(dynlib("ssm2"))
# パラメータ推定の実施
dat <- list(Y = c(y))
pars <- list(mu = rep(0, length(y)), m0 = 0, log_s_w = 0)
obj <- MakeADFun(dat, pars, random = "mu", DLL = "ssm2", silent = TRUE)
opt <- nlminb(obj$par, obj$fn, obj$gr)
推定結果です。だいたいシミュレーションの想定と一致しました。
> # 推定結果
> opt
$par
log_s_w m0
-0.6041617 -2.5853611
$objective
[1] 49.53668
$convergence
[1] 0
$iterations
[1] 8
$evaluations
function gradient
9 9
$message
[1] "relative convergence (4)"
>
> # 推定された標準偏差
> opt$par[1] |> exp()
log_s_w
0.5465324
結果は略しますが、以下のようにして、標準誤差付きで、いろんな推定結果を確認できます。
# 推定された状態 sdrep <- sdreport(obj) summary(sdrep) summary(sdrep, select = "random")
なお、パラメータではなく、ADREPORTで追加された変数についてはsdrepの結果を介して取得する必要があるようです。
> summary(sdrep, select = "report")
Estimate Std. Error
p 0.07179246 0.09774404
p 0.07501104 0.09537925
・・・中略・・・
p 0.80076240 0.16787727
p 0.76196261 0.21169309
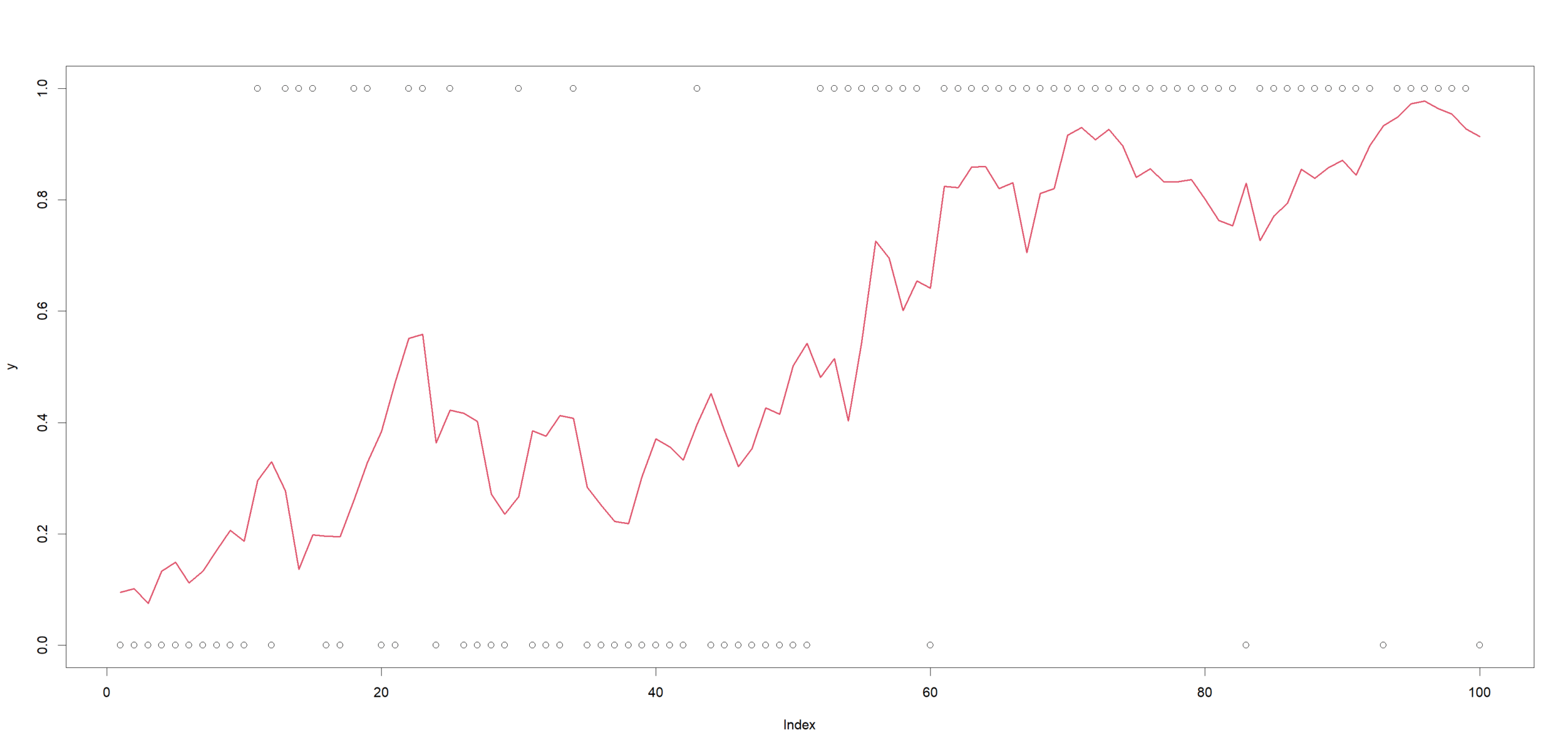
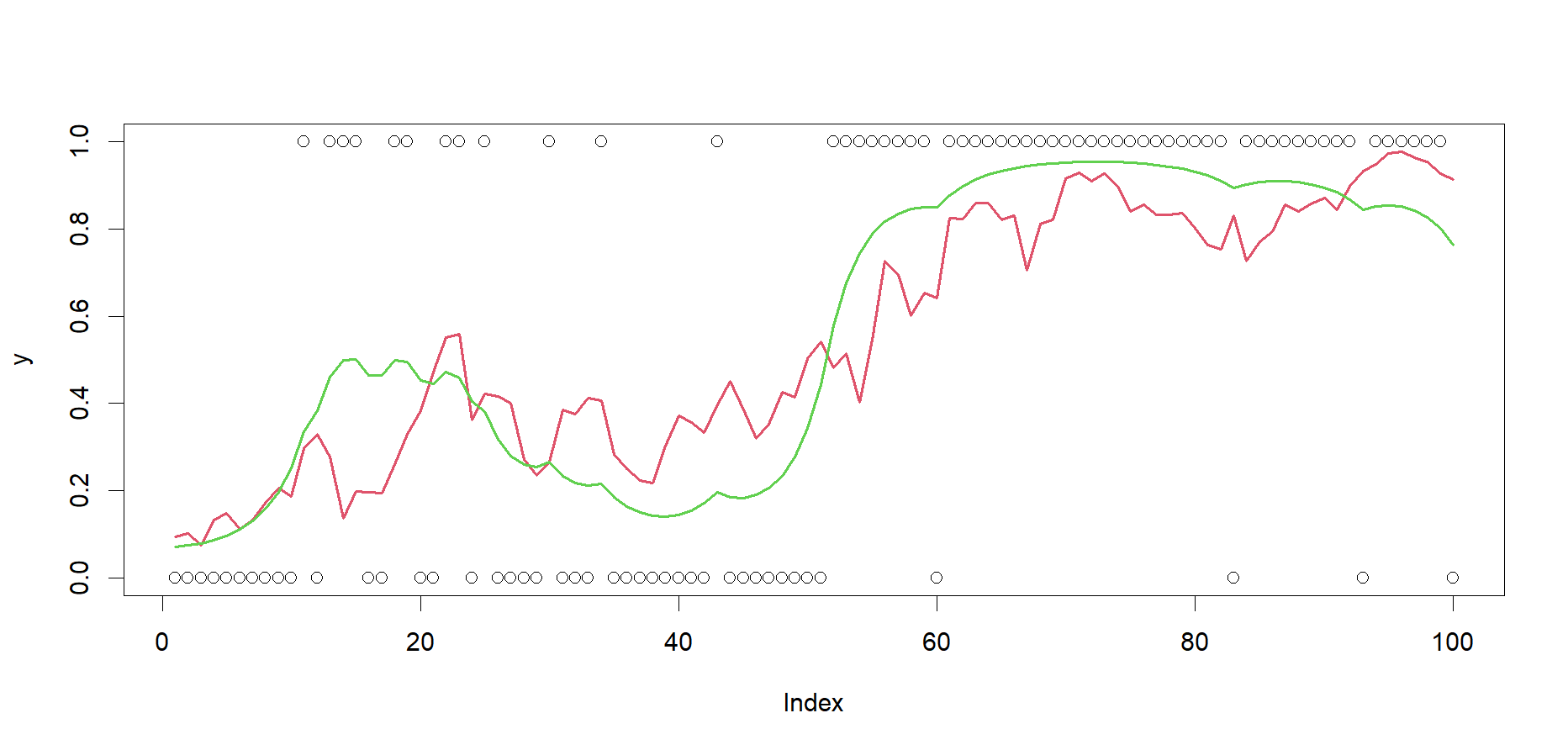
推定された成功確率の時系列推移を可視化します。緑色が推定値ですが、シミュレーションの想定と近い値になりました。
# 可視化 plot(y) lines(logistic(mu), col = 2, lwd = 2) summary(sdrep, select = "report")[, 1] |> ts() |> lines(col = 3, lwd = 2)
4.ランダム効果付きポアソンDGLMの推定
続いてポアソン分布に従うDGLMを推定します。このとき、過分散があることを想定し、以下のようなモデル式とします。観測値yを、生き物の個体数などと考える際に、観測誤差を考慮した個体数モデルとして解釈できます。
$$
\begin{align}
\mu_t &\sim \text{Normal}(\mu_{t-1}, s_w^2) \\
r_t &\sim \text{Normal}(0, s_r^2) \\
y_t &\sim \text{Poiss}(\exp(\mu_t + r_t))
\end{align}
$$
シミュレーションデータを作ります。
# 乱数の種
set.seed(1)
# サンプルサイズ
n <- 100
# シミュレーションデータ
mu <- -2 + rnorm(n = n, mean = 0, sd = 0.4) |> cumsum() |> ts()
r <- rnorm(n = n, mean = 0, sd = 0.5)
y <- numeric(n)
for (t in 1:n) {
y[t] <- rpois(n = 1, lambda = exp(mu[t] + r[t]))
}
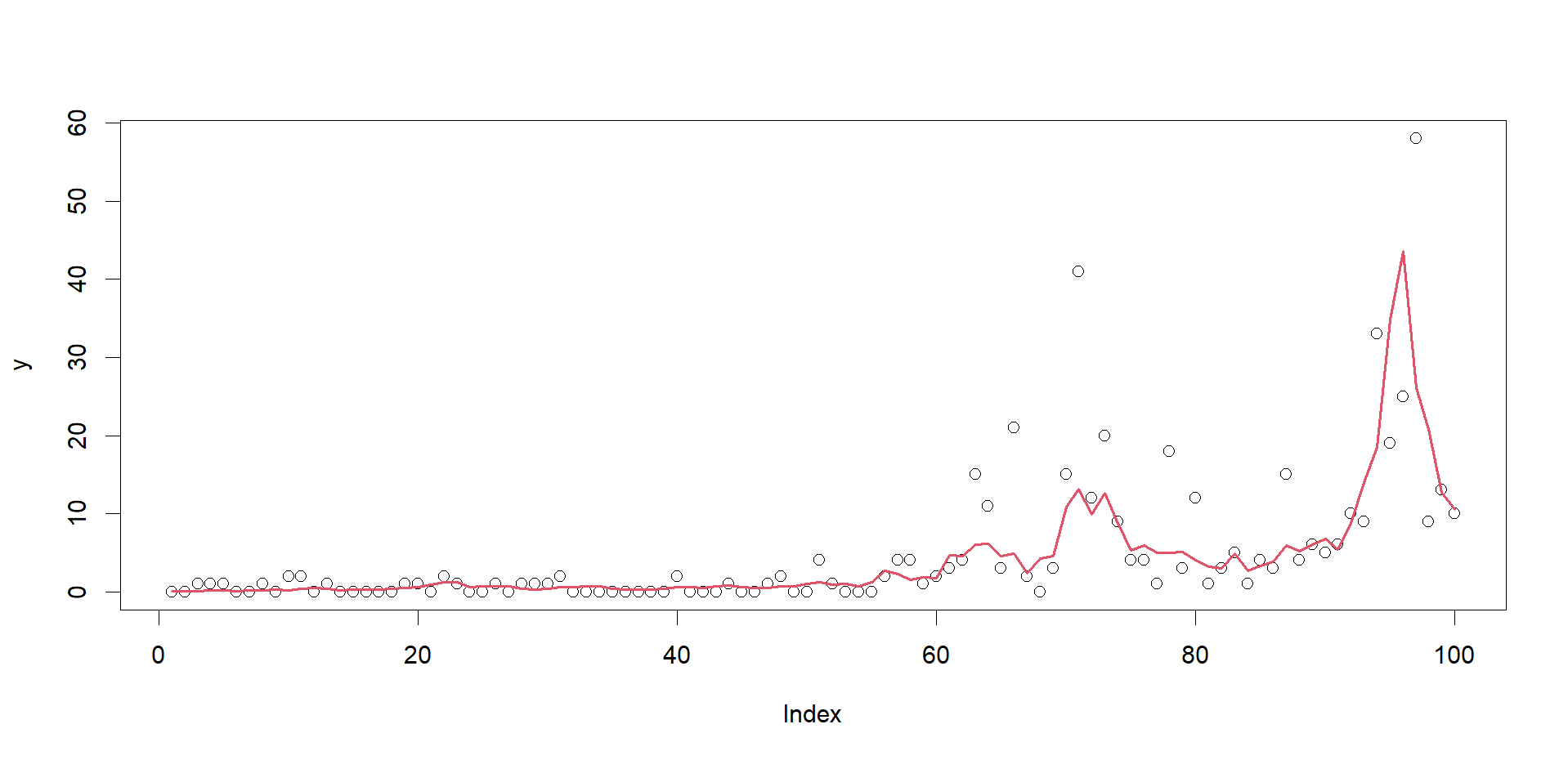
# 可視化
plot(y)
lines(exp(mu), col = 2, lwd = 2)
「ssm3.cpp」というファイルに以下のように実装します。
// ランダム効果付き、ポアソン分布のDGLM #includetemplate Type objective_function ::operator() () { // DATA // DATA_VECTOR(Y); // 観測値 // PARAMETER // PARAMETER_VECTOR(mu); // 状態 PARAMETER_VECTOR(r); // 観測誤差を表すランダム効果 PARAMETER(log_s_w); // 過程誤差の標準偏差の対数 PARAMETER(log_s_r); // ランダム効果の標準偏差の対数 PARAMETER(m0); // 状態の初期値 // PARAMETER TRANSFORMATION // Type s_w = exp(log_s_w); Type s_r = exp(log_s_r); vector lambda = exp(mu); // 平均個体数 vector lambda_noize = exp(mu + r); // 平均個体数(ノイズあり) // Main int T = Y.size(); // サンプルサイズ Type nll = 0.0; // 負の対数尤度 // ランダム効果 for (int t = 0; t < T; t++) { nll -= dnorm(r(t), Type(0.0), s_r, true); } // 状態の初期値から、1時点目の状態を得る nll -= dnorm(mu(0), m0, s_w, true); // 状態方程式に従い、状態が遷移 for (int t = 1; t < T; t++) { nll -= dnorm(mu(t), mu(t - 1), s_w, true); } // 観測方程式に従い、観測値が得られる for (int t = 0; t < T; t++) { nll -= dpois(Y(t), lambda_noize(t), true); } ADREPORT(lambda); return nll; }
推定します。random = c("mu", "r")とrについても設定するのを忘れないようにします。
# コンパイル
TMB::compile("ssm3.cpp")
# モデルのロード
dyn.load(dynlib("ssm3"))
# パラメータ推定の実施
dat <- list(Y = c(y))
pars <- list(
mu = rep(0, length(y)), m0 = 0,
r = rep(0, length(y)),
log_s_w = 0, log_s_r = 0)
obj <- MakeADFun(
dat, pars, random = c("mu", "r"),
DLL = "ssm3", silent = TRUE)
opt <- nlminb(obj$par, obj$fn, obj$gr)
推定結果です。正しくはs_wが0.4、s_rが0.5なので少しずれてしまいました。
> # 推定結果
> opt
$par
log_s_w log_s_r m0
-1.2297256 -0.3595145 -0.9732823
$objective
[1] 209.3599
$convergence
[1] 0
$iterations
[1] 11
$evaluations
function gradient
13 11
$message
[1] "both X-convergence and relative convergence (5)"
>
> # 推定された標準偏差
> opt$par[1:2] |> exp()
log_s_w log_s_r
0.2923728 0.6980151
結果は略しますが、推定結果の詳細は以下のように確認できます。
# 推定された状態 sdrep <- sdreport(obj) summary(sdrep) summary(sdrep, select = "random") summary(sdrep, select = "report")
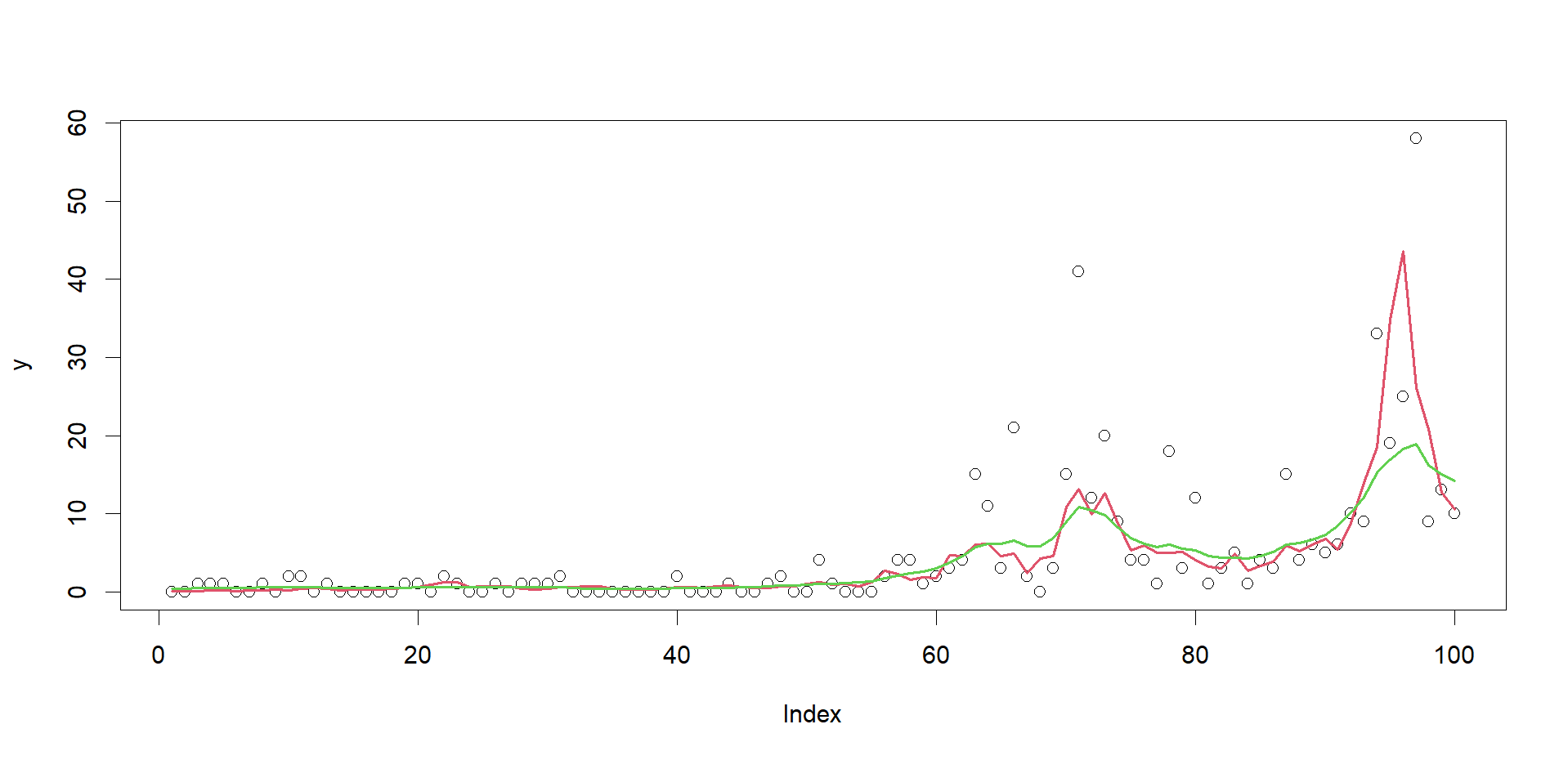
推定された「ノイズを排除した平均個体数lambda」の値を可視化します。シミュレーションの想定とある程度近い結果になっているようです。
# 可視化 plot(y) lines(exp(mu), col = 2, lwd = 2) summary(sdrep, select = "report")[, 1] |> ts() |> lines(col = 3, lwd = 2)
今まで当方は、このような複雑なモデルはベイズ推論を使って推定してきました。しかし、ラプラス近似を用いることで、非常に高速にモデルが推定できましたので、状況に応じて使い分けていきたいと思います。
万が一誤りなどあれば、ご指摘いただけますと幸いです。