1章 t検定(数式なし)
データの比較を客観的に行うために、t検定と呼ばれる手法を理解しましょう。
最初に、数式を使わない説明をします。そのあとで、もう一度同じ説明を数式を用いて行います。
1-1 期待値(平均値)
1-2 分散
1-3 有意差
1-4 サンプルサイズ
1-5 t値
1-6 t検定
1-7 p値
1-8 p値と検定
1-9 検定は偉いのか?
1-1 期待値(平均値)
最初に期待値について説明します。
期待値とは、比較する対象です。データを手に入れたとき、そこには数値がたくさんあると思います。その数値を全部そのまま扱おうとすると大変です。
例えば、以下の二つのデータを比較したいと思ったとしましょう。
データ①{1,3,5,10}
データ②{6,7,8,9 }
どちらの方が大きそうですか?
最小の値は1で、それはデータ①に含まれています。だから①の方が小さい?
最大の値は10で、それはデータ①に含まれています。だから①の方が大きい?
比較の仕方はたくさんあります。全部試すのは誠実なやり方かもしれませんが、面倒です。
たくさんのデータを要約した値を使ったほうが楽です。
その要約した値こそが期待値です。
期待値は平均値と大体同じです。第1章では議論の簡単のため同じものとして扱います。期待値と読めば、平均値と脳内変換してください。その違いは2章で説明します。
期待値の特徴を説明します。
- 期待値は、各々の値が大きければ大きいほど大きくなります。
- ただし、「大きな値」があっても、その「大きな値」が生じにくければ、期待値はあまり大きくなりません。
気温の例でいえば、(1)により、暑い日があれば気温の期待値も大きくなることがわかります。しかし、(2)により、100日中暑い日がたった1日しかないということであれば、気温の期待値はあまり高くなりません。
大阪の気温が10個、東京の気温が10個あったとき、どちらのほうが暑いか、ということを調べようと思ったら、各々の気温の期待値を取って比較すればいいわけです。例えば、大阪の気温の期待値が20度で、東京の気温の期待値が19度だったとします。そしたら「大阪の方が暑い」と一瞬でわかります。少なくとも20個のデータを全部見るよりかは楽です。
「データを比較する」という行為を、これからは「期待値(平均値)の大小を比較する」という言葉に置き換えることができます。
そうすれば比較がとても簡単になります。
期待値って便利ですね。
とはいえ、期待値(平均値)だけなら、本書を読む前に知っていた方も多いでしょう。
もうちょっと議論を進めていきます。
1-2 分散
分散は「データが期待値からどれほど離れているか」を表す指標です。
期待値は便利だと説明しました。比較が楽になるからです。
しかし、期待値を比較するだけではうまくいかない場合があります。
たとえば、電子顕微鏡を用い、0.001mm単位で大きさを測ったとします。リンゴAの大きさの期待値が10cmで、リンゴBの大きさの期待値が11cmでした。
一方、5年前に買った折れ曲がった定規で大きさを測りました。曲がっているので測るたびに値が変わるのですが、なんとなくリンゴAの大きさの期待値が10cmで、リンゴBの大きさの期待値が11cmになったような気がしました。
さて問題。リンゴの大きさの期待値の比較が「できる」のはどちらで「できない」のはどちらですか。
電子顕微鏡を使った結果を用いて比較するのはOKです。
でも、曲がった定規で測った結果で比較するのは普通ダメです。
この違いはどこにあるのでしょうか。
この違いを数値で表すことができるのが分散です。
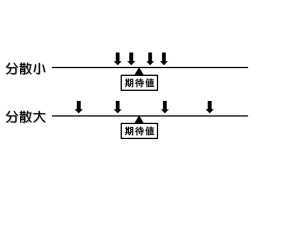
分散の大小を図で表しました。下向きの矢印がリンゴの大きさ(データ)を表しています。
分散は「データが期待値からどれほど離れているか」を表す指標です。
分散が小さければ、データは期待値の周りに集まっています。
分散が大きければ、データは期待値から遠く離れた場所に散らばっています。
データを代表する値として期待値を使おうとしていたはずです。なのに、期待値とデータが離れていたら、「データを代表する値」として期待値を使うことができなくなります。よって、分散が大きければ、期待値は比較の役に立ちません。
期待値を使うとデータの比較が圧倒的に楽になります。しかし、期待値だけしか見ないと、大きな過ちを犯すかもしれません。
1-3 有意差
「有意差」という言葉をご存知でしょうか。読んで字のごとく「意味の有る差」のことを指します。意味の有る差があれば、意味の無い(あるとは言えない)差もあります。この違いはなんでしょうか。そして、意味の有る差(有意差)は、どんなタイミングで出てくるのでしょうか。
リンゴの大きさの期待値に有意差があるかどうかは、
- リンゴの大きさの期待値の差が、リンゴの種間で大きい
- 例:リンゴAが1cm、リンゴBが100cm
- その期待値が信用できる→分散が小さい
- 例:両種のリンゴは電子顕微鏡で大きさを測定した
ということが大事そうです。
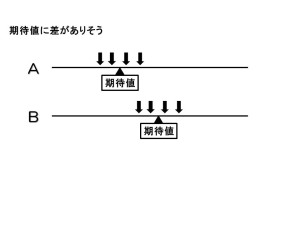
上の図が、期待値が比較に使える場合です。下向きの矢印がリンゴの大きさ(データ)を表しています。リンゴAとリンゴBではきっと大きさが異なるとみてよいでしょう。電子顕微鏡を使ったら、きっとこんな結果が出ます。
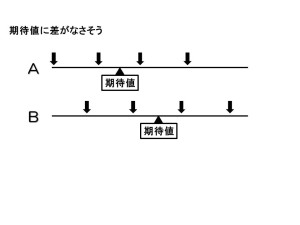
一方、2つ目の図は、期待値が比較に使えない場合です。リンゴAの大きさの期待値とリンゴBの大きさの期待値の値は先ほどと変わっていません。しかし、各データが期待値からかなり遠くに離れてしまっています。この図から期待値マークを取り外してみると、データに大小の差があるとは思えなくなるのではないでしょうか。この時はたとえ期待値に差があったとしてもその期待値の差は「意味の有る差とは言えない」ことになります。
期待値の差が大きくても、それが意味の有る差だとは限りません。
逆に、期待値の差が小さくても、電子顕微鏡を使って精密測定すれば、意味の有る差が出るかもしれません。
繰り返しになりますが、リンゴの大きさの期待値に有意差があるかどうかは、
- リンゴの大きさの期待値の差が、リンゴの種間で大きい
- その期待値が信用できる→分散が小さい
ということが大事です。
このこと、ぜひご銘記下さい。
1-4 サンプルサイズ
一回の調査(サンプリング)で得られたデータの個数を、サンプルサイズと言います。
電子顕微鏡でリンゴの大きさを10個測ればサンプルサイズ10です。
15人にアンケートを取れば、サンプルサイズ15です。
データを比較するときは、データの数も重要な要素となります。
サンプルサイズが小さい時のことを想像してみてください。
極端に、サンプルサイズが1だったとします。
広い農家の中で、「たまたま」日陰で、肥料もなく、支柱を指すのを忘れていたという恐ろしい環境下で育ったリンゴAと、「たまたま」ベストな環境で育ったリンゴBの大きさを比較するのはよくなさそうです。
たくさんたくさんのサンプルを集めて、極端な話、農家全部のリンゴAとリンゴBの大きさを測ったとします。農地の中でもいい場所悪い場所多々あるでしょう。しかし、いい場所で育ったリンゴA、悪い場所で育ったリンゴA、いい場所で育ったリンゴB、悪い場所で育ったリンゴB、全部そろっているならば、十分比較に耐えられます。
という訳で、データの比較にはデータのサンプルサイズが重要であり、サンプルサイズは大きいほうがよいという話でした。
1-5 t値
データを比較するというだけなのに、結構いろいろな指標が出てきました。
まとめてみます。
1.期待値
2.分散
3.サンプルサイズ
比較を簡単にするために期待値を使ったはずが、また指標が増えて比較が難しくなったとなれば本末転倒。
これらを一つの指標にまとめます。
さて、ここで意味の有る差「有意差」が出そうな条件を思い出してください。
リンゴの大きさの期待値に有意差がある場合は、以下の条件を満たすはずです。
- リンゴの大きさの期待値の差が、リンゴの種間で大きい
- その期待値が信用できる→分散が小さい
- サンプルサイズが大きい
・期待値の差は大きいほうがいい
・分散は小さいほうがいい
・サンプルサイズは大きいほうがいい
という訳で、上記3つをまとめるとこうなります。
$$t値=\frac{期待値の差}{分散的なもの\divサンプルサイズ的なもの}$$
まとめたものをt値と言います。
上記の式では「分散的なもの」などと歯切れの悪い書き方をしていますが、大体一緒です。どこが違うかは、次章、『t検定(数式あり)』をご参照ください。
※ Web版追記:次章はこちらから見ることができます。
t値が大きければ
- リンゴの大きさの期待値の差が、リンゴの種間で大きい
- その期待値が信用できる→分散が小さい
- サンプルサイズが大きい
上記の3要素を満たしたことになります。
という訳で、データを比較したければ、t値を計算して、その値が大きいか小さいかを調べればいいわけです。
大きければ有意差あり。リンゴAとリンゴBの大きさの期待値は有意に異なると言えます。
是非、大きいほうのリンゴを売り込みましょう。
1-6 t検定
さて、先ほど「t値が大きければ有意差ありなのだ」と適当なことを申し上げましたが、t値は、どれほどの値を取れば「大きい」とみなせるのでしょうか。
2を超えたら大きい? 3を超えたら大きい? 微妙です。
という訳で、t値が大きいか小さいかを判定しなければいけません。
そこで用いられるのが検定です。
以下、簡単な説明を試みます。正確なところは本書後半の「パラメトリックブートストラップ検定」の節をご参照ください。
t値と呼ばれる値を計算するとp値と呼ばれる値に変換できます。変換です。t値とサンプルサイズが与えられれば、p値は計算できます。
t値が大きければp値は小さくなります。
そして、p値は基準が定まっています。p値は0.05を下回れば小さいとみなす、と伝統的に決まっています。
という訳で、
1.t値をp値に変換する
2.t値が大きければp値は小さくなる
3.p値が0.05を下回るくらい小さければ、t値は十分大きいと言える。
上記の3ステップを踏むことで、t値の大小判定ができます。
t値を計算~その大小判定~有意差があるかどうかを決めるという一連の手続きのことをt検定と呼びます。
1-7 p値
p値について、何も説明をしていなかったので補足します。
サンプルサイズのところで少し説明しましたが、データを比較する際にとても怖いのが「たまたまそうなった」という「たまたま」「偶然」です。
広い農家の中で、「たまたま」日陰で、肥料もなく、支柱を指すのを忘れていたという恐ろしい環境下で育ったリンゴAと、「たまたま」ベストな環境で育ったリンゴBの大きさを比較するのはよくなさそうです。
t値も「たまたま」大きな値になることがあり得ます。
「偶然」環境最悪のところで育ったリンゴAが10個と、環境最高のところで育ったリンゴBを比較すると「たまたま」t値がとても大きな値になることがあります。
本来はリンゴAとリンゴBで大きさが変わるとは言えなかったとしても、です。
その「たまたまそうなる確率」のことがp値です。
例をあげましょう。
t値が1.9で、p値が0.1になったとします。このp値=0.1の意味を理解していただくのが今回の具体例の目的です。
農地にリンゴAとBが植わっていたとします。
リンゴAとリンゴBという品種を区別しないで、適当に10個ずつリンゴをサンプリングして、大きさを測りました。
そして、t値を計算してみました。
この作業を、100回繰り返したとします。
大概において、t値は小さい値をとるでしょう。品種を分けてないのですから、「リンゴA同士の比較」や「リンゴB同士の比較」をしている時だってあるはずです。なので差があるとは思えません。
しかし、生育場所の違いなどによって「たまたま」高いt値が出ることがあります。
調べてみると100回のうち、t値が1.9を超えた回数は10回でした。
ゆえに、t値=1.9の時、p値は10÷100=0.1となります。
まとめます。
t検定におけるp値とは、「本来差があるとは言えないデータ間で比較してt値を計算した時、今回与えられたt値よりも大きなt値が、『たまたま』でてくる確率のこと」です。
1-8 p値と検定
なお、もう少し正確に言うと、p値はt値だけでなくサンプルサイズもかかわってきます。サンプルサイズが大きいほうが「たまたま」差があるように見えてしまう危険性が小さくなります。なので、サンプルサイズが大きいほうがp値は小さくなりやすいということも覚えておくとよいでしょう。
t値は大きければ有意差ありでしたね。でも、t値が大きいとみなせるかどうかが不安であると。
そこで、「t値が、今回計算された値を『たまたま』超える確率」を求めます。この確率が小さければ、「たまたまそうなっただけ」という疑いを晴らすことができます。
t値が大きいと胸を張って言い張れます。
だから、t値が大きいかどうかを判定するのにp値を計算するのです。
1-9 検定は偉いのか?
「有意差」という言葉を覚えると(あるいは理解できると)とてもうれしくなってしまって、いろいろなことに有意差があるかどうか確認してみたくなります。
与えたえさの量によって養殖魚の体長が変わるか検定してみたい、や、雨の日と晴れの日で売り上げが変わるか検定してみたい、など。
大変結構なことだと思います。平均値を計算しておしまい、というよりかは、相当な進歩です。
また、あとで説明するように、検定はソフトを使えばとても簡単にできてしまいますから、実戦投入も容易です。
では、有意差が出れば万事解決なのでしょうか。
有意差がでれば、私たちは「データに基づく意思決定」が簡単にできるのでしょうか。
リンゴの大きさが品種で異なるか、という例を想像してください。
昔々に買った、折れ曲がった定規で大きさを測ると、有意差は出にくかったです。
一方、電子顕微鏡で正確に測ると、分散が小さくなるので、大きさに有意差あり、となりやすくなります。
あるいは、サンプルサイズを増やし、リンゴ1万個を使って検定すれば、もっともっと有意差は出やすくなります。
じゃあ、そうやって有意差が出て、リンゴAの方が大きくなったとしましょう。リンゴを買ってくれた消費者の方々は「リンゴAって大きくて素敵!」と思ってくれるでしょうか。
思わないでしょう。きっと。
電子顕微鏡を使って「リンゴAの大きさがリンゴBと比べて0.1cm大きい」ということがわかっても、それはきっと、商品の差別化要因にはなりません。
しかし、測定を精密にすれば、サンプルサイズを増やせば、有意差は出ます。
有意差は出せます。
有意差が出た時は、その「意味の有る」有意差に「価値が有る」のか、少し考えてみてください。
これは、「有意差」がどのようにして出されるのかを知っている人にしかできない特権です。
有意差の価値を理解するためにも、ぜひ「有意差」の意味を理解なさってください。
続きはこちらから読めます。
2章 t検定(数式あり)
3章 Rの簡単な使い方
書籍情報
|
平均・分散から始める一般化線形モデル入門 この記事の元となった書籍です。 書籍のサポートページはこちらです。 本文の第1部はこちらから読めます。 |
 |
注意
定価は2500円(消費税8%で2700円)ですが、Amazonさんなどでは在庫が不足しており、中古価格が高騰することがあります。
重版したので出版社には在庫が残っています。出版社のサイトからですと送料無料・書籍代は後払い・最短翌日出荷で、確実に定価で手に入ります。
以下のネット書店も併せてご利用ください。
|
|
|
|
|
新規作成:2015年7月12日
最終更新:2015年12月6日