単回帰

単回帰モデルを使った簡単な予測モデルのコードと説明です。

回帰 モデルの組み立て方から信頼区間や予測区間の求め方まで。
回帰分析って線を引っ張る以外のこともできるんですね。

目次

１．単回帰分析とは
２．サンプルデータ
３．回帰モデルを作る
４．予測区間の推定
５．理屈の話

１．単回帰分析とは

回帰分析とは、一言で言ってしまうとデータの散布図に線を引っ張るメソッドですね。Excelなどでもやったことのある方は多いはず。
しかし、信頼区間や予測区間を求めようと思ったら、Excelではとたんに面倒な計算をする羽目になってしまいます。Excelでは線を引っ張っておしまいなところを、Rをつかってもうちょっとマシな予測を出してみます。

２．サンプルデータ

下手に本物のデータを使うと著作権が怖いので自前で作りました

N<-100
b0<-5
b1<-3
x<-rnorm(N)
e<-rnorm(n=N,sd=2)
y<-b0+b1*x+e

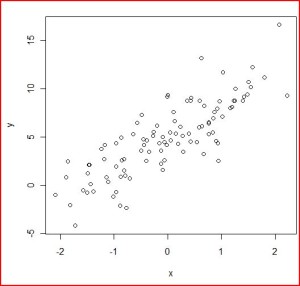
plot(x,y)

ようするに、正規分布の乱数（何も指定していないので平均＝0、分散＝1）で　x　を作って、切片5、傾き3になるように調整したんで すね。

３．回帰モデルを作る

細かい話は抜きにしますが、回帰モデルと言うものは「一般線形モデル」という枠組みに入っているモデルです。おなじみの分散分析等もまとめて「一般線形モデル」です。Rでも分散分析と回帰分析は同じ関数「lm」で計算できます（もちろん分散分析専用の関数もありますが）。
ここら辺の詳しい話は、ネット上にいくらでも落ちているので、ここでは割愛します。
このページで説明するのはあくまで「予測」だけということで。

モデルは以下の関数を実行すれば作れます

model<-lm(y~x)

1行で計算できるので楽ですね。結果は……

> model

Call:
lm(formula = y ~ x)

Coefficients:
(Intercept)            x
4.992        3.090

本来の切片は5、傾きは3だったのでまずまずの推定です（サンプルデータは乱数なので、計算するたびに値は変わります）。

４．予測区間の推定

predict関数を使うと一瞬

new<-data.frame(x=seq(min(x),max(x),0.1))

A<-predict(model,new,se.fit=T,interval=”confidence”)    #推定平均の95%推定区間付き
B<-predict(model,new,se.fit=T,interval=”prediction”)    #推定データの95%推定区間付き

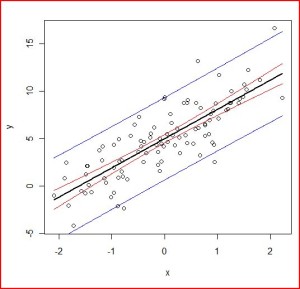
lines(as.matrix(new),A$fit[,1])
lines(as.matrix(new),A$fit[,2],col=”red”)
lines(as.matrix(new),A$fit[,3],col=”red”)

lines(as.matrix(new),B$fit[,2],col=”blue”)
lines(as.matrix(new),B$fit[,3],col=”blue”)

赤線が平均値の95%推定区間（信頼区間）青線がデータの95%推定区間（予測区間）です。

５．理屈の話

上記の内容は、ようするに「予測の話」にあったSEやSD（的なもの）を回帰分析においても計算してやって、信頼区間とか予測区間とかを出しているわけです。

SE、SDの使い分けは

A<-predict(model,new,se.fit=T,interval=”confidence”)    #推定平均の95%推定区間付き
B<-predict(model,new,se.fit=T,interval=”prediction”)    #推定データの95%推定区間付き

↑に注目

predict関数とはその名の通り予測値を返してくれる関数です。se.fit=Tにすると誤差の範囲も出してくれます。ここで、interval=”confidence”とinterval=”prediction”　とに分かれて いるのですが、これで「データの９５%誤差範囲」か「平均の９５%誤差範囲」を出してくれるわけです。confidenceのほうは平均の誤差（信頼区 間）で、 predictionの方はデータの範囲（予測区間）を表しています。　predict関数でlevelを指定してやると９５％以外の区間も計算ができるようです。level=0.90などと書けばOKです。

もっと詳しい説明です。

直接SEとかSD（的なもの）を計算してみます。
intervalを使わずに範囲を計算します。
まずはintervalなしの予測結果を作ってみます。

C<-predict(model,new,se.fit=T)

> C
$fit
1           2           3           4           5           6
-5.22512892 -4.91332049 -4.60151207 -4.28970364 -3.97789522 -3.66608679
・・・・・・・・・・・略

$se.fit
1         2         3         4         5         6         7
0.7073328 0.6869784 0.6666950 0.6464890 0.6263681 0.6063407 0.5864164
・・・・・・・・・・・・・略

$df
[1] 98

$residual.scale
[1] 2.23021

C $fitが回帰分析による予測値、C$se.fitが推定された回帰直線の精度を表しています。引っ張った回帰直線とは要するに予測された平均値なので、 これは平均値の幅を決めるのに用います（回帰直線が相手なので単純なSEの計算式とはやや異なりますが、だいたいそれと同じイメージで大丈夫です）。これ を用いると、平均値の９５%推定区間は

C$fit-C$se.fit*qt(0.975,C$df)　 　　　から

C$fit+C$se.fit*qt(0.975,C$df)　 　　　のあいだとなります。

こ こで　qt(0.975,C$df)　という変なものが登場しましたが、ここの確率を指定（この場合は９５%区間を求めているので、上側に残 り２．５％、下側に残り２．５％を残すため０．９７５をしていしてある）することによりいろいろな区間推定を行うことができます。２SEルールの「２」を いろいろ変えてやるわけですね。（前のページにも書きましたが、２SEルールの「２」は正確な値ではなくって大体の値です。実際には今回の場合は 1.984467となっています。この正確な値がqt(0.975,C$dfから計算されるのですね。この値はサンプル数によっても変わっ てきます）

ちなみに、A（平均値の９５%推定区間付き予測結果）という変数をみると

> A
$fit
fit         lwr          upr
1  -5.22512892 -6.62880785 -3.821449986
2  -4.91332049 -6.27660686 -3.550034119
3  -4.60151207 -5.92454651 -3.278477620
4  -4.28970364 -5.57264003 -3.006767250
5  -3.97789522 -5.22090231 -2.734888118
・・・・・・・・・・・・・・・略

$se.fit
1         2         3         4         5         6         7
0.7073328 0.6869784 0.6666950 0.6464890 0.6263681 0.6063407 0.5864164
・・・・・・・・・・・・・略
$df
[1] 98

$residual.scale
[1] 2.23021

というのが出てきますが、これのA$fitの　lwrとupr　の列が９５%区間を表しています。さきほど計算された上側・下側 ９５%推定区間と見比べてみてください。あっているはずです。

で、つぎは本命のデータの９５%推定区間（予測区間）です。

こちらは、さきほどの「平均値のばらつき」に、「データのばらつき」を　加える　というイメージで考えると分かりやすいです。平均値も実測値も完璧に正確 と言う訳ではないから、両方の誤差範囲を加えてやって、ようやく本当の誤差範囲が求まるんですね（実際にはもっとたくさんの推定誤差があるので、もっと計算はややこしくなるんですが、割愛します）。

よって予測データの９５%推定区間は・・・・・・

C$fit-sqrt(C$se.fit^2+C$residual.scale^2)*qt(0.975,C$df)　 　　から

C$fit+sqrt(C$se.fit^2+C$residual.scale^2)*qt(0.975,C$df)      の範囲内となります。

C$residual.scaleとかいうのが追加されました。こちらも　B　（推定データの95%推定区間付き推定結果）と見比べてみ てください。あってるはずです。

参考文献
山田作太郎・北田修一：生物統計学入門、第７章　回帰分析

※ 　SDやSEということばを（便利なので）使ってますが、回帰分析が相手なので、前ページの「予測の話」　に載せた内容とはやや異なります。でも、考え方 はよく似ているのでそのまま使いました。正確なSD、SEの話ではなく、造語としての２SDルールや２SEルールとして扱っているんだなと思って読んでく ださい。正確には、SDルールを「予測区間」、SEルールを「信頼区間」と呼ぶそうですが、ややこしい名称ですね。

前のページへ　⇒　予測の話
次のページへ　⇒　モデル選択_理論編