2章 t検定(数式あり)
第1章では、数式を使わないで、検定の仕組みを理解する、ということを目標にしてきました。
第2章では、数式を含めた説明をいたします。
数式は苦手という方もいるかもしれません。でも、逃げないでいただきたいです。数式はほとんどの人が読めません。だから、もし数式がほんの少しでも読めれば、とても大きな差別要因となります。英語よりも読める人は少ないはずです。
数式を使った統計学の世界を眺めてみてください。
そして、数式の読み方を学んでください。
書けなくてもいいです。読めれば大丈夫です。少しずつ、慣れてください。
2-1 期待値と平均値
最初に期待値について説明します。期待値とは、比較する対象です。
期待値は平均値と大体一緒ですが、意味合いが少し違います。期待値と平均値の使い方の違いについても理解してください。
期待値は以下の式で計算されます。piはあるデータが生じる確率、xiがそのデータの値、nがサンプルサイズです。
$$\sum_{i=1}^{n} p_ix_i$$
↑の式は言い換えるとこうなります。
期待値=『確率×その時の値』の合計
例を挙げます。
データが、{19が二つ、20が五つ、21が三つ}だとしたら、データの個数は合計10個より、
19になる確率 = 2÷10
20になる確率 = 5÷10
21になる確率 = 3÷10
よって期待値は以下のように計算されます。
$$19\times{\frac{2}{10}}+20\times{\frac{5}{10}}+21\times{\frac{3}{10}}=20.1$$
記号の読み方を説明します。
pが確率で、piと添え字「i」がついたものは、先ほどの例でいうと
p1 = 「19になる確率」 ( = 2÷10)
p2 = 「20になる確率」 ( = 5÷10)
p3 = 「21になる確率」 ( = 3÷10)
です。
xiは先ほどの例において、以下のようになります。
x1 = 19
x2 = 20
x3 = 21
期待値の特徴を復習します。
- 期待値は、各々の値(例においては19とか21とかいう数値)が大きければ大きいほど大きくなります。
- ただし、「大きな値」があっても、その「大きな値」が生じにくければ(確率piが小さければ)、期待値はあまり大きくなりません。
続いて平均値の定義を式で書きます。xがデータの値、nがサンプルサイズです。
$$\frac{1}{n}\sum_{i=1}^{n}x_i$$
データが、{19が二つ、20が五つ、21が三つ}だとしたら、平均値は以下のように計算されます。
$$\frac{19+19+20+20+20+20+20+21+21+21}{10}=20.1$$
期待値との違いを理解してください。
端的に言うと
・1/n
・pi
どちらを使うかというだけの話です。
{19が二つ、20が五つ、21が三つ}という例では、期待値も平均値も両方とも同じ値になります。
期待値と平均値は大体一緒です。
しかし、期待値の方が平均値よりも応用範囲が広いです。
例を挙げます。
あなたが株をやっていて、2020年5月1日に儲けることのできる金額を予想したいと思ったとしましょう。
株価が暴落すれば100万円損します。
暴落しなければ5万円儲かります。
さて、この時、期待値を「想像すること」は簡単です。
・株価が暴落する確率を5% (5/100)
・暴落しない確率を95% (95/100)
と仮に予想できれば、期待値は
$$-100\times\frac{5}{100}+5\times\frac{95}{100}$$
で計算できそうです。
では、2020年5月1日にあなたが儲けることのできる平均値はいくらになるでしょうか。
平均値を計算するためには一つ一つのデータが必要です。
2020年5月1日という日がたくさん必要になるのです。
2020年5月1日に儲ける金額の平均値は以下のようにして求められます。
・2020年5月1日という日が100日存在する
・100日ある2020年5月1日という日において、5日だけ暴落する。
・100日ある2020年5月1日という日において、95日は暴落しない。
ゆえに平均値は、以下で求まります。
$$\frac{-100-100-100-100-100+5+5+…+5}{100}$$
…のところは5が95個入ると思ってください。
これで期待値と同じ結果が導けます。
さて、期待値と平均値、使いやすいのはどちらですか?
きっと、期待値の方が状況を理解しやすいことと思います。
期待値は、「平均値をいろいろな状況で想像することができるように拡張したもの」だと思えばわかりよいでしょう。
これから先、個数を想像できない場面に出くわすことは多々あります。2020年5月1日という日が100日あることが想像できないのと同様に。
そんな時、平均値が計算できなくておしまい、では困ります。でも、期待値ならば、計算できます。想像できます。期待値ってすごいんです。
データの代表値としては、ぜひ期待値を使ってください。平均値との違いについて、ご納得いただければ幸いです。
2-2 分散の数式
期待値が終わったので、次は分散です。分散は以下の式で計算されます。
$$\frac{1}{n}\sum_{i=1}^{n}(x_i-μ)^2$$
nがサンプルサイズ、xiはそのデータの値、µはデータの期待値です。
nで割っていることに注目してください。分散は(xi-μ)2で計算されるものの平均値なのです。
平均値だということは、少し考え方を拡張すれば、期待値にもできます。
分散の期待値バージョンはこちら。
$$\sum_{i=1}^{n}p_i(x_i-μ)^2$$
1/nがpiに変わりました。
この式は言い換えるとこうなります。
分散=(1つ1つのデータ-期待値)2 の期待値
あるいは
分散=『データと期待値との距離』 の期待値
この式を理解するためには、まず(1つ1つのデータ-期待値)2という部分を理解しなければいけません。なお、(データ-期待値)のことを偏差と呼び、偏差を2乗したものの合計値を偏差平方和と呼びます。
この偏差平方和が大きければ、1つ1つのデータは、期待値から遠く離れています。
例を挙げます。
期待値:0
データその① : -0.1
データその② : +0.1
この時の(1つ1つのデータ-期待値)2の合計値は以下の通りです。
$$(-0.1-0)^2+(0.1-0)^2=0.02$$
小さいです。1つ1つのデータが期待値であるところの0からあまり離れていないからです。
一方、以下のようなデータならどうでしょうか。
期待値:0
データその① : -100
データその② : +100
$$(-100-0)^2+(100-0)^2=20000$$
大きいです。
期待値からデータが離れていれば、偏差平方和が大きくなることを確認してください。
ゆえに、分散は
分散=『データと期待値との距離』 の期待値
と解釈されます。
データを代表する値として期待値を使おうとしていたはずです。なのに、期待値とデータが離れていたら、「データを代表する値」として期待値を使うことができなくなります。よって、分散が大きければ、期待値は比較の役に立ちません。
よって、分散が大きければ、期待値を用いた比較を行っても、意味の有る差「有意差」は出にくくなります。
2-3 不偏分散
続いて不偏分散の説明に移ります。
まずは、「不偏」という言葉から説明します。
不偏とは、読んで字のごとく「偏りがない事」を意味します。
偏りのない分散のことが不偏分散です。
それでは、偏りのある分散とは何でしょうか。
それは、普通の分散のことです。前の節の計算式で求めた分散は、偏りのある分散だったのです。
なぜ偏りが生まれてしまうのか、説明します。
ここで気を付けるべきは、サンプリングはあくまでも「一部だけ抽出した結果でしかない」という事実です。
極端な例で説明します。
この世界にたった一軒しかない貴重な農家があります。この農家にリンゴが100個なっていたとしましょう。
覚えておいてくださいね、100個です。101個目のリンゴなど、この世界に存在しません。この世界に存在するすべてのリンゴの個数は100個です。
そして(少し極端ですが)、リンゴの大きさは1cm、2cmからはじまり、100cmまで、1cm刻みで100種類あったとします。
この時の、リンゴの「本当の」期待値は以下のようになります。
$$\sum_{i=1}^{100}0.01\times{x_i}=50.5$$
ただし
$$x_i={1,2,3,…,99,100}$$
です。
ここで、サンプリングをしました。リンゴは10個しかとりませんでした。無作為に抽出したつもりだったのですが、たまたま小さなリンゴが選ばれてしまったようです。サンプリングの結果は以下のようになりました。
$$x_i={1,2,3,4,5,6,7,8,9,10}$$
偶然、最も小さい1~10cmのリンゴが選ばれたとします。期待値は5.5です。
この時の分散はどうやって計算しますか。
分散の定義を思い出してください。
分散とは「データが期待値からどれだけ離れていると期待できるか」を表した数値でした。
ここで、とても重大な問題が発生します。
期待値は、「この世界に存在するすべてのリンゴをまとめた時の期待値」をつかうのが正確です。
でも、普通そんな期待値を計算することはできません。今回の例のように、農家の中のリンゴ全て、ならいざ知らず、世界中のリンゴの大きさを全て測って期待値を計算するなんて、不可能です。
よって、「サンプリングした結果計算された期待値」を用いて分散を計算するしかありません。
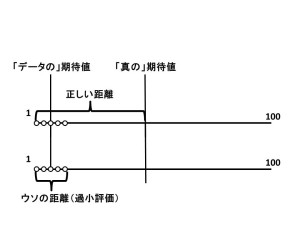
本当は「50.5から、データ(1~10)がどれだけ離れているか」を計算しなければいけないのに、「5.5から、データ(1~10)がどれだけ離れているか」を計算しているわけです。
当然、データと期待値の距離は小さくなります。分散は過小評価されます。
今回の例では、小さすぎるリンゴを偶然とってきましたが、逆に、91~100cmの大きいリンゴを10個取ってきても、同様に分散は過小評価されます。
ふつうにサンプリングして計算された分散は「小さく偏っている」のです。
なので、その偏りをなくすためには、分散を大きくしなければなりません。
よって、不偏分散は以下のようになります。
$$\frac{1}{n-1}\sum_{i=1}^{n}(x_i-μ)^2$$
ふつうの分散と違って、(n-1)で割っているところに注目してください。分母が小さくなったので、全体の値は大きくなります。「分散」というと、普通はこの不偏分散のことを指します。不偏でない過小評価された分散のことは「標本分散」などと区別して呼ばれます。
偏りをなくすために分散を大きくしているのだということ、ぜひご理解ください。
2-4 標準偏差
標準偏差は不偏分散の平方根(ルート)を取ったものです。
$$\sqrt[]{
\frac{1}{n-1}\sum_{i=1}^{n}(x_i-μ)^2
}$$
なぜ平方根を取るのかというと、そのほうが理解しやすいからです。式を見ればわかるように、分散はデータを2乗しています。ゆえに、単位も2乗されています。
単位が温度の2乗、「℃2」のままでは大変扱いにくいです。
理解を容易にするためにも、ぜひ平方根を取って、標準偏差を使いましょう。
2-5 標準誤差
次は標準誤差です。
標準誤差とは、端的に言うと、サンプルサイズを加味した標準偏差のことです。
思い出してください。期待値に有意な差を見出すためには、期待値の差が大きいということ以外に
・標準偏差(分散)が小さい
・サンプルサイズが大きい
の二つが必要になってくるのでした。
この両者をまとめてしまった指標が標準誤差です。
式はこちら。なお、σとは標準偏差のことです。よく出てくるので覚えておくと便利です。
$$\sqrt[]{
\frac{\frac{1}{n-1}\sum_{i=1}^{n}(x_i-μ)^2}{n}
}=\frac{σ}{\sqrt[]{n}}$$
標準偏差をサンプルサイズ(の平方根)で割っています。
ということは、標準誤差が小さければ
・標準偏差(分散)が小さい
・サンプルサイズが大きい
の両方が満たされていることになります。
標準誤差にはほかにもいろいろの意味が有るのですが、当面はこの程度の理解で問題ないと思います。
2-6 t値の計算例
t検定を、数式を使って確認してみましょう。
今回は、下記のようなデータセットを使用します。
$$x_i={-1,-1,0,0,1,3,5,6,7,7}$$
このデータの期待値は2.7なのですが、0以下の値も混じっています。
そこで、「このデータの期待値が0と有意に異なっているか」をt検定してみます。
この時のt値は以下で計算されます。
$$t値=\frac{期待値-0}{標準誤差}$$
分子が大きければ
・期待値と0との差が大きい
分母が小さければ
・標準偏差(分散)が小さい
・サンプルサイズが大きい
の両方が満たされていることになります。
t値が大きければ、有意になる3条件がそろいます。
t検定の完成まであと一歩です。
これをぜひ実データを使って計算したいのですが、計算が少々大変そうです。
という訳で、次章からRと呼ばれる統計ソフトの説明に移ります。
最小限のソフトの使い方をおさえたうえで、t検定を実行してみましょう。
続きや前の章はこちらから読めます。
1章 t検定(数式なし)
2章 t検定(数式あり)
3章 Rの簡単な使い方
書籍情報
|
平均・分散から始める一般化線形モデル入門 この記事の元となった書籍です。 書籍のサポートページはこちらです。 本文の第1部はこちらから読めます。 |
 |
注意
定価は2500円(消費税8%で2700円)ですが、Amazonさんなどでは在庫が不足しており、中古価格が高騰することがあります。
重版したので出版社には在庫が残っています。出版社のサイトからですと送料無料・書籍代は後払い・最短翌日出荷で、確実に定価で手に入ります。
以下のネット書店も併せてご利用ください。
|
|
|
|
|
新規作成:2015年7月13日
最終更新:2015年12月6日