Pythonの簡単な使い方：環境構築～データ読み込み～図示・モデル化

最終更新：2017年07月31日

この記事では、タイトルの通り、環境構築から簡単な文法の説明、numpy・pandasの機能を用いたデータの取り扱い、seabornを使った図示、最後はstatsmodelsを用いた一般化線形モデルの推定までを一気に流します。
Pythonを高機能電卓として使うために「Jupyter Notebook」というデータ解析環境を構築して、そこでコードを実行するようにします。
多少複雑な計算でもPythonで簡単に扱うことができることを確認してください。
インストールも、2017年現在、大して難しくありません。

※この記事は、OSとしてWindowsを使っていることを前提としています。
※numpyやseabornという横文字が意味不明だ、という方でも特に問題ありません。ただのライブラリの名前ですので気になさらないでください。

Jupyter Notebookでの計算結果については、こちらからhtml形式で閲覧することができます。

スポンサードリンク

スポンサードリンク

目次

1. Pythonとは
2. PythonのインストールとJupyter Notebookの起動方法
3. 計算の実行方法とShift ＋ Enter
4. Pythonによる簡単な計算
5. 「変数に格納する」という言葉の意味と使い時
6. コメントの使い方
7. 様々なデータの型
8. データの読み込み
9. グラフ描画
10. 一般化線形モデル(GLM)の推定

 

1．Pythonとは

Pythonには2つの顔があります。
一つはWebアプリなどを作ることができる、使いやすい汎用プログラミング言語という顔。
もう一つは、データ分析、機械学習を数行のコードで書くことができる「高機能電卓」という顔です。

Pythonを使うと、ネットショッピングなどができるWebサービスを作ることができます。
もちろんデスクトップ上で動くアプリを作ることもできるし、ゲームだって作れます。
これはPythonが汎用的なプログラミング言語だからです。

ここでは、まずはPythonを「高機能電卓」として扱う方法を説明します。
ここでPythonの基礎を学んでおけば、アプリ開発にも応用できるでしょう。

 

2．PythonのインストールとJupyter Notebookの起動方法

Pythonを直接インストールするのではなく「Anaconda」をインストールします。
Anacondaをインストールすると、Pythonだけでなく、統計解析などを行うためのツールをまとめてインストールすることができます。大変に簡単なので、ぜひAnacondaをインストールするようにしてください。

Anacondaは以下のURLからダウンロードができます。
https://www.continuum.io/downloads

基本的には「次へ」を押し続けていればインストールが可能です。
全角の文字が使われているフォルダにはインストールできないので、インストール中に怒られた場合は、適宜インストール先を変えてください。

Anacondaをインストールすると、Jupyter Notebookというのが勝手にインストールされています。
こいつが強力な電卓でして、複雑な計算でも、結果をすぐに表示してくれます。もちろんグラフ描画もできます。

インストールされた後、デスクトップに「Python」というフォルダを作ってみてください（フォルダの名前はなんでもOKです）。
そして、スタートボタンから「すべてのプログラム」→「Anaconda3」→「Jupyter Notebook」と選択します。
このJupyter Notebookを起動すると、黒い画面（コマンドプロンプト）が立ち上がった後、Google Chromeなどのブラウザが立ち上がり、以下のような画面が出てきます。

下の表にはフォルダの名称が出ています。
「Desktop」をクリックして移動し、さらに、先ほど作った「Python」フォルダへ移動します。

下の図のように「New」→Python3」を選択します。

すると、以下の図のような画面が出てきます。

これで準備完了です。
「In」と書かれているセルにコードを書いていけば、計算結果を出力してくれます。

 

3．計算の実行方法とShift ＋ Enter

例えば以下のようなコードを書いてみます。

1 + 1

これを実行すれば、きっと2になるのでしょう。
しかし、普通に「Enter」を押しても、改行されるだけで実行されません。
実行する場合は、「Ctrl + Enter」を押します。同時押ししてください。
すると2が出てきます。

次は、同じセルを選択して「Shift + Enter」を同時に押してみます。
すると、計算結果が出たうえで、さらにセルが追加されました。

コードを書いて「Shift + Enter」を押していくと、どんどん計算結果が出てきます。
この使い方だけ覚えておいてください。

 

4．Pythonによる簡単な計算

まず、四則計算は簡単にできます。

1 + 1
3 – 4
5 * 2
6 / 3

2乗する場合は「**」という記号を使います。

4 ** 2

平方根を計算する場合は、以下のようにします。

import numpy as np
np.sqrt(16)

これは少々複雑なので、解説します。
Pythonは、何でもできる汎用的なプログラミング言語だと説明しました。しかし、初期状態ではできることがあまり多くありません。特に数値計算をする場合は、機能が相当に不足していると思ってもらって間違いないです。

そこで追加機能をインポートします。
それが「import numpy」です。
numpyというのが有名な数値計算ライブラリ（追加機能）なので、それをインポートしているわけです。

で、このnumpyの中に入っている機能を使おうと思った場合は以下のように記述するのが普通です。

import numpy
numpy.sqrt(16)

numpyの中に入っている機能を使ってください、と指定するために「numpy.」と記述していることに注目してください。
これでも正しい値（４）が計算できます。
が、毎回毎回numpyと書くのは面倒くさいです。
そこで「import numpy as np」と「as np」というオプションを追加します。
すると、次回以降は「numpy」と書くべきところを省略して「np」とだけ書けばよくなります。楽ですね。

というわけで、以下のようにして、平方根を求めるということでした。

import numpy as np
np.sqrt(16)

 

5．「変数に格納する」という言葉の意味と使い時

Pythonにかぎらずプログラミングにおいてとても重要な「変数」という考えを学んでいただきます。

変数とは、値を格納する入れ物です。
例えば、

x = 1

とエディタに入力したとしましょう。
すると、1という数値がxと呼ばれる入れ物に格納されます。「=」という記号が「格納する」という動作を表します。
なお、xという名前はなんでもよくて、Dataとかsuutiとか、なんでも好きな名前を付けてください。
そして、いったん値を格納してしまえば、自由にそれを使うことができます。

x + 1
と入力してShift + Enterすると、２が答えとして出てきます。

なお、中に入っている値を見たい場合は、変数の名前だけを打ち込んで実行します。

地味ですが重要なテクニックなので覚えてください。

なお、変数に値を格納することを「定義する」と呼ぶこともあります。先ほどの例では「xに1を定義した」ことになります。

定義されていない変数を使うとエラーが出ます。

—————————————————————————
NameError Traceback (most recent call last)
in ()
—-> 1 a

NameError: name ‘a’ is not defined

 

6．コメントの使い方

コメントにはいくつかの入力方法があります。
まずはセルに「#」を入れてから実行すると、その行がコメントとなります。

以下のコードを記述して、実行しても、計算結果は出てきません。
# コメントです
# 1 + 1

また、下の図のように、Markdownを選択すると、見出しを付けることができます（デフォルトはCodeです）。
後で見直す時に便利ですね。

以下の内容は、こちらのPythonでの実行結果のデモを参照しながらご覧いただければと思います。
このデモも、マークダウンを使って見やすくなるように整形してあります。レポートを作る際にも便利ですね。
なお、リンク先のHTMLファイルは、JupyterNotebook左上の「File」～「Download as」～「HTML(.html）」を選ぶことによって作りました。

 

7．様々なデータの型

1+1くらいなら簡単に計算ができるのですが、統計処理を実装するためには多くのデータを保存してそれを取り扱う必要が出てきます。
そんな時に「いろんなデータを保存しておくデータの型」を覚えておくと便利です。

Pythonにはリストだのタプルだの山ほどのデータの型があるのですが、とりあえずarray（配列）とデータフレーム（DataFrame）の2つを覚えておけば不便しません。
順に解説します。

まず、前提として、arrayもDataFrameもPythonの標準機能には入っていません。
arrayはnumpyを、DataFrameはpandasというライブラリを読み込む必要があることに注意してください。
なので、以下の3行は、JupyterNotebookを立ち上げたときに、常におまじないとして唱えておくのが良いかと思います。

import numpy as np
from pandas import Series,DataFrame
import pandas as pd

まずはarrayを作ってみます。
以下のコードで、１，２，３，４，５という数値の入ったarrayを作ることができます。
sample_arrayという名称で作ってみましょう。

sample_array = np.array([1,2,3,4,5])

こんな結果が出てきます。

array([1, 2, 3, 4, 5])

そのまんまですね。

あまり面白くないのですが、次のDataFrameに格納するために、いったんarrayを介することが多いですので、とりあえず覚えておいてください。

データフレームですが、以下のようにarrayを使って作ることができます。

pd.DataFrame({‘col1’:sample_array})

なお中カッコでくくった部分が、データの中身となります。
col1という列名で、先ほど作ったsample_arrayを格納しました。

結果についてはこちらのPythonでの実行結果のデモを見てください。
表形式で結果が表示されます。
これはなかなか見やすくていい感じです。

複数列を持たせることもできます。

pd.DataFrame({‘col1’:sample_array, ‘col2’:np.array([6,7,8,9,0])})

col2に関しては、新しくnp.arrayでarrayを作ったものを格納しました。

 

8．データの読み込み

自分でデータをセコセコ打ち込むのは大変ですので、普通はCSVやExcelのファイルを読み込みます。
ここでは、「近所の草むらにおける、えさの量と猫の数の関係」というデータを読み込んで解析することにします（架空のデータです）。

もしあなたがDeskTop上の「Python」というフォルダで作業をしているならば、そこに以下のファイルを配置してください。

poissonData

あとは、この一行で、データの読み込みが完了します。
dataという変数に格納しておきました。

data = pd.read_csv(“poissonData.csv”)

クリップボードからも読み込むことができます。
これだと、ExcelでもCSVファイルでも、ファイルの形式を考えずにデータを読み込むことができるので便利です。
データを選択して、コピーをしてから、以下のコマンドを実行すればデータが読み込まれます。

data2 = pd.read_clipboard()

 

9．グラフ描画

次はグラフの描画です。
こちらも多くのライブラリを追加で読み込む必要があります。
後にGLMを推定するので、そのためのライブラリも併せて一括で読み込んでおきます。

# 統計モデルを推定するライブラリ
import statsmodels.api as sm
import statsmodels.formula.api as smf

# グラフを描画するライブラリ
from matplotlib import pyplot as plt
import seaborn as sns
# グラフをjupyter Notebook内に表示させるための指定
%matplotlib inline

最後の『%matplotlib inline』が忘れやすいですが重要です。
これがないと、グラフが表示されません。忘れずにつけるようにしてください。

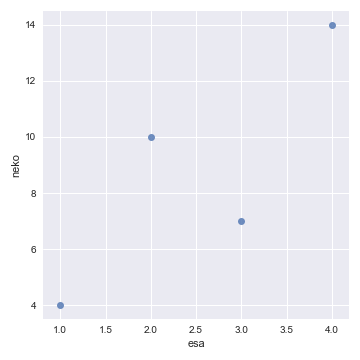
散布図を描くには、以下のコード一発で済みます。

sns.lmplot(x=”esa”, y=”neko”, data=data,fit_reg=False)

なかなかきれいなグラフです。
横軸のesa（えさの量）が増えると、縦軸のneko（猫の個体数）が増えていくように見えます。

最後に少し補足をしておきます。
グラフを描画するライブラリとしてもっとも有名なものは「matplotlib」と呼ばれるライブラリです。
しかし、このライブラリは設定が難しい上にグラフがややダサいという欠点があります。
そこでmatplotlibのラッパー（matplotlibのカスタマイズだと思ってもらえればOKです）である「seaborn」をここでは使っています。
seabornをインポートするだけで、グラフの見栄えが飛躍的に良くなりますので、是非こちらを使うようにしてください。

 

10．一般化線形モデル(GLM)の推定

では、GLMします。
設定で1行、モデルの推定で1行、結果の表示で1行の3行で計算ができます。

# ポアソン回帰のモデルの設定
glm_pois = smf.glm(formula=”neko ~ esa”, data=data, family=sm.families.Poisson())

# fitという関数を実行すると、モデルが推定される
result_pois = glm_pois.fit()

# 結果の表示
result_pois.summary()

順番に解説します。
まずは、GLMの設定です。
今回は猫の個体数を応答変数としています。猫の数はマイナスになることはあり得ませんし、小数点以下の値をとることもあり得ません。そんなときにはポアソン分布を使ってモデル化をするのがセオリーです。
『formula=”neko ~ esa”』で、「猫の数の多少を、えさの量で説明するモデルを作ります」と設定します。
『data=data』でデータの指定をします。先ほどCSVファイルから読み込んだデータの名称を「data」としていたことを思い出して下しさい。
『family=sm.families.Poisson()』でポアソン分布の指定をします。

2行目のモデルの推定に関してはいいでしょう。1行目で設定された結果に対して「fit()」という関数を適用します。
推定された結果を基に3行目で結果の表示を行います。「summary()」という関数を適用します。

計算された結果を使って関数を適用するときに「結果が格納された変数.関数」というように「ドット」を使って連結していることに注意してください。ここはR言語と大きく異なります。
「結果が格納された変数」には、計算結果だけではなく実行することのできる関数も格納されています。なので、それを呼び出したのだとご理解ください。

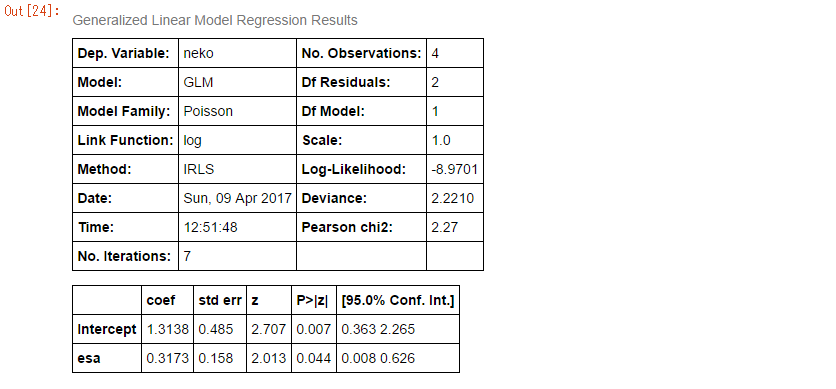
計算結果はこちら。

表形式で結果が出力されるので、とても見やすいですね。

一番興味のあるのは、下の表でしょうか。
esaと書かれた行を見てください。
coef列が0.3173とあります。プラスの値になっているので、やはり餌が増えると猫の数も増えそうだということがわかります。
右から2つ目の『P>|z|』はp値です。0.05を下回っているため、「えさの量は猫の数の多少に対して有意な影響を持っている」と主張することができます。
なお、このp値はWald検定の結果を使っているようです。

最後に、GLMで予測した結果を図示してみましょう。

まずは予測です。
予測をする前に、予測に使われる説明変数を用意しましょう。

esa_plot = np.arange(0, 5, 0.1)

『np.arange(0, 5, 0.1)』で、「０から５まで、0.1区切りのデータを作る」という指示を表します。
結果はこちら。

array([ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ,
1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2. , 2.1,
2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. , 3.1, 3.2,
3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. , 4.1, 4.2, 4.3,
4.4, 4.5, 4.6, 4.7, 4.8, 4.9])

array形式となっている点に注意してください。

次は、このesa_plotを使って、予測結果を出してみます。
以下の一行で計算ができます。
結果はarray形式で出力されます。

pred = result_pois.predict(exog = pd.DataFrame({‘esa’:esa_plot}))

『result_pois』とは、GLMした結果が格納された変数であることを思い出してください。
この変数に対してドット「.」を付けてからpredict関数を実行します。
引数には、説明変数を入れます。これはDataFrame型でなくてはならないことに注意してください。

後は図示です。

sns.lmplot(x=”esa”, y=”neko”, data=data,fit_reg=False)
plt.plot(esa_plot, pred)

難しい文法を覚えなくても、簡単なデータ分析であれば少しの知識と労力だけで実行可能です。
グラフも美しいし、なかなか良い言語だと思います。

今回の計算結果はすべてこちらから確認することができます。

 

WebでPythonを学ぶなら

実践 Python データサイエンス   動画でPythonやJupyter Notebookの使い方を学ぶことができる勉強サイトです。 Udemyを利用すると、Pythonやデータ分析を「基礎から順にステップアップする内容で、かつ動画で」学ぶことができます。 ネットで受ける通信教育、みたいな感じです。 管理人も受講してみました。体験記はこちらから読めます。

 

参考文献

Python入門[2&3対応]   Pythonの入門書は数多くあるのですが、管理人はこれを読みました。 そこそこ分厚いのですが、章ごとに独立しており、気が向いた時に気が向いた場所を読むことができます。 データ分析やJupyterNotebookについてはほぼ触れられていないですが、Pythonの基礎文法を学ぶにはいいと思います。 辞書のように使うのが良いでしょうか。

Think Stats 第2版 ―プログラマのための統計入門   Pythonでデータ分析をするための入門書です。統計学の理論に関する説明は少なめですが、とりあえずコードを書いて勉強したいという場合に良いかと思います。

平均・分散から始める一般化線形モデル入門   手前味噌ですが、管理人の書いた一般化線形モデルの入門書です。 最後に出てきたGLMの推定について、より詳しく知りたければこちらを参照いただければと思います。 なお、こちらではR言語を使っています。

書籍以外の参考文献

seabornのグラフの例がたくさん載っているサイトです。ソースも併記されているので、便利です。
http://seaborn.pydata.org/examples/index.html

スポンサードリンク

スポンサードリンク