非線形もOKな相関係数:MIC
予測をするための一つの方法として、データ同士の関連を調べる作業があります。
気温とビールの売り上げは関連があるということがわかれば、予測に役立つでしょう。
データがもっともっと多くなると、どのデータ同士が関連しているのかが判別しにくくなります。
そこで相関係数の出番ですね。
このページでは、データ同士に関連があるかどうかを簡単に判別できる指標、MICの解説をします。
目次
1.MICの概要(スライド)
2.RでMIC
1.MICの概要
すごくざっくりとMICの解説をしてみました。
そのココロはわかっていただけるのではないでしょうか。
細かい話は、ぜひ原著論文を参照してください。
2.RでMIC
MICは”minerva”と呼ばれるパッケージを使うことで簡単にRで計算できます。
install.packages(“minerva”)
としたあとで
library(minerva)
を実行したら準備完了です。
パッケージをインストールできない方は、Rのアイコンを右クリックして「管理者として実行」してRを起動させてからパッケージをインストールしてください。
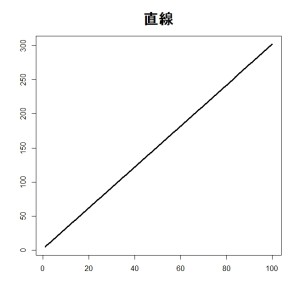
まずは、ふつうの直線の相関係数とMICを計算してみます。
# 直線
x <- 1:100
y <- 3*x + 2plot(y ~ x, xlab=””, ylab=””, type=”l”, lwd=3, main=”直線”, cex.main=2)
この時、MICはmineという関数で計算できます。比較用にcor関数で計算したピアソンの積率相関係数も入れておきます。
> mine(x,y)
$MIC
[1] 1$MAS
[1] 0$MEV
[1] 1$MCN
[1] 3.584963$`MIC-R2`
[1] -2.220446e-16
> cor(y,x)
[1] 1
MICもピアソンの積率相関係数も、共に1になりました。
mine関数にはMASとか変な値がたくさん出てきます。
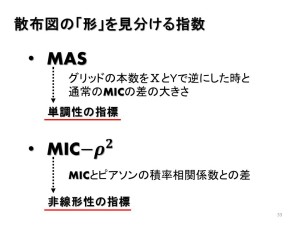
その中でも、先のスライドで解説していたMASとMIC-R2について軽く見ておきます。
先のスライドにも書いた通り、MASは単調性の指標(値が大きければ、単調でない)であり、MIC-R2は非線形性の指標(値が大きければ非線形である)です。
直線なので当然、単調(MAS=0)かつ線形(MIC-R2=0)です。
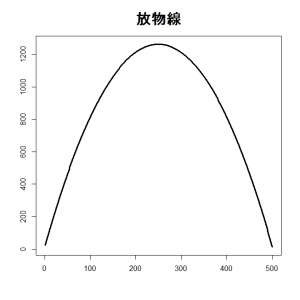
次は非線形なものを見てみましょう。手始めに放物線です。
# 放物線
x <- 1:500
y <- x*10 – 0.02*x^2 + 13plot( y ~ x, xlab=””, ylab=””, type=”l”, lwd=3, main=”放物線”, cex.main=2)
この時のMICとピアソンの相関係数は……。
> mine(x,y)
$MIC
[1] 0.9999964$MAS
[1] 0.6866988$MEV
[1] 0.9999885$MCN
[1] 3.906891$`MIC-R2`
[1] 0.9999364
> cor(y,x)
[1] -0.007745796
MICはほぼ1なのにかかわらず、corで計算されたピアソンの相関係数は全然だめですね。
また、MAS、MIC-R2ともに大きいため、単調でなく、かつ非線形であることがわかります。
グラフ見たほうが当然早いんですが、滅茶苦茶たくさんのデータを渡されたときに、瞬時に数値としてグラフの形状が推測できるというところにこの指標の価値があります。
たとえば、単調でない動きをしているデータを探したいのならば、手当たり次第にMASを計算したうえで、MASが0.5以上とか(0.5という数値は適当です)、何らかの基準を用いて抽出することによって、「グラフを描かなければならない回数」を大幅に減らすことができます。
ようするに、人間の労力を減らせるということです。
便利ですね。
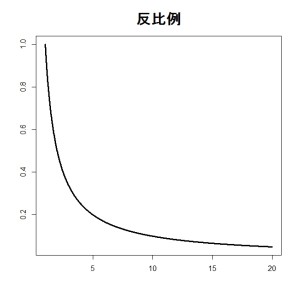
最後に反比例するデータでも計算してみます。
# 反比例
x <- seq(1,20,by=0.01)
y <- 1/xplot( y ~ x, xlab=””, ylab=””, type=”l”, lwd=3, main=”反比例”, cex.main=2)
計算結果はこちら
> mine(x,y)
$MIC
[1] 0.9999998$MAS
[1] 0$MEV
[1] 0.9999998$MCN
[1] 2$`MIC-R2`
[1] 0.4328682
> cor(y,x)
[1] -0.7530814
MASは0(すなわち単調)で、MIC-R2がやや大きいので、やや非線形であることがわかります。
次は、スライドにも載せていた、MICが1になってしまう状況を見てみます。
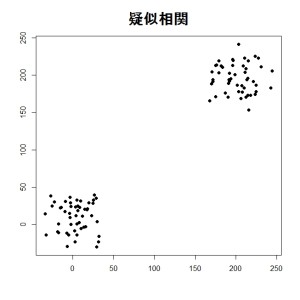
# 疑似相関
set.seed(10)
para <- 20
x2 <- c(rnorm(n=50, mean=10, sd=para), rnorm(n=50, mean=200, sd=para))
y2 <- c(rnorm(n=50, mean=10, sd=para), rnorm(n=50, mean=200, sd=para))plot(y2 ~ x2, xlab=””, ylab=””, pch=16, main=”疑似相関”, cex.main=2)
> mine(x2,y2)
$MIC
[1] 1$MAS
[1] 0.02663644$MEV
[1] 1$MCN
[1] 3.584963$`MIC-R2`
[1] 0.07479406
> cor(y2,x2)
[1] 0.9618763
MICは残念ながら1になってしまいますが、ふつうの相関係数もほぼ1なので、MICだけが悪いわけじゃありません。
でも、グラフの形状、データの関連性を相関係数だけで判別するのは難しいのかもしれませんね。
MICはあくまでも大きなデータを捌く際のとっかかりとして使われるべきで、最後には人間がグラフを描いてそれを眺めるという作業をしたほうが良いでしょう。
とはいえ、使いようによってはMICはとっても便利です。
参考文献
Detecting Novel Associations in Large Data Sets
→MICの原著論文です。リンクはこちら。(契約してないとPDFは見れない様子? 大学の中などなら読めるかもしれません)
Take a Risk:林岳彦の研究メモ(”相関”の話&そのついでに”21世紀の相関(MIC)”の話(ややマニア向け))
→MICという存在はこのブログで初めて知りました。興味深い内容なのでお勧め。
リンクはこちら。