時系列解析_ホワイトノイズとランダムウォーク

Rを用いた時系列解析 の実践例を載せます。

時系列解析ってなに？　という方は時系列解析_理論編を先に読まれるとよいと思います。
ここでは、本格的な時系列モデルを組む前に、予測がほぼ不可能であるホワイトノイズとランダムウォークの性質と和分過程の特徴を解説します。

モデルによる予測ができない時　１．ホワイトノイズ

これからARIMAモデルを推定していくわけですが、そもそも自己相関が全くない、すなわち過去から未来を予測できないデータをお目にかけます。

自己相関の無い完全な雑音のようなデータのことをホワイトノイズと言います。
このホワイトノイズをforecastパッケージのauto.arimaでモデリングしてみましょう。

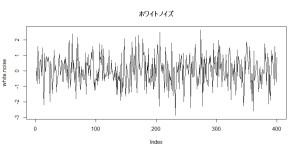
ホワイトノイズは下のコードで簡単に作れます。

set.seed(1)
white.noise <- rnorm(n=400)
plot(white.noise, type=”l”)

set.seedはおまけみたいなものなのであまり気にしないでください。シミュレーションデータは本来ならば毎回違う値が出されるんですが、set.seed()を使うことによってデータを固定することができます。本題とは離れるので、細かい解説は省略します。

rnormが重要なところですが、これは正規分布に従う乱数を発生させる関数です。meanやsdといったオプションを何も指定していないので、平均0で標準偏差1の標準正規分布に従う、何の自己相関もないノイズが生成されます。

さて、これで何の自己相関もない純然たるノイズを作ることができました。
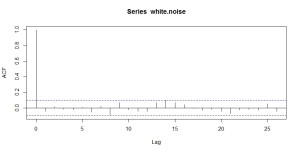
本当に自己相関がないのか確認してみましょう

acf(white.noise)

 

やっぱり自己相関はありませんでした。
すなわち、もし仮にこのホワイトノイズが2000年から2001年まで一日ごとにとられたデータであるならば、2000年5月5日のデータを手に入れたとしても2000年5月6日の予測はできないということです。

もしこんなホワイトノイズにARIMAモデルを適用するとしたらどんなモデルになるでしょうか。やってみます。

library(forecast)

model.noise <- auto.arima(
white.noise,
ic=”aic”,
trace=T,
stepwise=F,
approximation=F
)

前回紹介したforecastパッケージを使います。CRANからパッケージをインストールした後に上記のコードを実行してください。

auto.arimaの引数として、上から順に、
・データの指定
・情報量基準の指定
・計算の途中経過を表示させる
・計算をケチらない
・計算をケチらない
です。
計算をケチらない指定が二つもありますが、一つ目のstepwiseは、最適な次数を探す際に次数を総当たりで調べなさいという指定で、approximationは実際にモデルを計算するときに、近似法を使うなという指定です。
やや時間が余分にかかるものの、正確に計算しようと思った場合は両方Fにしておくとよいでしょう。

もしもマルチコアのPCを使っている場合は、stepwise=Fの場合に限り
parallel=T
と追加で指定することで、やや高速に計算をさせることが可能です。

結果はこちら

> model.noise
Series: white.noise
ARIMA(0,0,0) with zero mean

sigma^2 estimated as 0.9391: log likelihood=-555.01
AIC=1112.03 AICc=1112.04 BIC=1116.02

ARIMA(0,0,0)、すなわち、ARモデルの次数もMAモデルの次数もともに0、何にもパラメタを推定しないモデルが最も良いと判別されたわけです（データによってはたまに次数の選び間違いが生じることもあります。ホワイトノイズなのに自己回帰モデルが選ばれたり……）。

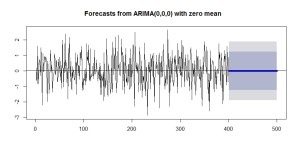
予測結果はこうなります。

plot(forecast(model.noise, h=100), flwd=5)
abline(h=mean(white.noise))

forecast関数を使うと一瞬ですね。
細かいですが、flwdは予測結果の線の太さの指定です。lwdだけだと、予測される前の線の太さの指定になってしまうので気を付けてください。

ablineを使って強調しておきましたが、予測値は単なる期待値と同じ値になります。
昨日の値を使って今日を予測することができない以上、こんな予測しか返せないんですね。

モデルによる予測ができない時　２．ランダムウォーク

次はランダムウォークを扱います。

ランダムウォークは、厳密に定義すると難しいのですが、ホワイトノイズのような乱数の累積和だと思ってください。

ですから、先ほど作ったホワイトノイズの累積和を取ると簡単にランダムウォークが作れます。
和を取っているので、これは和分過程ですね。
以前説明したように、差分をとったら元の系列に戻るものが和分過程でした。
今回の場合、差分をとったらもとのホワイトノイズに戻るということです。

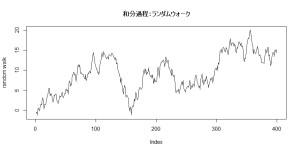
ランダムウォークデータを作ってみます。

random.walk <- cumsum(white.noise)
plot(random.walk, type=”l”, main=”和分過程：ランダムウォーク”)

cumsumは累積和を取る関数です。
データが１，２，３，４，５とあれば、cumsumすると１，３，６，１０，１５になるわけ。

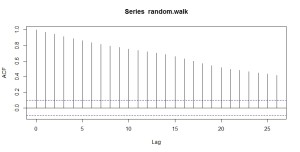
ランダムウォークの自己相関はこちら。

acf(random.walk)

ホワイトノイズと違って自己相関があります。
じゃあ予測が正確にできるのかというと、そうはいきません。

今回作ったランダムウォークはホワイトノイズの累積和でした。累積和はその定義上、「過去と同じ数字」を使っているわけです。
たとえばデータが１，２，３，４，５とあれば、cumsumすると１，３，６，１０，１５になりますが、

1つ目の累積和　１
2つ目の累積和　１＋２
3つ目の累積和　１＋２＋３
4つ目の累積和　１＋２＋３＋４
5つ目の累積和　１＋２＋３＋４＋５

と計算されますよね。これを見ればわかるように、5つ目の累積和は4つ目の累積和と4つも同じ数値が使われています。
同じ数値が使われる＝似てる＝自己相関がある、です。

しかし、この程度の関連性では将来予測はできません。

まずは、ランダムウォークに対してモデルを組んでみましょう。

model.RW <- auto.arima(
random.walk,
ic=”aic”,
trace=T,
stepwise=F,
approximation=F
)

結果はこちら。

> model.RW
Series: random.walk
ARIMA(0,1,0)

sigma^2 estimated as 0.9405: log likelihood=-553.92
AIC=1109.83 AICc=1109.84 BIC=1113.82

ARIMA(0,1,0)、すなわち、一回差分を取るという作業をしただけということです。差分を取っただけでARモデルもMAモデルも何の係数も推定できていません。

予測結果を出してみます。

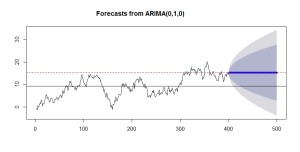
plot(forecast(model.RW, h=100), flwd=5)
abline(h=mean(random.walk))
abline(h=random.walk[400], col=2, lty=2)

ランダムウォークの予測結果は、「明日は今日と同じ」というものです。
黒い線は前回同様データの平均値ですが、予測値はそれとは大きく異なっています。
赤い点線は、400番目、すなわち最後に得られたデータの大きさを表しています。予測値はこれと全く等しいですね。

データを長いこと取っているといつかはもともとの平均値に戻ってくるような性質を平均回帰と言います。
ふだん60点くらいしかテストで点を取れない人がたまにまぐれで90点とか30点とかとっても、長いスパンで見たら60点にまた戻ってくる、という状況ですね。

和分過程でない、定常過程ならば平均に回帰します。
しかし、ランダムウォークのような和分過程は平均に回帰しません。これから増えるか減るか全くわからんということです。
だから予測区間もどんどん広がっていっていますね。

予測をする際、データが和分過程かどうかで結果が相当変わってくるということはぜひご銘記下さい。