時系列分析_実践編

最終更新:2016年1月24日

Rを用いた時系列解析の実践例を載せます。
Rを使えばARIMAもSARIMAもサクッと一瞬で計算できますよ。
時系列解析って何？　という方は
・時系列解析_理論編
・時系列解析_ホワイトノイズとランダムウォーク
も参照してください。

スポンサードリンク

 

目次

１．使用データ
２．モデリングと予測　その1、和分過程でないデータ
３．モデリングと予測　その２、和分過程
４．モデリングと予測　その３、季節変動データ

 

１．使用データ

シミュレーションデータと、Rにもともと入っているサンプルデータを用います。

シミュレーションデータはこちら

set.seed(1)
d <- arima.sim(
n=400,
model=list(order=c(2,0,2), ar=c(0.5,0.4), ma=c(-0.5,0.3)),
sd=sqrt(1)
)

order=c(2, 0, 2)なので自己回帰(AR)モデルが２次で、移動平均(MA)モデルも２次であるシミュレーションデータを作りました。残りのはARモデルやMAモデルの係数とノイズの大きさの指定です。n=400なので、シミュレーションデータは400個作られることになります。

ARIMA(２,０,２）モデルが推定できれば正解です。こちらはARMA過程であって、和分過程ではありません。「定常過程」とも言われる安定した挙動を示します。
「定常過程」についての詳しい説明は参考文献をどうぞ。

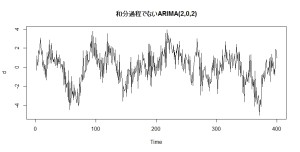
こんな形状をしています。

plot(d, main=”和分過程でないARIMA(2,0,2)”)

もう一つ、和分過程のデータも用意してみます。

set.seed(1)
dd <- arima.sim(
n=400,
model=list(order=c(2,1,2), ar=c(0.5,0.4), ma=c(-0.5,0.3)),
sd=sqrt(1)
)

さっきの和分過程で無いデータとは大分と違った挙動をすることを確かめます。

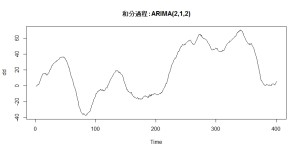
こんな形状をしています。さっきとはかなり異なっています。

plot(dd, main=”和分過程：ARIMA(2,1,2)”)

そして、季節的周期変動があるデータとして、Air Passengerというデータを用います。これは、月別国際空港路線総顧客数 （単位　千人）のデータで、時系列解析のサンプルデータとして割と有名なものです。

data<-ts(AirPassengers[1:132], start=c(1949,1), frequency=12)

AirPassengersのうち、最後の一年間はテスト用として省いておきました。最後の一年間をモデルを使って予測してみて、正しく予測できているかどうかを見極めます。

このプログラムの解説をすると、ts()で時系列データとして読み込むと言う指示を、AirPassengers[1:132]でAirPassengesr というデータにおける１～１３２番目のデータのみを用いると言う指示を。start=c(1949,1)で1949 年の単位1からスタートということを。frequency=12で 一単位は一年間の12分の一⇒要するに月単位データだと言うことを表します。だから、startは1949年の1月ということになります。

もし（Excelなど）手持ちのデータを時系列データとして読み込みたいのであればこのやり方が普通なのですが、AirPassengersというデータはもともと時系列データとしてRに保存されています。
時系列データであれば、window()関数を使えば簡単に最後の一年間だけ削除することが可能です。

data <- window(AirPassengers, end=c(1959, 12))

こちらの方が分かり易いですね。データにおいて、最後を１９５９年の１２月までにしたわけです。元データは１９６０年の１２月までデータがあるので、一年分をこれで取り除けたと。

データの形式に応じて使い分けてください。

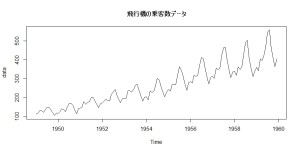
グラフはこちら

plot(data, main=”飛行機の乗客数データ”)

 

２．モデリングと予測　その１、和分過程で無いデータ

早速forecastパッケージを使ってモデリングしてみます。パッケージforecastをインスト－ルしてから以下を実行するだけで完成。

library(forecast)

model.1 <- auto.arima(
d,
ic=”aic”,
trace=T,
stepwise=F,
approximation=F,
start.p=0,
start.q=0,
start.P=0,
start.Q=0
)

あえて縦に長く書いてみたのですが、指定するのがやや多いですね。
１行目から順番に、
・データの指定、
・情報量基準に何を使うか(今回はAIC)、
・「こう言うモデ ルを作ってみてAICを計算してみましたよ」という計算履歴の一覧をずらずらと表示させてねという指示
・計算をケチらないで、なるべくほとんどの次数の組み合わせを総当たりに計算してねという指示
・近似的な計算手法を使わないでね
・ARモデルの次数は０から順に増やしていってね
・MAモデルも次数は０から順に増やしていってね
・季節部分のARも同様
・季節部分のMAも同様

季節部分のARモデルってなんだか不思議な言い方ですね。
季節モデルでは、１２か月ごとにデータをとって、たとえば１月なら１月だけで「１月の影響力」を抽出してやります。で、その季節成分にもARIMAモデルを当てはめているわけです。だから季節成分のデータ数は、元のデータ数÷１２個しかありません。
2000年の1月の季節成分は1999年の1月の季節成分から予測できるだろうと考えているわけですね。2000年1月、2001年1月、2002年1月・・・2013年1月みたいにすれば14個のデータセットが作れて、この14個の季節成分においてもARIMAモデルを作るわけ。

結果はこうなります（traceは省略）

> model.1
Series: d
ARIMA(2,0,2) with zero mean

Coefficients:
ar1 　　　ar2 　　　ma1 　　　　ma2
0.4847 　0.3991　 -0.4895 　0.2915
s.e. 0.0853　 0.0832 　 0.0889 　 0.0728

sigma^2 estimated as 1.027: log likelihood=-573.72
AIC=1157.43 AICc=1157.58 BIC=1177.39

うまいこと、ARIMA(2,0,2)モデルを選択できました。ちなみに、たまに（というか、よく）本来のモデルとは別のモデルを 「もっとも良い」として引っ張ってきてしまいます。それだけ時系列モデルを正確に選ぶのは難しいということでしょうか？

モデルが「良い」モデルかどうかは、残差（予測値－実測値）がきれいにばらついているかどうかを確かめることによって、ある程度判断 できます。
要するに、予測値の方が実測値よりも常に大きいとかいうような系統的な誤差があれば失敗ということになります。また、残差に自己相関があれば、これはこ れでうまくモデリングできていないことになります。誤差はあくまでも、誤差らしくあるような状態が理想である訳。

tsdiag(model.1)

とすれば、こんなグラフが出てきます。

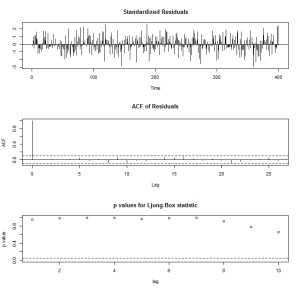
３つグラフが出てきますが、一番上が残差のプロット。２番目が残差の自己相関です。これはなるべく小さい方がよいです。３番目が残差が本当に「誤差らしい 誤差（ホワイトノイズ）」になっているかの検定プロットです。丸いぽつぽつが上の方にあって、青い線を下回らないようであれば、ホワイトノイズと見なすこ とができます。

最後に予測をしてみます。

forecast(model.1, level = c(50,95), h = 10)

結果はこちら

> forecast(model.1, level = c(50,95), h = 10)
Point Forecast　　 Lo 50　　　 Hi 50 　　　　Lo 95　　　　 Hi 95
401 　1.9577834 　1.27435577 　2.641211 　-0.02815271 　3.943720
402　 1.2923192　 0.60888372　 1.975755　 -0.69363975　 3.278278
403　 1.4077599　 0.57809577 　2.237424　 -1.00311706　 3.818637
404 　1.1981052　 0.33803368 　2.058177　 -1.30113105 　3.697341
405 　1.1425668 　0.23246153 　2.052672　 -1.50205987 　3.787194
406　 1.0319697　 0.09208583　 1.971854 　-1.69918896　 3.763128
407 　0.9561992　 -0.01202450　 1.924423　 -1.85731078　 3.769709
408　 0.8753329　 -0.11464335 　1.865309 　-2.00138649　 3.752052
409　 0.8058969　 -0.20268714 　1.814481　 -2.12489402　 3.736688
410　 0.7399671　 -0.28383077 　1.763765　 -2.23503281　 3.714967

level = c(50,95)とすると、９５％予測区間と、５０％予測区間が両方同時にもとまります。ｈ＝１０は、１０期先まで予測すると いう意味です。

プロットしてみます。
まずは直近の予測結果を返します。

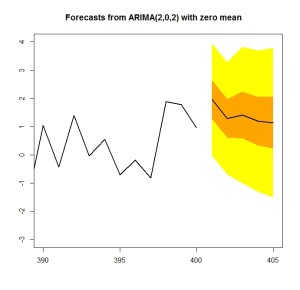
plot(
forecast(model.1, level = c(50,95), h = 5),
shadecols=c(“yellow”, “orange”),
fcol=1,
xlim=c(390, 405),
ylim=c(-3, 4),
lwd=2
)

しっかり予測してくれていますね。
では、長期予測をするとどうなるでしょうか。

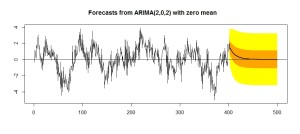
plot(
forecast(model.1, level = c(50,95), h = 100),
shadecols=c(“yellow”, “orange”),
fcol=1,
)
abline(h=mean(d))

ホワイトノイズとランダムウォークで説明したように、長期的には平均に回帰するだろうと考えているわけです。
ARIMAモデルで長期予測をしたいなら簡単ですね。平均値を出せばよい。

複雑な統計モデルを使っても、長期予測はあてにならないことを確認してください。

 

２．モデリングと予測　その２、和分過程

今度は 和分過程のモデリングをしてみます。

予測区間のとられ方がかなり変わるので、そこに注目すると特徴がよくわかります。

model.2 <- auto.arima(
dd,
ic=”aic”,
trace=T,
stepwise=F,
approximation=F
)

結果はこちら

> model.2
Series: dd
ARIMA(2,1,2)

Coefficients:
ar1　　　 ar2 　　　ma1 　　　ma2
0.4847 　0.3991 　-0.4895 　0.2915
s.e. 0.0853 　0.0832 　0.0889 　  0.0728

sigma^2 estimated as 1.027: log likelihood=-573.72
AIC=1157.43 AICc=1157.58 BIC=1177.39

今回もうまく推定できました。しかし、いつもこういくとは限りません。

たとえば、モデルを作るのに用いるデータを一体どれくらいの期間の長さを使えばいいのか、長すぎても短すぎても余り良くない……なんていうことを考えて行くとかなり難儀します。今回はそういう難しい話は無視して予測してしまいました。

今回は残差プロットは無視して、先に予測をしてみます。

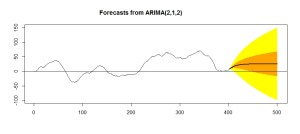
 plot(
forecast(model.2, level = c(50,95), h = 100),
shadecols=c(“yellow”, “orange”),
fcol=1
)

abline(h=mean(d))

時が経つにつれて、予測幅（９５％の確率でとりうる値の幅）がどんどん大きくなっていきます。これが和分過程の特徴です。ようするに、 精確な予測が難しくなっているわけです。

元々のデータのグラフの形も、和分過程で無いものと比べると、大分と違うことが見て取れると思います。

 

４．モデリングと予測　その３、季節変動データ

最後に、季節変動データの予測です。SARIMAモデルもauto.arimaで勝手に推定してくれるので、全部任せてしまうことに します。

model.Air <- auto.arima(
data,
ic=”aic”,
trace=T,
stepwise=T,
approximation=F,
allowdrift=F,
start.p=0,
start.q=0,
start.P=0,
start.Q=0,
)

 

結果はこちら

> model.Air
Series: data
ARIMA(1,1,0)(0,1,0)[12]

Coefficients:
ar1
-0.2431
s.e. 0.0894

sigma^2 estimated as 108.9: log likelihood=-447.95
AIC=899.9 AICc=900.01 BIC=905.46

こちらも1次の和分過程となりました。増加や減少トレンドは、和分過程としてモデリングすると上手く表すことができます。

ここで、いままでは省略していたtraceのけっかにややおかしなところが見られます。
traceはauto.arima関数を実行したときにtrace=T指定をしておくと勝手に出てくる出力ですが、このような結果になっているはずです。

ARIMA(0,1,0)(0,1,0)[12] : 905.0652
ARIMA(0,1,0)(0,1,0)[12] : 905.0652
ARIMA(1,1,0)(1,1,0)[12] : 900.8231
ARIMA(0,1,1)(0,1,1)[12] : 901.7211
ARIMA(1,1,0)(0,1,0)[12] : 899.9021
ARIMA(1,1,0)(0,1,1)[12] : 901.0524
ARIMA(1,1,0)(1,1,1)[12] : 1e+20
ARIMA(2,1,0)(0,1,0)[12] : 901.3376
ARIMA(1,1,1)(0,1,0)[12] : 900.9716
ARIMA(2,1,1)(0,1,0)[12] : 902.9668

Best model: ARIMA(1,1,0)(0,1,0)[12]

ひとつだけ、AICのあたいが1e+20という意味不明なことになってしまっていますね。
stepwise＝Fにしてもすべてのモデルを総当たりに計算できているわけではないのは、こういう状況がよく生じるためです。

こういうときは、気になるモデルのAICを手作業で計算してやりましょう。

arima(data,
order=c(1,1,0),
seasonal=list(order=c(1,1,1))
)

arima(data,
order=c(1,1,0),
seasonal=list(order=c(0,1,0))
)

一つ目のarimaはAICが算出されていない次数のARIMAモデル作成を指示していて、二つ目は、今回ベストモデルとして選ばれた時数を使っています。関数によってAICの計算方法が違ってたりするので、AICを比較する際は同じ関数で計算されたAIC同士で比較する癖をつけたほうが良いと思います。

で、結果だけ書くとauto.arimaの結果を使って問題ないことがわかりました。
このベストモデルを使って予測を行います。

予測と実際の結果を合わせてプロットしてみます。

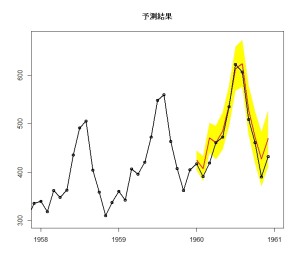
plot(
forecast(model.Air, level = c(95), h = 12),
shadecols=c(“yellow”, “orange”),
fcol=2,
flwd=2,
xlim=c(1958, 1961),
ylim=c(300, 675),
type=”o”,
xaxt = “n”,
main=”予測結果”
)

lines(AirPassengers, type=”o”, lwd=2)

Axis(
at = seq(1958, 1961),
side = 1
)

 そのままだとx軸がやや変な感じになってしまったので、plotにおいてxaxt = “n”を指定してx軸を消去した後にAxis関数を使って別個にx軸を設定しなおしました。

まぁまぁうまく予測できていることが分かります。

 

参考文献

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)   このサイトで時系列解析関連の記事を書く際は必ず参照している本です。 時系列解析の基本となる考え方から始めて、モデルの詳しい説明まで載っています。 今、時系列解析を学びたいと思った方はこの本から入ると良いでしょう。

Rによる時系列分析入門   Rを使ってARIMAモデルを推定する方法がとても丁寧に乗っています。 forecastパッケージは使っていないのでコードをそのまま使うのは無理かもしれませんが、時系列解析の基礎を学ぶには良いと思います。

現場ですぐ使える時系列データ分析 ~データサイエンティストのための基礎知識~   大変読みやすい、Rによる時系列解析の入門書です。 ARIMAモデルが載っていないのは残念ですが、ARモデルの説明はあります。 GARCHモデルなどより進んだモデルのことも載っています。

 

書籍以外の参考文献

Package ‘forecast’　説明書（PDF)
http://cran.r-project.org/web/packages/forecast/forecast.pdf

時系列グラフの設定はこちらのサイト様に詳しく書かれていました。
もうかつ丼でいいよな　時系列プロット

スポンサードリンク